https://hackaday.io/post/30838

https://en.m.wikipedia.org/wiki/Hackaday

http://www.instructables.com/id/How-to-Make-12v-Battery-Charge/

In inferential statistics, the term “null hypothesis” is a general statement or default position that there is no relationship between two measured phenomena, or no association among groups.^[1] Rejecting or disproving the null hypothesis—and thus concluding that there are grounds for believing that there is a relationship between two phenomena (e.g. that a potential treatment has a measurable effect)—is a central task in the modern practice of science; the field of statistics gives precise criteria for rejecting a null hypothesis.

The null hypothesis is generally assumed to be true until evidence indicates otherwise. In statistics, it is often denoted H₀ (read “H-nought”, “H-null”, or “H-zero”).

The concept of a null hypothesis is used differently in two approaches to statistical inference. In the significance testing approach of Ronald Fisher, a null hypothesis is rejected if the observed data are significantly unlikely to have occurred if the null hypothesis were true. In this case the null hypothesis is rejected and an alternative hypothesis is accepted in its place. If the data are consistent with the null hypothesis, then the null hypothesis is not rejected (i.e., accepted). In neither case is the null hypothesis or its alternative proven; the null hypothesis is tested with data and a decision is made based on how likely or unlikely the data are. This is analogous to a criminal trial, in which the defendant is assumed to be innocent (null is not rejected) until proven guilty (null is rejected) beyond a reasonable doubt (to a statistically significant degree).

In the hypothesis testing approach of Jerzy Neyman and Egon Pearson, a null hypothesis is contrasted with an alternative hypothesis and the two hypotheses are distinguished on the basis of data, with certain error rates.

Proponents of each approach criticize the other approach. Nowadays, though, a hybrid approach is widely practiced and presented in textbooks. The hybrid is in turn criticized as incorrect and incoherent—for details, see Statistical hypothesis testing.

Statistical inference can be done without a null hypothesis, by specifying a statistical model corresponding to each candidate hypothesis and using model selection techniques to choose the most appropriate model.^[2](The most common selection techniques are based on either Akaike information criterion or Bayes factor.

Source: Null hypothesis – Wikipedia

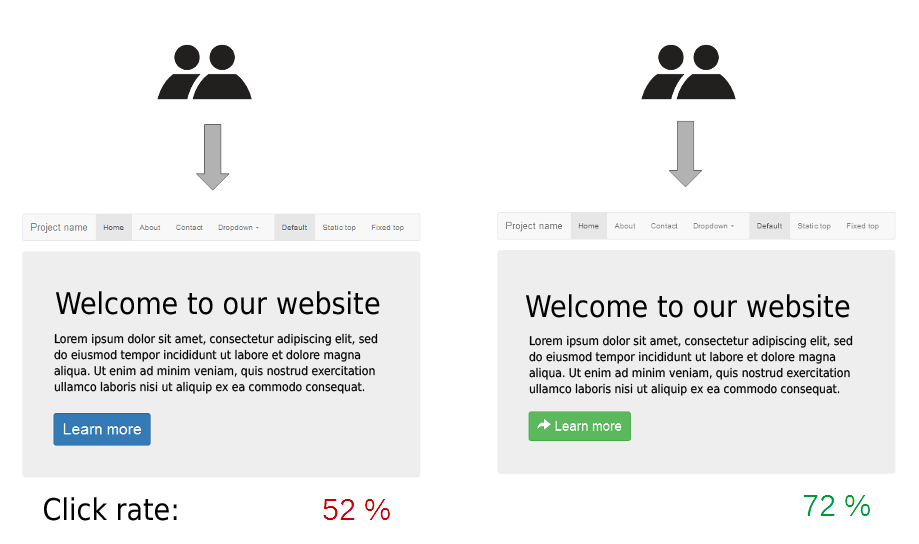
In marketing and business intelligence, A/B testing is a term for a randomized experiment with two variants, A and B, which are the control and variation in the controlled experiment.^[1] A/B testing is a form of statistical hypothesis testing with two variants leading to the technical term, two-sample hypothesis testing, used in the field of statistics. Other terms used for this method include bucket tests and split-run testing. These terms can have a wider applicability to more than two variants, but the term A/B testing is also frequently used in the context of testing more than two variants. In online settings, such as web design (especially user experience design), the goal of A/B testing is to identify changes to web pages that increase or maximize an outcome of interest (e.g., click-through rate for a banner advertisement). Formally the current web page is associated with the null hypothesis. A/B testing is a way to compare two versions of a single variable typically by testing a subject’s response to variable A against variable B, and determining which of the two variables is more effective.^[2]

As the name implies, two versions (A and B) are compared, which are identical except for one variation that might affect a user’s behavior. Version A might be the currently used version (control), while version B is modified in some respect (treatment). For instance, on an e-commerce website the purchase funnel is typically a good candidate for A/B testing, as even marginal improvements in drop-off rates can represent a significant gain in sales. Significant improvements can sometimes be seen through testing elements like copy text, layouts, images and colors,^[3]but not always. The vastly larger group of statistics broadly referred to as multivariate testing or multinomial testing is similar to A/B testing, but may test more than two different versions at the same time and/or has more controls, etc. Simple A/B tests are not valid for observational, quasi-experimental or other non-experimental situations, as is common with survey data, offline data, and other, more complex phenomena.

A/B testing has been marketed by some as a change in philosophy and business strategy in certain niches, though the approach is identical to a between-subjects design, which is commonly used in a variety of research traditions.^[4][5][6] A/B testing as a philosophy of web development brings the field into line with a broader movement toward evidence-based practice. The benefits of A/B testing are considered to be that it can be performed continuously on almost anything, especially since most marketing automation software now, typically, comes with the ability to run A/B tests on an on-going basis. This allows for updating websites and other tools, using current resources, to keep up with changing trends.

Source: A/B testing – Wikipedia

Mario Del Monaco

From Wikipedia, the free encyclopedia

Mario Del Monaco
Born	27 July 1915 Florence, Italy
Died	16 October 1982 (aged 67) Mestre, Italy
Occupation	Opera singer (tenor)
Years active	1940 – 1975

Mario Del Monaco (27 July 1915 – 16 October 1982)^[1] was an Italian operatic tenor who earned worldwide acclaim for his powerful voice.

Source: Mario Del Monaco – Wikipedia