\sloppy
1 Static Maximal Flow (Ford & Fulkerson Textbook)
1.1 Networks
A directed network or directed linear graph G = [N;A] consist of a collection N of elements x, y, ..., together with a subset A of the ordered pairs (x, y) of elements taken form N.
Let x1, x2, ..., xn (n ≥ 2) be a sequence of distinct nodes of a network such that (xi, xi + 1) is an arc, for each i = 1, ..., n − 1. Then the sequence of nodes and arcs
is called chain.
Incidence matrix:
(s, x)
(s, y)
(x, y)
(y, x)
(x, t)
(y, t)
s
1
1
0
0
0
0
x
− 1
0
1
− 1
1
0
y
0
− 1
− 1
1
0
1
t
0
0
0
0
− 1
− 1
\mathchoiceA(x)A(x)A(x)A(x) - „After x”
A(x) = {y ∈ N|(x, y) ∈ A}
\mathchoiceB(x)B(x)B(x)B(x)- „Before x”
B(x) = {y ∈ N|(y, x)) ∈ A}
e.g. A(s) = {x, y} B(s) = ∅
1.2 Flows in networks
c(x, y) - Capacity of arc (x, y) ∈ A
Let s and t be distinguished nodes of N . A static flow of value v from s to t in [N;A] is function from A to non-negative reals that satisfies the linear equations and inequalities
We call s source, t the sink, and other nodes intermediate. Thus the net flow out of x is defined to be:
⎲⎳y ∈ A(x)f(x, y) − ⎲⎳y ∈ B(x)f(y, x)
then the equations 2↑ may be verbalized by saying that the net flow out of the source is v, the flow out of the sing is − v, whereas the net flow out of an intermediate node is zeor. The eqution of latter kind will be called a conservation equation.
The value of the flow in 2↑ is 3.
the static maximal flow problem is that of maximizing the variable v subject to the flow constraints 2↑ and 3↑.
Suppose that A1, ...Am is enumeration of the arcs of a network, the arc Ai having capacity c(Ai); and let \mathchoiceC1, ..., CnC1, ..., CnC1, ..., CnC1, ..., Cn be list of all directed chains from s to t. Form the m by n incidence matrix (aij) of arcs versus chains by defining
Now let h be a function from the set of chains C1, ..., Cn to non-negative reals that satisfies the inequalities
We refer to h as flow from s to t in arc-chain form, and call h(Cj) a chain flow or the flow in chain Cj. The value of h is
When we need to distinguish the two notions of a flow from s to t thus far introduced, we shall call a function f from the set of arcs to non-negative reals whic satisfies 2↑ and 3↑ for some v, a flow from s to t in node-arc form. There will usually be no need for the distinction, since we shall work almost exclusively with node-arc flows after this section.
Let explore the relationship between these two formulations of the intuitive notion of a flow. Suppose that x1, ..., xl is a list of the nodes, and let \mathchoice(bki), k = 1, ..., l, i = 1, ..., m(bki), k = 1, ..., l, i = 1, ..., m(bki), k = 1, ..., l, i = 1, ..., m(bki), k = 1, ..., l, i = 1, ..., m, be the node-arc incidence matrix introduced earlier. Thus
(7)
bki
= ⎧⎪⎨⎪⎩
1
if Ai = (xk, y),
− 1
if Ai = (y, xk)
0
otherwise.
Then
bkiaij = ⎧⎪⎨⎪⎩
1
if Ai = (xk, y), and Ai ∈ Cj
− 1
if Ai = (y, xk), and Ai ∈ Cj
0
otherwise.
it follows that
If h is a flow from s to t in arc-chain form, and if we define:
(9) \mathchoicef(Ai) = n⎲⎳j = 1aijh(Cj), i = 1, ..., mf(Ai) = n⎲⎳j = 1aijh(Cj), i = 1, ..., mf(Ai) = n⎲⎳j = 1aijh(Cj), i = 1, ..., mf(Ai) = n⎲⎳j = 1aijh(Cj), i = 1, ..., m
f(Ai) ≤ c(Ai)
and by 8↑,
\strikeout off\uuline off\uwave off
m⎲⎳i = 1bkif(Ai) = m⎲⎳i = 1n⎲⎳j = 1bkiaijh(Cj) = n⎲⎳j = 1(m⎲⎳i = 1bkiaij)h(Cj) = ⎧⎪⎨⎪⎩
n⎲⎳j = 1h(Cj)
if xk = s,
− n⎲⎳j = 1h(Cj)
if xk = t,
0
otherwise.
There are various vays of obtaining such an arc-chain flow h from a given node-arc flow f. One way is as follows. Define
(10) \mathchoiceh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., n
where
f1(Ai) = f(Ai)
f2(Ai) = f(Ai) − ai1h(C1)
f3(Ai) = f(Ai) − ai1h(C1) − ai2h(C2)
...
fn + 1(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ... − ainh(Cn)
Не ми е јасно зошто секвенцијално ги одзема протоците од другите патеки (ланци)? Тие може не се подредени.
f2(Ai) = f(Ai) − ai1h(C1)
f3(Ai) = f(Ai) − ai1h(C1) − ai2h(C2)
...
fn + 1(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ... − ainh(Cn)
Не ми е јасно зошто секвенцијално ги одзема протоците од другите патеки (ланци)? Тие може не се подредени.
It follows that fj + 1 is a node-arc flow from s to t having value v(fj + 1) = v − ∑jp = 1h(Cp), since
m⎲⎳i = 1bkifj + 1(Ai) = m⎲⎳i = 1bkif(Ai) − m⎲⎳i = 1j⎲⎳p = 1bkiaiph(Cp) = ⎧⎪⎨⎪⎩
v − j⎲⎳p = 1h(Cp)
if xk = s
− v + j⎲⎳p = 1h(Cp)
if xk = t
0
otherwise
Moreover, fj + 1(Ai) ≤ fj(Ai), all Ai , and fj + 1(Ai) = 0 for some Ai ∈ Cj. Hence the node-arc flow fn + 1 vanishes on some arc of every chain form s to t. This implies that v(fn + 1) ≤ 0, as the following lemma shows.
Lemma 2.1.
If f is a node-arc flow from s to t having value v(f) > 0 , then there is a chain form s to t such that f > 0 on all arcs of this chain.
Proof.
Let X be the set of nodes defined recursively by the rules
(a) s ∈ X
(b) if x ∈ X and if f(x, y) > 0 then y ∈ X.
We assert that t ∈ X. For, suppose not. Then, summing the equations 2↑ over x ∈ X , and noting cancellations, we have
v(f) = ⎲⎳
x ∈ X
y∉X
[f(x, y) − f(y, x)]
But by (b), if (x, y) is an arc with x ∈ X, y∉X then f(x, y) = 0. This and the last displayed equation contradict v(f) > 0. Thus t ∈ X. But for any x ∈ X, the definiton of X shows that there is a chain form s to x such that f > 0 on arcs of this chain. Hence there is a chain form s to t with this property.
It follows from the lemma that the value of fn + 1 is non-positive, that is
v(fn + 1) = v − \oversetv(h)n⎲⎳p = 1h(Cp) ≤ 0
consequently v(h) ≥ v. This proves
Theorem 2.2.
If h is an arc-chain flow from s to t, then f defined by 9↑ is a node-arc flow from s to t and v(f) = v(h). On the other hand, if f is a node-arc flow from s to t, then h defined by 10↑ and 11↑ is an arc-chain flow from s to t, and v(h) ≥ v(f).
Не баш ја контам!!
A consequence of Theorme 2.2 is that it is immaterial wheter the maximal flow problem is formulated in terms of the node-arc incidence matrix or the arc-chain incidence matrix. Thus, for example, since arcs of the form (x, s) or (t, x) can be deleted from A without changing the list of chains from s to t we may always suppose in either formulation of the maximal flow problem that all source arcs points out from the source and all sink arcsk point into the sink. (For such networks, one has v(h) = v(f) in the second part of Theorem 2.2 as well as the first part.)
A function h defined from f as in 10↑ and 11↑ will be termed a chain decomposition of f. A chain decomposition of f will in general depend on the ordering of the chains.
For example, if in 1↑ we take f = 1 on all arcs, and take C1 = (s, x, t), C2 = (s, y, t), C3 = (s, x, y, t), C4 = (s, y, x, t) then h(C1) = h(C2) = 1,
h(C3) = h(C4) = 0. But, examining the chains in reverse order would lead to \strikeout off\uuline off\uwave offh(C1) = h(C2) = 0, h(C3) = h(C4) = 1\begin_inset Separator latexpar\end_inset
\mathchoiceh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., nh(Cj) = minAi ∈ Cjfj(Ai), j = 1, ..., n
h(C1) = minf1(Ai); h(C2) = minf2(Ai); h(C3) = minf3(Ai); h(C4) = minf4(Ai);
fj(Ai) = f(Ai) − ∑j − 1p = 1aiph(Cp) j = 1, 2, ..., n + 1
f1(Ai) = f(Ai); f2(Ai) = f(Ai) − ai1h(C1); f3(Ai) = f(Ai) − ai1h(C1) − ai2h(C2); f4(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ai3h(C3);
f5(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ai3h(C2) − ai4h(C2)
fj|Ai A1 = (sx) A2 = (sy) A3 = (xy) A3 = (yx) A5 = (xt) A6 = (yt) h(Cj) f1(Ai) 1 1 1 1 1 1 1 f2(Ai) 0 1 1 1 0 1 0 f3(Ai) 0 1 1 1 0 1 0 f4(Ai) 0 1 1 1 0 1 0 f5(Ai) 0
Reverse order:
C1 = (s, y, x, t), C2 = (s, x, y, t), C3 = (s, y, t), C4 = (s, x, t);
fj|Ai A1 = (sx) A2 = (sy) A3 = (xy) A3 = (yx) A5 = (xt) A6 = (yt) h(Cj) f1(Ai) 1 1 1 1 1 1 1 f2(Ai) 1 0 1 0 0 1 0 f3(Ai) f4(Ai) f5(Ai)
h(C1) = minf1(Ai); h(C2) = minf2(Ai); h(C3) = minf3(Ai); h(C4) = minf4(Ai);
fj(Ai) = f(Ai) − ∑j − 1p = 1aiph(Cp) j = 1, 2, ..., n + 1
f1(Ai) = f(Ai); f2(Ai) = f(Ai) − ai1h(C1); f3(Ai) = f(Ai) − ai1h(C1) − ai2h(C2); f4(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ai3h(C3);
f5(Ai) = f(Ai) − ai1h(C1) − ai2h(C2) − ai3h(C2) − ai4h(C2)
fj|Ai A1 = (sx) A2 = (sy) A3 = (xy) A3 = (yx) A5 = (xt) A6 = (yt) h(Cj) f1(Ai) 1 1 1 1 1 1 1 f2(Ai) 0 1 1 1 0 1 0 f3(Ai) 0 1 1 1 0 1 0 f4(Ai) 0 1 1 1 0 1 0 f5(Ai) 0
Reverse order:
C1 = (s, y, x, t), C2 = (s, x, y, t), C3 = (s, y, t), C4 = (s, x, t);
fj|Ai A1 = (sx) A2 = (sy) A3 = (xy) A3 = (yx) A5 = (xt) A6 = (yt) h(Cj) f1(Ai) 1 1 1 1 1 1 1 f2(Ai) 1 0 1 0 0 1 0 f3(Ai) f4(Ai) f5(Ai)
From the computational point of view, one would cetainly suppose the node-arc formulation of the maximal flow problem to be preferable for most networks, since the number of chains from s to t is likely to be large compared to numebr of nodes or the number of arcs. A computing procedure that required as a first sep the enumeration of all chains form s to t would be of little value.
1.3 Notation
To simplify the notation, we adopt the following conventions. If X and Y are subsets of N, let (X, Y) denote the set of all arcs that lead form x ∈ X to y ∈ Y; and, for any function g from A to reals, let
Similarly, when dealing with a function h defined on the nodes of N, we put
⎲⎳x ∈ Xh(x) = h(X)
We customarly denote a set consisting of one element by its single element. Thus if X contains the single node x, we write (x, Y), g(x, Y) and so on.
Sets unions, intersections, and differences will be denoted by ∪, ∩, and − , respectively. We use ⊆ for set inclusion, and ⊂ for proper inclusion. Complements of sets will be denoted by barring the appropriate symbol. For instance, the complement of X in N is X = N − X.
Thus, if X, Y, Z ⊆ N then:
Hence if Y and Z are disjoint,
g(X, Y∪Z) = g(X, Y) + g(X, Z)
g(Y∪Z, X) = g(Y, X) + g(Z, X)
Notice that
(B(x), x) = (N, x)
(x, A(x)) = (x, N),
and
g(N, X) = ⎲⎳x ∈ Xg(N, x) = ⎲⎳x ∈ Xg(B(x), x)
g(X, N) = ⎲⎳x ∈ Xg(x, N) = ⎲⎳x ∈ Xg(x, A(x))
1.4 Cuts
Progress toward a solution of maximal network flow problem is made with the recognition of the importance of certain subsets of arcs, which we shall call cuts. A cut S in [N;A] separating s and t is a set of arcs (X, X) where s ∈ X , t ∈ X. The capacity of the cut (X, X) is c(X, X).
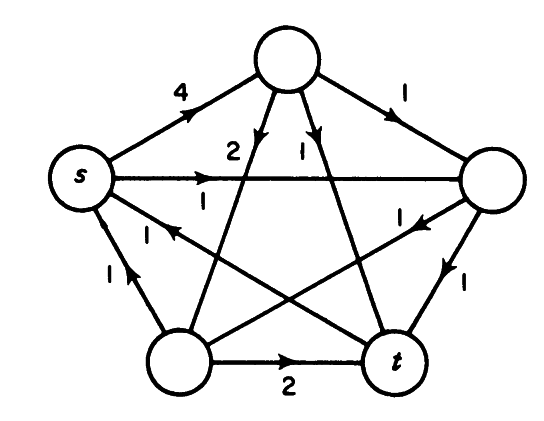
For example the set of arcs S = {(s, y), (x, y), (x, t)} with X = {s, x} is a cat in the network of 1↑ separating s and t.
Notice that any chain from s to t must contain some arc of every cut (X, X). For let x1, x2, ..., xn be a chain with x1 = s, xn = t . Since x1 ∈ X, xn ∈ X there is an xi (1 ≤ i < n) with xi ∈ X, xi + 1 ∈ X. Hence the arc (xi, xi + 1) is member of the cut (X, X). It follows that if all arcs of a cut were deleted from the network there would be no chain from s to t and the maximal flow value for the new network would be zero.
Затоа во Figure 15.4 од EIT ги собираат капацитетите на поединечните аркови од cut-от за да го добие максиманиот проток. Доколку секој од патеките би коирстела само еден од арковите од cut-от јасно е зошто вкупниот проток е сума од капацитетите на тие поединечни аркови.
Since a cut blocks all chains form s to t, it is intuitively clear (and indeed obvious in arc-chain version of the problem) that the value v of a flow f cannot exceed the capacity of any cut, a fact that we now prove from 2↑ and 3↑.
Let f be flow from s to t in network [N;A], and let f have value v. If (X, X) is a cut separating s and t, then
(15) \mathchoicev = f(X, X) − f(X, X) ≤ c(X, X)v = f(X, X) − f(X, X) ≤ c(X, X)v = f(X, X) − f(X, X) ≤ c(X, X)v = f(X, X) − f(X, X) ≤ c(X, X)
Proof.
The equality of 15↑ was actually proved in Lemma 2.1. We reporve it here, using the notation introduced in preceding section. Since f is a flow, f satisfies the equations
f(s, N) − f(N, s) = v
f(x, N) − f(N, x) = 0
x ≠ s, t
f(t, N) − f(N, t) = − v
Now sum these equations over x ∈ X. since s ∈ X and t ∈ X , the result is
v = ⎲⎳x ∈ X(f(x, N) − f(N, x)) = f(X, N) − f(N, X)
Writing N = X∪X in this equality yields
v = f(X, X∪X) − f(X∪X, X) = \cancelf(X, X) + f(X, X) − \cancelf(X, X) − f(X, X)
thus verifying the equality in 15↑. Since f(X, X) ≥ 0 and f(X, X) ≤ c(X, X) by virtue of 3↑, the inequality of 15↑ follows immediately.
In words, the equality 15↑ states that the value of a flow from s to t is equal to the net flow across any cut separating s and t.
1.5 Maximal flow
We arа now in position to state and prove the fundamental result concerning maximal network flow.
For any network the maximal flow value from s to t is equal to the minimum cut capacity of all cuts separating s and t. Before proving Theorem 5.1, we illustrate it with an example. Consider the network of 1↑ with capacity function c and flow f as indicated in 3↓, c(x, y) be the first member of the pair of numbers written
adjacent to arc (x, y) and f(x, y) the second. Here the flow value is 3. Since the cut composed of arcs (s, x), (y, x) and (y, t) also has capacity 3, it follows from Lemma 4.1 that the flow is maximal and the cut minimal.
Да го најдам капацитетот на cut-от:
(s, x), (y, x) and (y, t)
X = (s, y) X = (x, t)
(s, x), (y, x) and (y, t)
X = (s, y) X = (x, t)
f(X, X) = ⎲⎳i ∈ s, y ⎲⎳j ∈ x, tf(i, j) = f(s, x) + f(y, x) + f(y, t) = 3
f(X, X) = ⎲⎳i ∈ x, t ⎲⎳j ∈ s, yf(i, j) = 0
v = f(X, X) − f(X, X) = 3 − 0 = 3 ≤ c(X, X)
By Lemma 4.1 it suffices to establish the existence of a flow f and a cut (X, X) for which equality of flow value and cut capacity holds. We do this by taking a maximal flow f (clearly such exists) and defining, in terms of f, a cut (X, X) such that
f(X, X) = c(X, X)
f(X, X) = 0
so the equality holds throughout 15↑.
Thus let f be a maximal flow. Using f, define the set X recurively as follows:
(a) \mathchoices ∈ Xs ∈ Xs ∈ Xs ∈ X;
(b) if x ∈ X and f(x, y) < c(x, y), then y ∈ X;
if x ∈ X and f(y, x) > 0 then y ∈ X.
На пример во примерот од 3↑
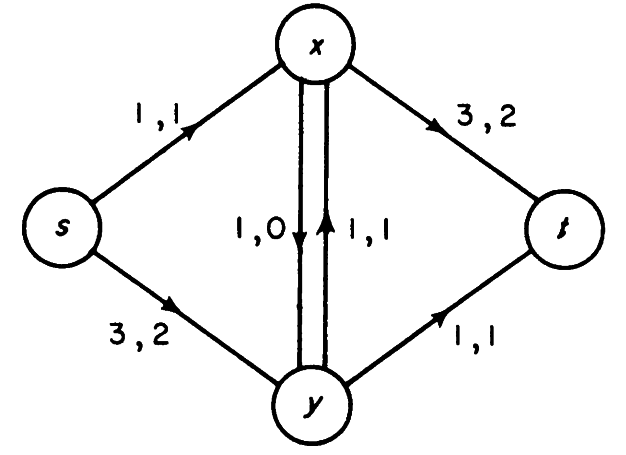

(s, x), (y, x) and (y, t)
X = (s, y) X = (x, t)
Да ги добијам рекурзивно:
let x = s ∈ X f(x, y) = f(s, x) > 0 → x ∈ X (a) f(x, y) = f(s, y) > 0 → y ∈ X
——————————————————————————–————————–
let x = y ∈ X f(x, y) = f(y, s) < 0 \mathchoicef(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)
X = (s, y) X = (x, t)
Да ги добијам рекурзивно:
let x = s ∈ X f(x, y) = f(s, x) > 0 → x ∈ X (a) f(x, y) = f(s, y) > 0 → y ∈ X
——————————————————————————–————————–
let x = y ∈ X f(x, y) = f(y, s) < 0 \mathchoicef(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)f(x, y) = f(y, x) > 0 → x ∈ X (b)
let x = x ∈ X \mathchoicef(x, y) = f(y, x) > 0 → y ∈ X (a)f(x, y) = f(y, x) > 0 → y ∈ X (a)f(x, y) = f(y, x) > 0 → y ∈ X (a)f(x, y) = f(y, x) > 0 → y ∈ X (a); f(x, y) = f(t, x) < 0; \strikeout off\uuline off\uwave offf(x, y) = f(s, x) < 0\uuline default\uwave default
x = s; f(y, x) = f(x, s) < 0 → x∉X f(y, x) = f(y, s) < 0 → y∉X
(a) → x = x; f(y, x) = f(s, x) < 0 → x∉X \mathchoicef(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ X f(y, x) = f(t, x) < 0 → t∉X
(b) → x = y; \mathchoicef(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉X \mathchoicef(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ X f(y, x) = f(t, y) < 0 → t∉X
Изгледа треба во (b) двата услови да бидат исполнети барем еднаш. Гледаш x ∈ X не е исполнет ниту еднаш во (b).
Можеби вака е алгоритамот. Откако го добив (b) сега претпоставувам во вторито чекор дек x = y па штом резултатот води да добијам дека s ∈ X што беше иницијалната претпоставка тоа да е доказ дека навистина y ∈ X.
(a) → x = x; f(y, x) = f(s, x) < 0 → x∉X \mathchoicef(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ Xf(y, x) = f(y, x) > 0 → y ∈ X f(y, x) = f(t, x) < 0 → t∉X
(b) → x = y; \mathchoicef(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉Xf(y, x) = f(x, y) = 0 → x∉X \mathchoicef(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ Xf(y, x) = f(s, y) > 0 → s ∈ X f(y, x) = f(t, y) < 0 → t∉X
Изгледа треба во (b) двата услови да бидат исполнети барем еднаш. Гледаш x ∈ X не е исполнет ниту еднаш во (b).
Можеби вака е алгоритамот. Откако го добив (b) сега претпоставувам во вторито чекор дек x = y па штом резултатот води да добијам дека s ∈ X што беше иницијалната претпоставка тоа да е доказ дека навистина y ∈ X.
We assert that t ∈ X. For, suppose not. It then follows from the definition of X that there is a path from s to t, say
s = x1x2, .., xn = t
having the property that for all forward arcs (xi, xi + 1) of the path,
f(xi, xi + 1) < c(xi, xi + 1)
whereas for all reverse arcs (xi + 1, xi) of the path
f(xi + 1, xi) > 0
Let ϵ1 be the minimum of c − f taken over all froward arcs of the path, ϵ2 the minimum of f taken over all reverse arcs, and let ϵ = min(ϵ1, ϵ2) > 0. Now alter the flow f as follows: increase f by ϵ on all forward arcs of the path, and decrease f by ϵ on all reverse arcs. It is easily checked that the new function thus defined is a flow from s to t having value v + ϵ. But then f is not maximal, contry to our assumption, and thus t ∈ X.
Consequently (X, X) is cut separating s and t. Moreover, form definiton of X, it follows that
f(x, x) = c(X, X), for (x, x) ∈ (X, X)
f(x, x) = 0, (x, x) ∈ (X, X),
since otherwise x would be in X. Thus
f(X, X) = c(X, X) f(X, X) = 0
so the equality holds in 15↑.
Several corollaries can be gleaned form Lemma 4.1, Theorem 5.1 and its proof.
We shall call a path from s to t flow augmenting path with respect to a flow f provided that f < c on forward arcs of the path, and f > 0 on reverse arcs of the path. Then we have,
A flow f is maximal if and only if there is no flow augmenting with respect to f.
If f is maximal, then clearly no flow augmenting path exists. Suppose, conversely, that no flow augmenting path exists. Then the set X defined recursively using f as in the proof of Theorem 5.1 cannot contain the sink t. Hence, as in the proof of Theorem 5.1, (X, X) is a cut separating s and t having capacity equal to the value of f. Consequenlty f is maximal.
Corollary 5.2 is of fundamental importance in the sudi of networks flows. It says, in essence, that in order to increase the value of a flow it suffices to look for improvements of a very restricted kind.
We say that an arc (x, y) is saturated with respect to flow f if f(x, y) = c(x, y) and is flowless with repsect to f if f(x, y) = 0. Thus an arc that is both saturated and flowless has zero capacity. Corollary 5.3 characterizes a minimal cut in terms of these notions.
A cut (X, X) is minimal if and only if every maximal flow f saturates all arcs of (X, X) whereas all arcs of (X, X) are flowless with respect to f.
Види 2↑ ќе видиш практично дека е ова вака!!!
Let (X, X) and (Y, Y) be minimal cuts. Then (X∪Y, X∪Y) and (X∩Y, X∩Y) are also minimal cuts.
(X∪Y, X∪Y) = (X, X∪Y) + (Y, X∪Y) − (X∩Y, X∪Y)
X∪Y = X + Y − X∩Y = N − X + \cancelN − Y − \cancelN + X∩Y = N − XUY
X∪Y = X + Y − X∩Y = N − X + \cancelN − Y − \cancelN + X∩Y = N − XUY
The following theorem shows that the minimal cut (X, X) sigled out in the proof in Theorem 5.1 does not, in actuality depend on the maximal flow f.
Let (Y, Y) be any minimal cut, let f be a maximal flow, and let (X, X) be the minimal cut defined relative to f in the proof of Theorem 5.1. Then X ⊆ Y.
Suppose that X is not included in Y. Then X∩Y ⊂ X , and (X∩Y, X∩Y) is minimal cut by Corrolary 5.4. Let x be a node in X that is not in X∩Y. Since x ∈ X and x ≠ s, there is a path form s to x , say s = x1, x2, ...xk = x such that each forward arc of the path is unsaturated with respect to f, while each reverse arc carries positive flow. But since s ∈ X∩Y and x ∈ X∩Y, there is a paid xi, xi + 1(1 ≤ i < k) such that xi ∈ X∩Y, xi + 1 ∈ X∩Y. If (xi, xi + 1) is forward arc of the path, then f(xi, xi + 1) < c(xi, xi + 1), contradicting Corollary 5.3. Similarly if (xi + 1, xi) is reverse arc of the path, Corollary 5.3 is contradicted. Hence X ⊆ Y.
Thus if (Xi, Xi), i = 1, .., m, are all the minimal cuts separating source and sink, the set X defined relative to a particualr maximal flow in the proof of Theorem 5.1 is the intersection of all Xi and hence does not depend on the selection of the flow.
Although the minimal cut (X, X) was picked out in the proof of Theorem 5.1 by a recursive definition of the source set X, symetrically we could have generated a minimal cut (Y, Y) by defining its sink set Y in terms of a maximal flow f as follows:
(a’) t ∈ Y
(b’) if y ∈ Y and f(x, y) < c(x, y) then x ∈ Y;
if y ∈ Y and f(y, x) > 0 , then x ∈ Y.
Equivalently, one can think of reversing all arc orientations and arc flows, interchanging source and sink so that t becomes the source, s the sink, and then use the definition given in the proof of Theorem 5.1 to construct Y. Again, although its definiton is made relative to a particular maximal flow, the set Y does not actually depend on the selection, since Y is intersection of the sink sets Xi of all minimal cuts (Xi, Xi).
Using both definitions, we can state a criterion for uniquenes of a minimal cut.
Let X be the set of nodes definied in the proof of Theorem 5.1, let Y be the set defined above, and assume that c is strictly positive. The minimal cut (X, X) is unique if and only if (X, X) = (Y, Y).
We must show that if (X, X) = (Y, Y) and if (Z, Z) is any minimal cut, then (X, X) = (Z, Z).
First note that if (X, X) = (Y, Y), then both equal (X, Y). For, X ⊆ Y by Theorem 5.5 hence (X, Y) ⊆ (Y, Y). On the other hand, if (u, v) ∈ (X, X) = (Y, Y), then u ∈ X and v ∈ Y so (u, v) ∈ (X, Y).
For the arbitrary minimal cut (Z, Z), we have, again by Theorem 5.5 and its analogue for (Y, Y), that X ⊆ Z, Y ⊆ Z . Thus (X, Y) ⊆ (Z, Y) ⊆ (Z, Z). Hence c(X, Y) ≤ c(Z, Z). Now if (X, Y) ⊂ (Z, Z) then eather some arcs of (Z, Z) have zero capacity, contradicting our assumtion c > 0, or c(X, Y) < c(Z, Z), contradicting the minimality of (Z, Z). Thus (X, X) = (Y, Y) = (Z, Z).
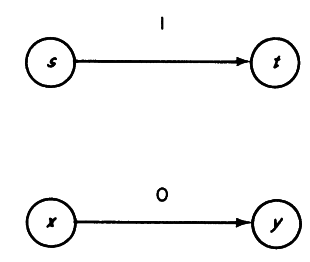
Notice that Theorem 5.6 is not valid if the assumption c > 0 is relaxed to c ≥ 0. For instance in the network shown in 4↓, X = {s}, Y = {t},
and (X, X) = (Y, Y) = (s, t). However, (Z, Z) with Z = {s, x} is another minimal cut that contains both arcs.
References
[1] G. B. Dantzig, "Application of the Simplex Method to a Transportation Problem," Activity Analysis of Production and Allocation, Cowles Commission Monograph 13, Wiley, 1951, 359-373