\sloppy
1 Degraded broadcast channel
X → Y1 → Y2
R2 < I(U;Y2)
R1 < I(X;Y1|U)
for some joint distribution
p(u)p(u|x)p(y1y2|x) |U| ≤ min{|X1|, |X2|, |Y|}
Receiver 2:
Ei = Pr((U(i), Y2)) ∈ A(n)ϵ
Pe(2) = P(Ec1) + ⎲⎳i ≠ 1P(Ei) ≤ ϵ + 2nR22 − n(I(U, Y2) − 2ϵ) ≤ 2ϵ
R2 ≤ I(U;Y2) n → ∞ Pe(2) → ∞
Receiver 1:
Eĩ = Pr(U(i), Y1) ∈ A(n)ϵ
Eij̃ = Pr(U(i), X(i, j), Y1) ∈ A(n)ϵ
Pe = P(Ec1) + P(Ec11) + ⎲⎳i ≠ 1P(Ei) + ⎲⎳j ≠ 1P(E1j)
2 Capacity theorem recall
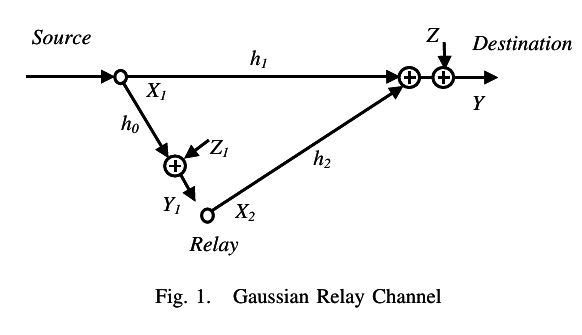
General relay channel
C = maxp(x1x2)I(X1X2;Y), I(X1;Y, Y1|X2)
Degraded relay channel
C = maxp(x1x2)I(X1X2;Y), I(X1;Y1|X2)
y = y1 + x2 + z2 z2 ~ N(0, N2)
How should x2 use the knowledge of x1 (obtained through y1) to help y to understand x1?
We shall show that the capacity is
C* = max0 ≤ α ≤ 1min⎧⎩C⎛⎝(P1 + P2 + √(αP1P2))/(N1 + N2)⎞⎠, C⎛⎝(αP)/(N1)⎞⎠⎫⎭
Channel (X1xX2xY1xY) is degraded if
p(x1, x2, y, y1) = p(x1)p(x2)p(y1|x1)p(y|x1x2) =
p(y, y1|x1x2) = p(y|x1x2) = p(y1|x1x2)p(y|y1x2)
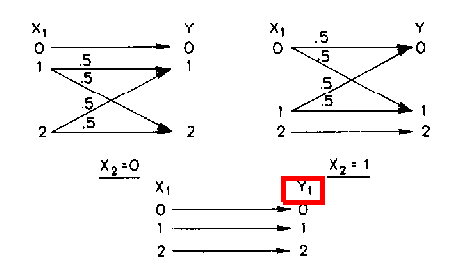
3 Capacity Theorem Example (revisited)
The channel as shown in has X\mathnormal1 = Y = Y\mathnormal1 = \mathnormal\mathnormal\mathnormal{0, 1, 2}, X\mathnormal2 = \mathnormal{0, 1}, and the conditional probability p(y, y1|x1, x2) statisfies ↓. Specifically, the channel operation is:
(1) y1 ≡ x1
and
p(y|y1, x2 = 0) =
y1 = 0
y1 = 1
y1 = 2
\overset
y = 0
y = 1
y = 2
⎡⎢⎢⎢⎣
1
0
0
0
0.5
0.5
0
0.5
0.5
⎤⎥⎥⎥⎦
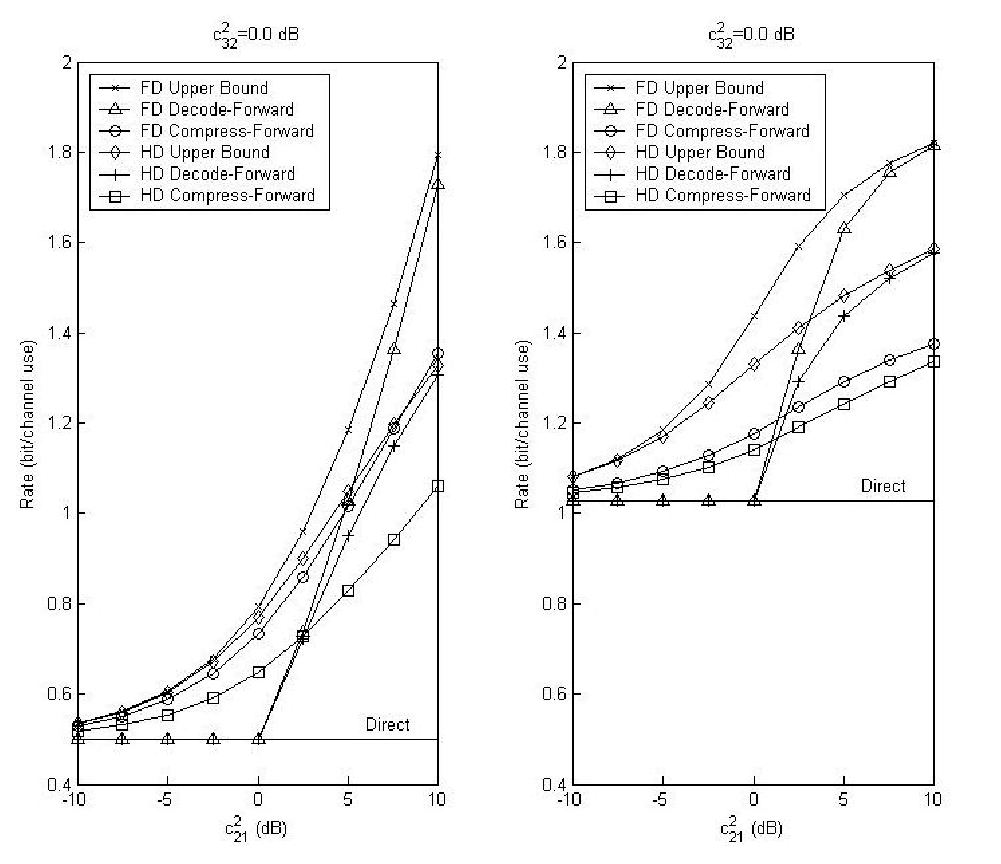
Sato calculated a cooperative upper bound to the channel capacity of the channel, RUG = maxp(x1, x2)I(X1, X2;Y) = 1.170.
By restricting the relay encoding functions to
i)
x2i = f(y11, ..., y1i − 1) = f(y1i − 1)
1 < i ≤ n,
ii)
x2i = f(y11, ..., y1i − 1) = f((y1i − 2, y1i − 1)
1 < i ≤ n.
Sato calculated two lower bounds to the capacity of the channel:
i)
R1 = 1.0437
ii)
R2 = 1.0549
p(y|x1x2) p(x1x2, y)
y|x1x2
y0
y1
y2
00
1
0
0
10
0
0.5
0.5
20
0
0.5
0.5
01
0.5
0.5
0
11
0.5
0.5
0
21
0
0
1
y|x1x2
y0
y1
y2
p(x1x2)
00
p
0
0
p
10
0
0.5p
0.5p
p
20
0
0.5p
0.5p
p
01
0.5p
0.5p
0
p
11
0.5p
0.5p
0
p
21
0
0
p
p
p(y)
2p
2p
2p
I(X1X2;Y) = H(X1X2) − H(Y|X1X2) = − 6⋅plog(p) − H(Y|X1X2)
H(Y|X1X2) = − p⎛⎝2plogp + 2⋅(p)/(2)⋅log⎛⎝(p)/(2)⎞⎠ + 2⋅(p)/(2)⋅log⎛⎝(p)/(2)⎞⎠ + 2⋅(p)/(2)⋅log⎛⎝(p)/(2)⎞⎠ + 2⋅(p)/(2)⋅log⎛⎝(p)/(2)⎞⎠⎞⎠ =
= − p⎛⎝(p)/(2)logp + p⋅log⎛⎝(p)/(2)⎞⎠ + p⋅log⎛⎝(p)/(2)⎞⎠ + p⋅log⎛⎝(p)/(2)⎞⎠ + p⋅log⎛⎝(p)/(2)⎞⎠⎞⎠ = − p⎛⎝(p)/(2)logp + 4p⋅log⎛⎝(p)/(2)⎞⎠⎞⎠ = − p2⎛⎝2logp + 4⋅log⎛⎝(p)/(2)⎞⎠⎞⎠ =
= − p2(2logp + 4⋅log(p) − 4) = − p2(6logp − 4)
I(X1X2;Y) = − 6⋅plog(p) + p2(6logp − 4) = 6⋅plog(p) + 6p2logp − 4p2
(d)/(dp)(I(X1X2;Y)) = 0 → p = 0.1851962117; → maxpI(X1X2;Y) = 1.389606737
R − ϵ ≤ (1)/(n)⋅logM → M ≥ 2n(R − ϵ)
——————————————————————————–————————————
Gaussian degraded relay channel.
X1 = √(α⋅(P1)/(P2))X2 + X10
x1(w|s) = x1̃(w) + √((αP1)/(P2))x2(s)
EX21 = αP1 + αP1 = P1
Јас би го разбрал ова како снага од X1 што оди кон релето (1 − α) и снага што оди кон приемникот α.
X2 ~ N(0, P2), X10 ~ N(0, αP1)
y1i = x1i + z1i
yi = x2i + y1i + zi = x2i + x1i + z1i + zi
R0 ≤ I(X2;Y)
R ≤ I(X1;Y|X2) + R0 = I(X1;Y|X2) + I(X2;Y) = I(X1X2;Y)
I(X2;Y) = H(Y) − H(Y|X2) = H(X2 + X1 + Z1 + Z) − H(X2 + X1 + Z1 + Z|X1) = (1)/(2)log2πe(P2 + P1 + N1 + N2) − (1)/(2)⋅log2πe(P2 + N1 + N2)
(1)/(2)log2πe(P2 + P1 + N1 + N2) − (1)/(2)⋅log2πe(P2 + N1 + N2) = (1)/(2)log⎛⎝(P1)/(P2 + N1 + N2) + 1⎞⎠
x1|y1
X2 = √((P2)/(αP1))(X1 + X10)
I(X2;Y) = H(Y) − H(Y|X2) = H(X2 + Z1) − H(X2 + Z1|X2) = (1)/(2)log2πe(E(X22) + N1) − (1)/(2)⋅log2πe(N1) = (1)/(2)log((E(X22) + N1))/(N1) = C⎛⎝(P2)/(N1)⎞⎠
E(X22) = (P2)/(αP1)(P1 − αP1) = (P2)/((1 − α)) + (αP2)/(α) = (P2 − αP2)/((1 − α)) = P2
x1(w|s) = x1̃(w) + √((αP1)/(P2))x2(s)
C* = supP{min{I(X1;Y, Ŷ1|X2U) + I(U;Y1|X2, V), I(X1, X2;Y) − I(Ŷ1, Y1|X1X2U, V)}}
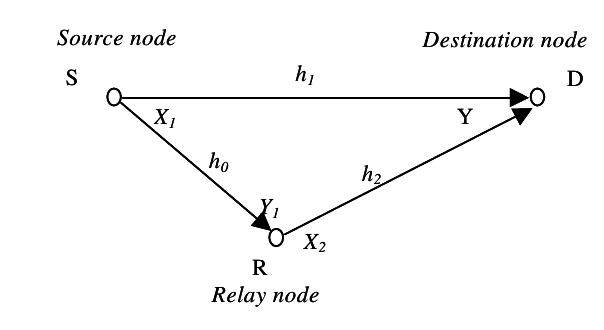
4 Khojastepour, Lower bounds on capacity of Gaussian relay channel
y = h1x1 + h2x2 + z y1 = h0x1 + z1 z ~ N(0, N) z1 ~ N(0, N1)
E[X21] ≤ P1 E[X22] ≤ P2
xn1:M → Rn x2i = fi(Y11Y12, ..., Y1(i − 1)) for 1 ≤ i ≤ n
C ≥ C⎛⎝S31 + (S21S31)/(S31 + S21 + S32 + 1)⎞⎠
RUT = (1)/(4)log(P1)/(D1)
D1 = (P1N)/(N + h21P1 + (⟨α̃, β⟩)/(1 + ||β||2)P1) α = h0 β = h2⋅√((P2)/(h20P1 + N1)) γ0 = (|h0|2)/(N1) γ1 = (|h1|2)/(N) γ2 = (|h2|2)/(N)
D1 = (P1N⋅⎛⎝1 + (h22P2)/(h20P1 + N1)⎞⎠)/((N + h21P1)⎛⎝1 + (h22P2)/(h20P1 + N1)⎞⎠ + P1⋅h0⋅h2⋅√((P2)/(h20P1 + N1))) = (P1N⋅⎛⎝(h20P1 + N1 + h22P2)/(h20P1 + N1)⎞⎠)/((N + h21P1)⎛⎝(h20P1 + N1 + h22P2)/(h20P1 + N1)⎞⎠ + h0h2⋅√((P2)/(h20P1 + N1))) = (P1N⋅(h20P1 + N1 + h22P2))/((N + h21P1)(h20P1 + N1 + h22P2) + (h20P1 + N1)⋅h0h2⋅√((P2)/(h20P1 + N1))) =
(P1N⋅(h20P1 + N1 + h22P2))/((N + h21P1)(h20P1 + N1 + h22P2) + √((h20P1 + N1))⋅h0h2⋅√(P2)) = (P1N⋅N1⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1⎛⎝1 + (h21)/(N)P1⎞⎠⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√(⎛⎝(h20)/(N1)P1 + 1⎞⎠)⋅h0h2⋅√(P2)) = (P1N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))
(P1)/(D1) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) + (√(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = 1 + γ1P1 + (√((γ0P1 + 1))⋅h0⋅√(h22P2))/(N⋅√(N1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) =
= 1 + γ1P1 + (√((γ0P1 + 1))⋅h0⋅√((h22)/(N1)P2))/(N⋅⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = 1 + γ1P1 + (√(γ0P1 + 1)⋅h0⋅√(γ2P2))/(N⋅(γ0P1 + 1 + γ2P2))
(P1N⋅(h20P1 + N1 + h22P2))/((N + h21P1)(h20P1 + N1 + h22P2) + √((h20P1 + N1))⋅h0h2⋅√(P2)) = (P1N⋅N1⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1⎛⎝1 + (h21)/(N)P1⎞⎠⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√(⎛⎝(h20)/(N1)P1 + 1⎞⎠)⋅h0h2⋅√(P2)) = (P1N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))
(P1)/(D1) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + √(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) + (√(N1)√((γ0P1 + 1))⋅h0h2⋅√(P2))/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = 1 + γ1P1 + (√((γ0P1 + 1))⋅h0⋅√(h22P2))/(N⋅√(N1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) =
= 1 + γ1P1 + (√((γ0P1 + 1))⋅h0⋅√((h22)/(N1)P2))/(N⋅⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = 1 + γ1P1 + (√(γ0P1 + 1)⋅h0⋅√(γ2P2))/(N⋅(γ0P1 + 1 + γ2P2))
D1 = (P1N⋅⎛⎝1 + (h22P2)/(h20P1 + N1)⎞⎠)/((N + h21P1)⎛⎝1 + (h22P2)/(h20P1 + N1)⎞⎠ + P1⋅h0) = (P1N⋅⎛⎝(h20P1 + N1 + h22P2)/(h20P1 + N1)⎞⎠)/((N + h21P1)⎛⎝(h20P1 + N1 + h22P2)/(h20P1 + N1)⎞⎠ + P1h0) = (P1N⋅(h20P1 + N1 + h22P2))/((N + h21P1)(h20P1 + N1 + h22P2) + (h20P1 + N1)⋅h0⋅P1) =
(P1N⋅(h20P1 + N1 + h22P2))/((N + h21P1)(h20P1 + N1 + h22P2) + (h20P1 + N1)⋅h0P1) = (P1N⋅N1⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1⎛⎝1 + (h21)/(N)P1⎞⎠⎛⎝(h20)/(N1)P1 + 1 + (h22)/(N1)P2⎞⎠ + (h20P1 + N1)⋅h0P1) = (P1N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + (h20P1 + N1)⋅h0P1)
(P1)/(D1) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠ + (h20P1 + N1)⋅h0P1)/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = (NN1(1 + γ1P1)⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠)/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) + ((h20P1 + N1)⋅h0P1)/(N⋅N1⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) = 1 + γ1P1 + (⎛⎝(h20)/(N1)P1 + 1⎞⎠⋅(h0)/(N)P1)/(⎛⎝γ0P1 + 1 + (h22)/(N1)P2⎞⎠) =
= 1 + γ1P1 + ((γ0P1 + 1)⋅(h0)/(N)P1)/((γ0P1 + 1 + γ2P2))
- Без директна компонента:
z ~ N(0, N) z1 ~ N(0, N1)
y1 = h0x1 + z1 y2 = h2x2 + z γ0 = (|h0|2)/(N1) γ1 = (|h1|2)/(N) γ2 = (|h2|2)/(N)
ŷ1 = √((P2)/(h20P1 + N1))y1 = h0√((P2)/(h20P1 + N1))x1 + √((P2)/(h20P1 + N1))z1 y2 = h2ŷ1 + z = h2⋅h0⋅√((P2)/(h20P1 + N1))x1 + h2⋅√((P2)/(h20P1 + N1))z1 + z
D = I(X1;Y2) = h(Y2) − h(Y2|X1) = h(h2⋅h0⋅√((P2)/(h20P1 + N1))x1 + h2⋅√((P2)/(h20P1 + N1))z1 + z) − h(Z1 + Z) =
= (1)/(2)log2πe⎛⎝h22⋅h20⋅(P2)/(h20P1 + N1)P1 + (h22⋅P2)/(h20P1 + N1)⋅N1 + N⎞⎠ − (1)/(2)log2πe⋅⎛⎝(h22⋅P2N1)/(h20P1 + N1) + N⎞⎠
= (1)/(2)log(h22⋅(h20)/(N1)⋅(P2)/(γ0P1 + 1)⋅P1 + \mathchoice(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N)/(⎛⎝N1⋅(h22P2)/(h20P1 + N1) + N⎞⎠) = (1)/(2)log⎛⎜⎜⎜⎝1 + ((h22⋅P2⋅γ0⋅P1)/(γ0P1 + 1))/(N⋅⎛⎜⎝((h22)/(N)P2)/(γ0P1 + 1) + 1⎞⎟⎠)⎞⎟⎟⎟⎠ = \mathchoice(1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠
со директна компонента
y = h1x1 + h2x2 + z y1 = h0x1 + z1 z ~ N(0, N) z1 ~ N(0, N1)
x2 = √((P2)/(h20P1 + N1))y1 = h0√((P2)/(h20P1 + N1))x1 + √((P2)/(h20P1 + N1))z1 y = h1x1 + h2x2 + z = h1x1 + h2⋅h0⋅√((P2)/(h20P1 + N1))x2 + h2⋅√((P2)/(h20P1 + N1))z1 + z =
I(X1;Y) = h(Y) − h(Y|X1) = h(Y) − h(h1X1 + h2√((P2)/(h20P1 + N1))X1 + h2√((P2)/(h20P1 + N1))z1 + z|X1) =
D = I(X1;Y2) = h(Y2) − h(Y2|X1) = h(h1X1 + h2⋅h0⋅√((P2)/(h20P1 + N1))x1 + h2⋅√((P2)/(h20P1 + N1))z1 + z) − h(h2√((P2)/(h20P1 + N1))z1 + z) =
= (1)/(2)log2πe⎛⎝h21P1 + h22⋅h20⋅(P2)/(h20P1 + N1)P1 + (h22⋅P2)/(h20P1 + N1)⋅N1 + N⎞⎠ − (1)/(2)log2πe⋅⎛⎝(h22⋅P2N1)/(h20P1 + N1) + N⎞⎠ =
= (1)/(2)log(h21P1 + h22⋅(h20)/(N1)⋅(P2)/(γ0P1 + 1)⋅P1 + \mathchoice(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N(h22⋅P2)/(h20P1 + N1)⋅N1 + N)/(⎛⎝N1⋅(h22P2)/(h20P1 + N1) + N⎞⎠) = (1)/(2)log⎛⎜⎜⎜⎝1 + (h21P1 + (h22⋅P2⋅γ0⋅P1)/(γ0P1 + 1))/(N⋅⎛⎜⎝((h22)/(N)P2)/(γ0P1 + 1) + 1⎞⎟⎠)⎞⎟⎟⎟⎠
(1)/(2)log⎛⎜⎜⎝1 + (γ1P1 + (γ2⋅P2⋅γ0⋅P1)/(γ0P1 + 1))/(⎛⎝(γ2P2)/(γ0P1 + 1) + 1⎞⎠)⎞⎟⎟⎠ = \mathchoice(1)/(2)log⎛⎝1 + (γ1P1(γ0P1 + 1) + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ1P1(γ0P1 + 1) + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ1P1(γ0P1 + 1) + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠(1)/(2)log⎛⎝1 + (γ1P1(γ0P1 + 1) + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠ = (1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠
(γ1P1(γ0P1 + 1) + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1) = (γ1P1γ0P1 + γ1P1 + γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1) = (γ1P1γ0P1 + γ2⋅P2⋅γ0⋅P1 + γ1P1)/(γ2P2 + γ0P1 + 1) = ((γ1P1 + γ2⋅P2⋅)γ0⋅P1 + γ1P1)/(γ2P2 + γ0P1 + 1)
5 Ризински, Кафеџиски, Capacity Bounds and Achievable Rates
6 Khojastepour, Distributed cooperative communications in wireless networks (PhD Thesis)
Y1 = h0X1 + Z1 Y = h1X1 + Z
Ова е наубавиот досега доказ за пресметка на горна граница на условна ентропија во Гаусов релеен канал!!!! Секогаш оди на овој начин!!!
(2) h(Y1|Y)\overset(a) = Ey[h(Y1|y)]\overset(b) ≤ Ey⎡⎣(1)/(2)log(2πe)Var(Y1|y)⎤⎦\overset(c) ≤ (1)/(2)log(2πe)Ey[Var(Y1|y)]\overset(d) ≤ (1)/(2)log(2πe)⎡⎣E[Y21] − (E2[Y, Y1])/(E[Y2])⎤⎦ = (△)
(a) - Deffiniton of conditional entropy
(b) - Gaussian maximizes entropy
(c) - Jensen’s inequality
(d) - Swarthz Inequality
[Y21] − (E2[Y, Y1])/(E[Y2]) = h20E[X21] + N1 − (E2[Y, Y1])/(h21E[X21] + N) = (*)
E2[Y, Y1] = E2[(h0X1 + N1)(h1X1 + N)] = E2[h0h1X21 + h0X1N + h1X1N1 + N1N] = h20h21E2[X21]
(*) = ((h20E[X21] + N1)(h21E[X21] + N) − h20h21E2[X21])/(h21E[X21] + N) = (\cancelh20h21E2[X21] + N⋅h20E[X21] + N1h21E[X21] + N1N − \cancelh20h21E2[X21])/(h21E[X21] + N) = ((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)
(△) = (1)/(2)log(2πe)((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)
- Сега ќе го поминам Bound on I(X1i;Yi, Y1i|m1) (демек вектроска варијанта, зошто ова горе беше упростена скаларна варијанта)
∑ki = 1I(X1i;Yi, Y1i|m1) ≤ ∑ki = 1[h(Yi) + h(Y1i|Yi) − h(YiY1i|m1X1i)] = ∑ki = 1[h(Yi) + h(Y1i|Yi) − h(Yi|X1i) − h(Y1i|X1iYi)] =
\overset(e) = ∑ki = 1⎡⎣h(Yi) + \mathchoiceh(Y1i|Yi)h(Y1i|Yi)h(Y1i|Yi)h(Y1i|Yi) − (1)/(2)log(2πe)N − (1)/(2)log(2πe)N1⎤⎦
(e) - Гледај го h(Y1i|X1iYi). Кога го знаеш X1, Yi не содржи дополнителна корисна информација за Y1 која веќе X1 не ја содржи.
\mathchoiceh(Y1i|Yi)h(Y1i|Yi)h(Y1i|Yi)h(Y1i|Yi) = Ey[h(Y1i|yi)] ≤ Ey⎡⎣(1)/(2)log(2πe)Var(Y1i|yi)⎤⎦\overset ≤ (1)/(2)log(2πe)Ey[Var(Y1i|yi)]\overset ≤ (1)/(2)log(2πe)\mathchoice⎡⎣E[Y1i] − (E2[Yi, Y1i])/(E[Y2i])⎤⎦⎡⎣E[Y1i] − (E2[Yi, Y1i])/(E[Y2i])⎤⎦⎡⎣E[Y1i] − (E2[Yi, Y1i])/(E[Y2i])⎤⎦⎡⎣E[Y1i] − (E2[Yi, Y1i])/(E[Y2i])⎤⎦ = (\triangledown)
[Y1i] − (E2[Yi, Y1i])/(E[Y2]) = h20E[X21] + N1 − (E2[Yi, Y1i])/(h21E[X21] + N) = (*)
E2[Yi, Y1i] = E2[(h0X1 + Z1)(h1X1 + Z)] = E2[h0h1X21 + h0X1Z + h1X1Z1 + Z1Z] = h20h21E2[X21]
(*) = ((h20E[X21] + N1)(h21E[X21] + N) − h20h21E2[X21])/(h21E[X21] + N) = (\cancelh20h21E2[X21] + N⋅h20E[X21] + N1h21E[X21] + N1N − \cancelh20h21E2[X21])/(h21E[X21] + N) = \mathchoice((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)
(\triangledown) = (1)/(2)log(2πe)((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N)
h(Yi) ≤ (1)/(2)log2πe(Var(Yi)) = (1)/(2)log2πe(h21E[X21i] + N)
∑ki = 1I(X1i;Yi, Y1i|m1) = ∑ki = 1(1)/(2)log2πe(h21E[X21i] + N) + (1)/(2)log2πe⋅((N⋅h20 + N1h21)E[X21] + N1N)/(h21E[X21] + N) − (1)/(2)log(2πe)N⋅N1 =
= ∑ki = 1(1)/(2)log2πe\cancel(h21E[X21i] + N)⋅((N⋅h20 + N1h21)E[X21] + N1N)/(\cancelh21E[X21] + N) − (1)/(2)log(2πe)N⋅N1 = ∑ki = 1(1)/(2)log((N⋅h20 + N1h21)E[X21] + N1N)/(N⋅N1) =
= ∑ki = 1(1)/(2)log⎛⎝⎛⎝(N⋅h20)/(N⋅N1) + (N1h21)/(N⋅N1)⎞⎠E[X21] + 1⎞⎠ = k⋅(1)/(k)⋅(1)/(2)⋅∑ki = 1log⎛⎝1 + ⎛⎝(h20)/(N1) + (h21)/(N)⎞⎠E[X21]⎞⎠ ≤ (k)/(2)⋅log⎛⎝1 + ⎛⎝(h20)/(N1) + (h21)/(N)⎞⎠⋅\underset ≤ P0(1)/(k)⋅∑ki = 1E[X21]⎞⎠
∑ki = 1I(X1i;Yi, Y1i|m1) = (k)/(2)⋅log⎛⎝1 + (h20P0)/(N1) + (h21P0)/(N)⎞⎠
7 S. Zahedi, M.Mohseni, On the capacity of AWGN relay channels with linеar relaying functions.
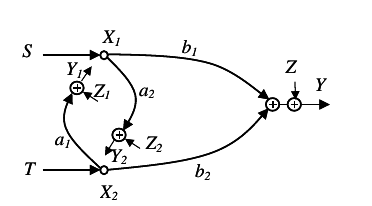
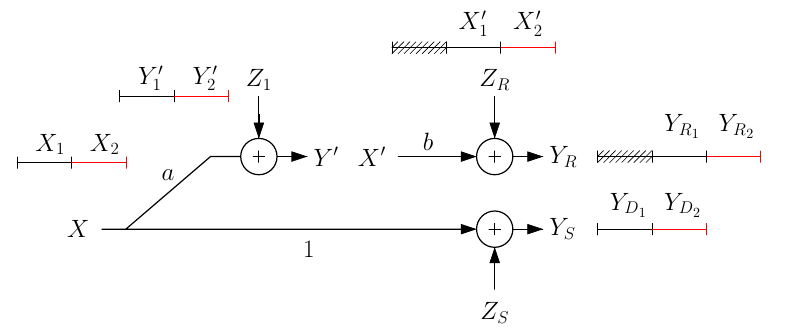
7.1 Linear Relaying Example for Generал AWGN Relay Channel
\mathchoiceX1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
H(Y2|Y1) = (1)/(2)log⎛⎝E(Y22) − (E2(Y1Y2))/(E(Y21))⎞⎠ = (1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(E(X21) + N)⎞⎠ =
Expand[((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − b2⋅d2⋅N2] = − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP
H(Y1, Y2) = (1)/(2)log2πe(2αP + N) + (1)/(2)log2πe⎛⎝( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)/(2αP + N)⎞⎠ =
= (1)/(2)log(2πe)2( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)
H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) =
= (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2] = 2a2αb2d2NP + 2a2αNP + N2
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) = (1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) =
= (1)/(2)log( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(N⋅(2a2αb2d2NP + 2a2αNP + N2))
1 + N2⎛⎝ − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N)⎞⎠⋅(2⋅a2⋅(αP)/(N) + 1)/(N2⎛⎝2a2αb2d2(P)/(N) + 2a2α(P)/(N) + 1⎞⎠) =
= 1 + \undersetA⎛⎝ − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N)⎞⎠⋅(1)/(⎛⎜⎜⎝(2a2αb2d2(P)/(N))/(2⋅a2⋅(αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/(⎛⎜⎜⎝(a2b2d2⋅(2αP)/(N))/(a2⋅(2αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/(⎛⎜⎜⎝(a2b2d2⋅(2αP)/(N))/(a2⋅(2αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/((a2b2d4 + 1))
d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
A = − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N) = ⎛⎝ − 2⋅a2α2(P)/(N) + a2αb2d2 + 2a2α(P)/(N) − α + 1⎞⎠⋅2⋅(P)/(N) = ⎛⎝2a2α(P)/(N) − 2⋅a2α2(P)/(N) + a2αb2d2 − α + 1⎞⎠⋅2⋅(P)/(N) =
⎛⎝2a2α(P)/(N)⋅(1 − α) + a2αb2d2 − α + 1⎞⎠⋅2⋅(P)/(N) = ⎛⎝2a2α(P)/(N)⋅(1 − α) + (1 − α) + a2αb2d2⎞⎠⋅2⋅(P)/(N) = ⎛⎝⎛⎝a2(2αP)/(N) + 1⎞⎠⋅(1 − α) + a2αb2d2⎞⎠⋅2⋅(P)/(N)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = X2’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
H(Y2|Y1) = (1)/(2)log⎛⎝E(Y22) − (E2(Y1Y2))/(E(Y21))⎞⎠ = (1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(E(X21) + N)⎞⎠ =
= (1)/(2)log⎛⎝(1 − α)/(α)⋅2αP + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N − (b2⋅d2⋅a4⋅E2((X21)) + b2⋅d2⋅N2)/(2⋅a2⋅αP + N)⎞⎠ =
= (1)/(2)log⎛⎝(((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − b2⋅d2⋅N2)/(2αP + N)⎞⎠
Expand[((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − b2⋅d2⋅N2] = − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP
H(Y2|Y1) = (1)/(2)log⎛⎝( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)/(2αP + N)⎞⎠ =
H(Y1, Y2) = (1)/(2)log2πe(2αP + N) + (1)/(2)log2πe⎛⎝( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)/(2αP + N)⎞⎠ =
= (1)/(2)log(2πe)2( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)
H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) =
= (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2] = 2a2αb2d2NP + 2a2αNP + N2
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) = (1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) =
= (1)/(2)log( − 4a2α2P2 + 4a2αb2d2NP + 2a2αNP + 4a2αP2 − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(N⋅(2a2αb2d2NP + 2a2αNP + N2))
( − 4a2α2P2 + \cancelto24a2αb2d2NP + \cancel2a2αNP + 4a2αP2 − 2αNP + \cancelN2 + 2NP)⋅(2⋅a2⋅(αP)/(N) + 1)/((2a2αb2d2NP + 2a2αNP + N2)) =
= 1 + ( − 4a2α2P2 + 2a2αb2d2NP + 4a2αP2 − 2αNP + 2NP)⋅(2⋅a2⋅(αP)/(N) + 1)/((2a2αb2d2NP + 2a2αNP + N2)) =
1 + N2⎛⎝ − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N)⎞⎠⋅(2⋅a2⋅(αP)/(N) + 1)/(N2⎛⎝2a2αb2d2(P)/(N) + 2a2α(P)/(N) + 1⎞⎠) =
= 1 + \undersetA⎛⎝ − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N)⎞⎠⋅(1)/(⎛⎜⎜⎝(2a2αb2d2(P)/(N))/(2⋅a2⋅(αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/(⎛⎜⎜⎝(a2b2d2⋅(2αP)/(N))/(a2⋅(2αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/(⎛⎜⎜⎝(a2b2d2⋅(2αP)/(N))/(a2⋅(2αP)/(N) + 1) + 1⎞⎟⎟⎠) = 1 + A⋅(1)/((a2b2d4 + 1))
d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
A = − 4a2α2(P2)/(N2) + 2a2αb2d2(P)/(N) + 4a2α(P2)/(N2) − 2α(P)/(N) + 2(P)/(N) = ⎛⎝ − 2⋅a2α2(P)/(N) + a2αb2d2 + 2a2α(P)/(N) − α + 1⎞⎠⋅2⋅(P)/(N) = ⎛⎝2a2α(P)/(N) − 2⋅a2α2(P)/(N) + a2αb2d2 − α + 1⎞⎠⋅2⋅(P)/(N) =
⎛⎝2a2α(P)/(N)⋅(1 − α) + a2αb2d2 − α + 1⎞⎠⋅2⋅(P)/(N) = ⎛⎝2a2α(P)/(N)⋅(1 − α) + (1 − α) + a2αb2d2⎞⎠⋅2⋅(P)/(N) = ⎛⎝⎛⎝a2(2αP)/(N) + 1⎞⎠⋅(1 − α) + a2αb2d2⎞⎠⋅2⋅(P)/(N)
(√((1 − α)/(α)) + abd)2 = (1 − α)/(α) + 2abd((1 − α))/(α) + a2b2d2
⎛⎝⎛⎝a2(2αP)/(N) + 1⎞⎠⋅((1 − α))/(α) + a2b2d2⎞⎠⋅(2⋅αP)/(N) = ⎛⎝a2(2αP)/(N)⋅((1 − α))/(α) + ((1 − α))/(α) + a2b2d2⎞⎠⋅2⋅(αP)/(N)
\mathchoiceX1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(a2⋅2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
Expand⎡⎣((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2⎤⎦ = 4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP
\mathchoiceH(Y1, Y2)H(Y1, Y2)H(Y1, Y2)H(Y1, Y2) = (1)/(2)log2πe(a22αP + N) + (1)/(2)log2πe⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ = \mathchoice(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)
Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
\mathchoiceH(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1⋅(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅α⋅P⋅N + N2] = 2a2αb2d2NP + 2a2αNP + N2
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) = \mathchoice(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) =
= (1)/(2)log(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(N⋅(2a2αb2d2NP + 2a2αNP + N2))
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(a2⋅2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
H(Y2|Y1) = (1)/(2)log⎛⎝E(Y22) − (E2(Y1Y2))/(E(Y21))⎞⎠ = (1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(a2⋅E(X21) + N)⎞⎠ =
(1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(√((1 − α)/(α))X1 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(a2⋅E(X21) + N)⎞⎠
= (1)/(2)log(2πe)⎛⎜⎝(1 − α)/(α)⋅2αP + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N − (b2⋅d2⋅a4⋅E2((X21)) + a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 + b2⋅d2⋅N2)/(2⋅a2⋅αP + N)⎞⎟⎠ =
= (1)/(2)log(2πe)⎛⎜⎝(((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)⋅(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2)/(a2⋅2αP + N)⎞⎟⎠
Expand⎡⎣((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2⎤⎦ = 4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP
H(Y2|Y1) = (1)/(2)log(2πe)⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ =
\mathchoiceH(Y1, Y2)H(Y1, Y2)H(Y1, Y2)H(Y1, Y2) = (1)/(2)log2πe(a22αP + N) + (1)/(2)log2πe⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ = \mathchoice(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)
Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
\mathchoiceH(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1⋅(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) + N = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅αP⋅N + N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2 + 2⋅a2⋅α⋅P⋅N + N2] = 2a2αb2d2NP + 2a2αNP + N2
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) = \mathchoice(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP + 2a2αNP + N2)/(2⋅a2⋅αP + N) =
= (1)/(2)log(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(N⋅(2a2αb2d2NP + 2a2αNP + N2))
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
R = max0 ≤ α ≤ 1(1)/(2)C⎛⎝(2αP)/(N)⎛⎝1 + ((√((1 − α)/(α)) + abd)2)/(1 + b2d2)⎞⎠⎞⎠
(√((1 − α)/(α)) + abd)2 = (1 − α)/(α) + 2abd((1 − α))/(α) + a2b2d2
(√((1 − α)/(α)) + abd)2 = (1 − α)/(α) + 2abd((1 − α))/(α) + a2b2d2
(\cancelto24a2αb2d2NP + \cancel2a2αNP − 2αNP + \cancelN2 + 2NP)⋅(2⋅a2⋅(αP)/(N) + 1)/((2a2αb2d2NP + 2a2αNP + N2)) = ⎛⎝(2a2αb2d2NP − 2αNP + 2NP)/((2a2αb2d2NP + 2a2αNP + N2)) + 1⎞⎠⋅⎛⎝2⋅a2⋅(αP)/(N) + 1⎞⎠ =
= 2⋅a2⋅(αP)/(N) + 1 + (2a2αb2d2NP − 2αNP + 2NP)⋅(2⋅a2⋅(αP)/(N) + 1)/((2a2αb2d2NP + 2a2αNP + N2)) =
I(X1X2;Y1Y2) = C⎛⎜⎝(2Pα)/(N)⎛⎜⎝a2 + (⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1))⎞⎟⎠⎞⎟⎠
⎛⎜⎝a2 + (⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1))⎞⎟⎠ = ⎛⎜⎝((a2b2d4 + 1)⋅a2 + a2b2d2 + (1 − α)/(α))/((a2b2d4 + 1))⎞⎟⎠ = ⎛⎜⎝(a4b2d4 + a2 + a2b2d2 + (1 − α)/(α))/((a2b2d4 + 1))⎞⎟⎠
= 2⋅a2⋅(αP)/(N) + 1 + (2a2αb2d2NP − 2αNP + 2NP)⋅(2⋅a2⋅(αP)/(N) + 1)/((2a2αb2d2NP + 2a2αNP + N2)) =
= 2⋅a2⋅(αP)/(N) + 1 + (2a2αb2d2NP − 2αNP + 2NP)⋅(a2⋅(2αP)/(N) + 1)/(N2⎛⎝a2b2d2(2αP)/(N) + a2(2αP)/(N) + 1⎞⎠) = 2⋅a2⋅(αP)/(N) + 1 + 2NP(a2αb2d2 − α + 1)⋅(1)/(N2⎛⎜⎜⎝a2b2d2((2αP)/(N))/(2⋅a2⋅(αP)/(N) + 1) + 1⎞⎟⎟⎠) =
= 1 + 2⋅a2⋅(αP)/(N) + 2P(a2αb2d2 − α + 1)⋅(1)/(N(a2b2d4 + 1)) = 1 + a2⋅(2αP)/(N) + (2Pα)/(N)⋅(⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1)) = 1 + (2αP)/(N)⎛⎜⎝a2 + (⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1))⎞⎟⎠
I(X1X2;Y1Y2) = C⎛⎜⎝(2Pα)/(N)⎛⎜⎝a2 + (⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1))⎞⎟⎠⎞⎟⎠
⎛⎜⎝a2 + (⎛⎝a2b2d2 + (1 − α)/(α)⎞⎠)/((a2b2d4 + 1))⎞⎟⎠ = ⎛⎜⎝((a2b2d4 + 1)⋅a2 + a2b2d2 + (1 − α)/(α))/((a2b2d4 + 1))⎞⎟⎠ = ⎛⎜⎝(a4b2d4 + a2 + a2b2d2 + (1 − α)/(α))/((a2b2d4 + 1))⎞⎟⎠
Проба со испуштање на Z во H(Y1Y2|X1X2):
\mathchoiceX1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(a2⋅2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
Expand⎡⎣((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2⎤⎦ = 4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP
\mathchoiceH(Y1, Y2)H(Y1, Y2)H(Y1, Y2)H(Y1, Y2) = (1)/(2)log2πe(a22αP + N) + (1)/(2)log2πe⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ = \mathchoice(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)
Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
\mathchoiceH(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1⋅(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2] = 2a2αb2d2NP
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N) = \mathchoice(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N) =
= (1)/(2)log(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(2a2αb2d2NP)
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
\mathchoiceX1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)X1 ~ N(0, 2αP) X2 = √((1 − α)/(α))X1 X2’ = d⋅Y1’ Y1 = a⋅X1 + Z1 Z = Z1 = N(0, N)
d -is chosen to satisfy the relay power constraint
R = (1)/(2)I(X1X2;Y1Y2) Дели со два затоа што имаш две употреби на каналот.
I(X1X2;Y1Y2) = H(Y1, Y2) − H(Y1Y2|X1X2) = H(Y1) + H(Y2|Y1) − H(Y1|X1X2) − H(Y2|X1X2Y1) H(Y1) = (1)/(2)log(a2⋅2αP + N)
\mathchoiceY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZY2 = X2 + b⋅X’ + Z X’ = d⋅Y1’ = d⋅a⋅X1 + d⋅Z1 Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
H(Y2|Y1) = (1)/(2)log⎛⎝E(Y22) − (E2(Y1Y2))/(E(Y21))⎞⎠ = (1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(a2⋅E(X21) + N)⎞⎠ =
(1)/(2)log⎛⎝(1 − α)/(α)E[X21] + b2⋅d2⋅a2⋅E[X21] + b2⋅d2⋅N + N − (E2((a⋅X1 + Z1)⋅(√((1 − α)/(α))X1 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z)))/(a2⋅E(X21) + N)⎞⎠
= (1)/(2)log(2πe)⎛⎜⎝(1 − α)/(α)⋅2αP + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N − (b2⋅d2⋅a4⋅E2((X21)) + a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 + b2⋅d2⋅N2)/(2⋅a2⋅αP + N)⎞⎟⎠ =
= (1)/(2)log(2πe)⎛⎜⎝(((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)⋅(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2)/(a2⋅2αP + N)⎞⎟⎠
Expand⎡⎣((1 − α)⋅2⋅P + b2⋅d2⋅a2⋅2αP + b2⋅d2⋅N + N)(2⋅a2⋅αP + N) − b2⋅d2⋅a4⋅4α2P2 − a2⋅⎛⎝(1 − α)/(α)⎞⎠⋅4α2P2 − b2⋅d2⋅N2⎤⎦ = 4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP
H(Y2|Y1) = (1)/(2)log(2πe)⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ =
\mathchoiceH(Y1, Y2)H(Y1, Y2)H(Y1, Y2)H(Y1, Y2) = (1)/(2)log2πe(a22αP + N) + (1)/(2)log2πe⎛⎝(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)/(a2⋅2αP + N)⎞⎠ = \mathchoice(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)(1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)
Y2 = X2 + b⋅d⋅a⋅X1 + b⋅d⋅Z1 + Z
\mathchoiceH(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2)H(Y1Y2|X1X2) = H(Y1|X1X2) + H(Y2|X1X2Y1) = (1)/(2)log2πeN + (1)/(2)log2πe(E[Var(b⋅d⋅Z1 + Z|Y1)]) = (*)
E[Var(b⋅d⋅Z1 + Z|Y1)] = E[Var(b⋅d⋅Z1|Y1)] + N = b2d2E[Z21] − (E2[b⋅d⋅Z1⋅(a⋅X1 + Z1)])/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅E2(Z21))/(2⋅a2⋅αP + N) + N = b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) =
= b2d2N − (b2d2⋅N2)/(2⋅a2⋅αP + N) = (b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2)/(2⋅a2⋅αP + N) = (2a2αb2d2NP)/(2⋅a2⋅αP + N)
Expand[b2d2N(2⋅a2⋅αP + N) − b2d2⋅N2] = 2a2αb2d2NP
(*) = (1)/(2)log2πeN + (1)/(2)log(2πe)⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N) = \mathchoice(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)(1)/(2)log(2πe)2N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N)
I(X1X2;Y1Y2) = (1)/(2)log(2πe)2(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP) − (1)/(2)log(2πe)2⋅N⋅(2a2αb2d2NP)/(2⋅a2⋅αP + N) =
= (1)/(2)log(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + N)/(2a2αb2d2NP)
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)d = √((2αP)/(a22αP + N)) d2 = (2αP)/(a22αP + N) = ((2αP)/(N))/(a2(2αP)/(N) + 1) a2(2αP)/(N) + 1 = (2αP)/(N⋅d2)
R = max0 ≤ α ≤ 1(1)/(2)C⎛⎝(2αP)/(N)⎛⎝1 + ((√((1 − α)/(α)) + abd)2)/(1 + b2d2)⎞⎠⎞⎠
(√((1 − α)/(α)) + abd)2 = (1 − α)/(α) + 2abd((1 − α))/(α) + a2b2d2
(√((1 − α)/(α)) + abd)2 = (1 − α)/(α) + 2abd((1 − α))/(α) + a2b2d2
(4a2αb2d2NP + 2a2αNP − 2αNP + N2 + 2NP)⋅(2⋅a2⋅αP + 1)/(2a2αb2d2N2P) =
Expand[(4⋅a2α⋅b2⋅d2⋅N⋅P + 2a2α⋅N⋅P − 2α⋅N⋅P + N2 + 2⋅N⋅P)⋅(2⋅a2⋅αP + 1)] = 8a4α2b2d2NP2 + 4a4α2NP2 − 4a2α2NP2 + 4a2αb2d2NP + 2a2αN2P + 4a2αNP2 + 2a2αNP − 2αNP + N2 + 2NP
= (8a4α2b2d2NP2 + 4a4α2NP2 − 4a2α2NP2 + 4a2αb2d2NP + 2a2αN2P + 4a2αNP2 + 2a2αNP − 2αNP + N2 + 2NP)/(2a2αb2d2N2P) =
Expand[(4⋅a2α⋅b2⋅d2⋅N⋅P + 2a2α⋅N⋅P − 2α⋅N⋅P + N2 + 2⋅N⋅P)⋅(2⋅a2⋅αP + 1)] = 8a4α2b2d2NP2 + 4a4α2NP2 − 4a2α2NP2 + 4a2αb2d2NP + 2a2αN2P + 4a2αNP2 + 2a2αNP − 2αNP + N2 + 2NP
= (8a4α2b2d2NP2 + 4a4α2NP2 − 4a2α2NP2 + 4a2αb2d2NP + 2a2αN2P + 4a2αNP2 + 2a2αNP − 2αNP + N2 + 2NP)/(2a2αb2d2N2P) =
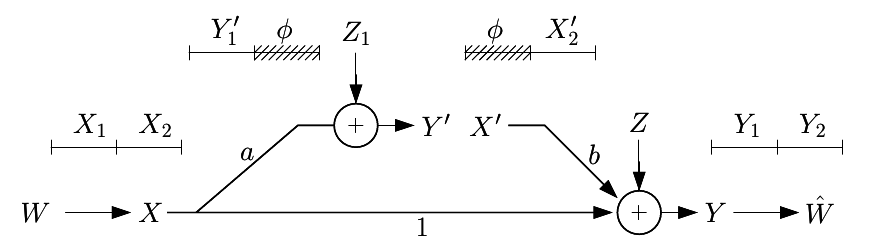
7.2 Linear Relaying Example for FD-AWGN Relay Channel
Неуспешен обид да одам со готовата формула од El Gammal
C ≤ maxp(x1)p(x2)min{I(X1;Y3’) + I(X2;Y3’’), I(X1;Y2, Y3’)}
C ≤ maxp(x1)p(x2)min{I(X1;Ys) + I(X’;YR), I(X1;Y’, Ys)}
I(X1;Ys) = (1)/(2)log(P + N); I(X’;YR) = (1)/(2)log(b2P + N)
C ≤ maxp(x1)p(x2)min{I(X1;Y3’) + I(X2;Y3’’), I(X1;Y2, Y3’)}
C ≤ maxp(x1)p(x2)min{I(X1;Ys) + I(X’;YR), I(X1;Y’, Ys)}
I(X1;Ys) = (1)/(2)log(P + N); I(X’;YR) = (1)/(2)log(b2P + N)
Капацитетот на AF е согласно изразот за Linear Relaying во El Gamal. (Во мојов случај во ~1 тајмслот праќаш X1 а примаш YR1, YD2 и затоа капацитетот се базира врз основ на пресметка на I(X1, YR1, YD1);)
CL = supF(Xk1), A(1)/(k)I(Xk1, Yk3)
I(X1;Y’, Ys) = H(Y’, Ys) − H(Y’, Ys|X1)
X1, X2, ... are i.i.d ~ N(0, P), and xi’ = d⋅yi’ where d is chossen to satisfy the relay power constraint
\mathchoiceX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + Zs
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)
I(X1;YD1YR1) = \mathchoiceH(YD1YR1)H(YD1YR1)H(YD1YR1)H(YD1YR1) − H(YD1YR1|X1) = H(YR1) + H(YD1|YR1) − H(YD1|X1) − H(YR1|X1YD1)
H(YR1) = H(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR) = (1)/(2)log(2πe)(b2d2a2P + b2d2N + N)
H(YD1|YR1) = H(X1 + Z|YR1) = (1)/(2)log(2πe)E(Var(X1 + Z|YR1)) = (1)/(2)log(2πe)⎛⎝P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N⎞⎠
E(Var(X1 + Z|YR1)) = E(Var(X1|YR1)) + N = P − (E2(X1⋅YR1))/(E(Y2R1)) + N = P − (E2(X1⋅(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR)))/(E(Y2R1)) + N = P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N
\mathchoiceH(YD1YR1)H(YD1YR1)H(YD1YR1)H(YD1YR1) = (1)/(2)log(2πe)(b2d2a2P + b2d2N + N) + (1)/(2)log(2πe)⎛⎝P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N⎞⎠ =
= (1)/(2)log(2πe)2(b2d2a2P + b2d2N + N)⋅⎛⎝P − (b2⋅d2⋅a2P2)/(b2d2a2P + b2d2N + N) + N⎞⎠ = (*)
(b2d2a2P + b2d2N + N)⋅⎛⎝P − (b2⋅d2⋅a2P2)/(b2d2a2P + b2d2N + N) + N⎞⎠ = (P + N)(b2d2a2P + b2d2N + N) − b2⋅d2⋅a2P2
Expand[(P + N)(b2d2a2P + b2d2N + N) − b2⋅d2⋅a2P2] = a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP
(*) = \mathchoice(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)
H(YD1|X1) = (1)/(2)log(2πe)(N)
H(YR1|X1YD1) = H(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR|X1YD1) = (1)/(2)log(b⋅d⋅Z1 + ZR|YD1) = = (1)/(2)log(b2⋅d2⋅N + N)
\mathchoiceI(X1;YD1YR1)I(X1;YD1YR1)I(X1;YD1YR1)I(X1;YD1YR1) = (1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP) − (1)/(2)log(2πe)2⋅N⋅(b2⋅d2⋅N + N) =
(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP) − (1)/(2)log(2πe)2⋅N⋅(b2⋅d2⋅N + N)
= (1)/(2)log((a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP))/(N⋅(b2⋅d2⋅N + N)) = (1)/(2)log\undersetA((a2b2d2NP + \cancelb2d2N2 + b2d2NP + \cancelN2 + NP))/(b2⋅d2⋅N2 + N2) = (*)
(*) = (1)/(2)⋅log⎛⎝1 + (P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ = \mathchoiceC⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ Q.E.D!!!
C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ = C⎛⎜⎝(P)/(N) + (a2b2)/((a2 + b2)(P)/(N) + 1)⋅(P2)/(N2)⎞⎟⎠ = C⎛⎝S31 + (S21⋅S32)/(S21 + S32 + 1)⎞⎠ Ова е во согласност со изразот од El Gamal NIT.
CL = supF(Xk1), A(1)/(k)I(Xk1, Yk3)
I(X1;Y’, Ys) = H(Y’, Ys) − H(Y’, Ys|X1)
X1, X2, ... are i.i.d ~ N(0, P), and xi’ = d⋅yi’ where d is chossen to satisfy the relay power constraint
\mathchoiceX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + ZsX1 ~ N(0, P) Y’ = a⋅X1 + Z1 X’ = d⋅Y’ YR = b⋅X’ + ZR = b⋅d⋅(a⋅X1 + Z1) + ZR = b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR Ys = YD1 = X1 + Zs
\mathchoiced = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)d = √((2αP)/(a22αP + N)) d2 = (P)/(a2P + N) = ((P)/(N))/(a2(P)/(N) + 1)
I(X1;YD1YR1) = \mathchoiceH(YD1YR1)H(YD1YR1)H(YD1YR1)H(YD1YR1) − H(YD1YR1|X1) = H(YR1) + H(YD1|YR1) − H(YD1|X1) − H(YR1|X1YD1)
H(YR1) = H(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR) = (1)/(2)log(2πe)(b2d2a2P + b2d2N + N)
H(YD1|YR1) = H(X1 + Z|YR1) = (1)/(2)log(2πe)E(Var(X1 + Z|YR1)) = (1)/(2)log(2πe)⎛⎝P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N⎞⎠
E(Var(X1 + Z|YR1)) = E(Var(X1|YR1)) + N = P − (E2(X1⋅YR1))/(E(Y2R1)) + N = P − (E2(X1⋅(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR)))/(E(Y2R1)) + N = P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N
\mathchoiceH(YD1YR1)H(YD1YR1)H(YD1YR1)H(YD1YR1) = (1)/(2)log(2πe)(b2d2a2P + b2d2N + N) + (1)/(2)log(2πe)⎛⎝P − (b2⋅d2⋅a2P)/(b2d2a2P + b2d2N + N) + N⎞⎠ =
= (1)/(2)log(2πe)2(b2d2a2P + b2d2N + N)⋅⎛⎝P − (b2⋅d2⋅a2P2)/(b2d2a2P + b2d2N + N) + N⎞⎠ = (*)
(b2d2a2P + b2d2N + N)⋅⎛⎝P − (b2⋅d2⋅a2P2)/(b2d2a2P + b2d2N + N) + N⎞⎠ = (P + N)(b2d2a2P + b2d2N + N) − b2⋅d2⋅a2P2
Expand[(P + N)(b2d2a2P + b2d2N + N) − b2⋅d2⋅a2P2] = a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP
(*) = \mathchoice(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP)
H(YD1|X1) = (1)/(2)log(2πe)(N)
H(YR1|X1YD1) = H(b⋅d⋅a⋅X1 + b⋅d⋅Z1 + ZR|X1YD1) = (1)/(2)log(b⋅d⋅Z1 + ZR|YD1) = = (1)/(2)log(b2⋅d2⋅N + N)
\mathchoiceI(X1;YD1YR1)I(X1;YD1YR1)I(X1;YD1YR1)I(X1;YD1YR1) = (1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP) − (1)/(2)log(2πe)2⋅N⋅(b2⋅d2⋅N + N) =
(1)/(2)log(2πe)2(a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP) − (1)/(2)log(2πe)2⋅N⋅(b2⋅d2⋅N + N)
= (1)/(2)log((a2b2d2NP + b2d2N2 + b2d2NP + N2 + NP))/(N⋅(b2⋅d2⋅N + N)) = (1)/(2)log\undersetA((a2b2d2NP + \cancelb2d2N2 + b2d2NP + \cancelN2 + NP))/(b2⋅d2⋅N2 + N2) = (*)
A = 1 + ((a2b2d2NP + b2d2NP + NP))/(b2⋅(P)/(a2P + N)⋅N2 + N2) = 1 + (((a2 + 1)b2d2NP + NP))/(N2⎛⎝b2⋅(P)/(a2P + N) + 1⎞⎠) = 1 + (NP((a2 + 1)b2d2 + 1))/(N2⎛⎝(b2P + a2P + N)/(a2P + N)⎞⎠) = 1 + (P⎛⎝(a2 + 1)b2(P)/(a2P + N) + 1⎞⎠)/(N⎛⎝(b2P + a2P + N)/(a2P + N)⎞⎠) =
= 1 + (P⎛⎝((a2 + 1)b2⋅P + a2P + N)/(a2P + N)⎞⎠)/(N⎛⎝(b2P + a2P + N)/(a2P + N)⎞⎠) = 1 + (P((a2 + 1)b2⋅P + a2P + N))/(N(b2P + a2P + N)) = 1 + (P)/(N)⋅((a2b2⋅P + \cancelb2⋅P + a2P + N))/((b2P + a2P + N)) = 1 + (P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠
(*) = (1)/(2)⋅log⎛⎝1 + (P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ = \mathchoiceC⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ Q.E.D!!!
C⎛⎝(P)/(N)⋅⎛⎝1 + (a2b2⋅P)/((a2 + b2)P + N)⎞⎠⎞⎠ = C⎛⎜⎝(P)/(N) + (a2b2)/((a2 + b2)(P)/(N) + 1)⋅(P2)/(N2)⎞⎟⎠ = C⎛⎝S31 + (S21⋅S32)/(S21 + S32 + 1)⎞⎠ Ова е во согласност со изразот од El Gamal NIT.
C = I(X1;YD1YR1)
Cutset bound:
maxp(x1x2)min{{I(X1, X2;Y3), I(X1;Y2Y3|X2)}}
I(X1X2;Y3) = H(Y3) − H(Y3|X1X2)
7.3 Капацитет на засили и проследи без директна компонента
Капацитеот за овој тип на канал може да се добие од општиот изараз за AaF ако земе S31 = 0:
Истиот израз може да се добие на следниов начин:
z ~ N(0, N) z1 ~ N(0, N1)
y1 = h0x1 + z1 y2 = h2x2 + z γ0 = (|h0|2)/(N1) γ1 = (|h1|2)/(N) γ2 = (|h2|2)/(N)
Bез директна компонента:
ŷ1 = √((P2)/(h20P1 + N1))y1 = h0√((P2)/(h20P1 + N1))x1 + √((P2)/(h20P1 + N1))z1 y2 = h2ŷ1 + z = h2⋅h0⋅√((P2)/(h20P1 + N1))x1 + h2⋅√((P2)/(h20P1 + N1))z1 + z
I(X1;Y2) = h(Y2) − h(Y2|X1) = h(h2⋅h0⋅√((P2)/(h20P1 + N1))x1 + h2⋅√((P2)/(h20P1 + N1))z1 + z) − h(Z1 + Z) =
= (1)/(2)log2πe⎛⎝h22⋅h20⋅(P2)/(h20P1 + N1)P1 + (h22⋅P2)/(h20P1 + N1)⋅N1 + N⎞⎠ − (1)/(2)log2πe⋅⎛⎝(h22⋅P2N1)/(h20P1 + N1) + N⎞⎠
= (1)/(2)log(h22⋅(h20)/(N1)⋅(P2)/(γ0P1 + 1)⋅P1 + (h22⋅P2)/(h20P1 + N1)⋅N1 + N)/(⎛⎝N1⋅(h22P2)/(h20P1 + N1) + N⎞⎠) = (1)/(2)log⎛⎜⎜⎜⎝1 + ((h22⋅P2⋅γ0⋅P1)/(γ0P1 + 1))/(N⋅⎛⎜⎝((h22)/(N)P2)/(γ0P1 + 1) + 1⎞⎟⎠)⎞⎟⎟⎟⎠ =
(1)/(2)log⎛⎝1 + (γ2⋅P2⋅γ0⋅P1)/(γ2P2 + γ0P1 + 1)⎞⎠
8 Channel Cappacity of MIMO Relay Channel
8.1 B. Badic Space-Time Block Coding for Multiple Antenna Systems
The capacity of deterministic SISO channel with an input-output relation r = H⋅s + n is given by:
where the normalized channel power transfer characteristic is |H|2 . The average SNR at each receiver branch independent on nt is ρ = P ⁄ σ2n and the P is the average power at the output of each receive antennas. the channel capacity of deterministic MIMO channl is given by [3]
and for random MIMO channels, the mean channel capacity, asp called the ergodic capacity is given by [2]:
where EH denotes expectation with respect to H. The ergodic capacity grows with the nuber of n of antennas (under the assumption nt = nr = n) which results in a significant capacity gain of MIMO fading channles compared to a wireless SISO transmission.
8.1.1 Capacity of Orhogonal STBC vs. MIMO Channel Capacity
The design of STBCs that are capable of approaching the capacity of MIMO systems is a challenging problem and of high importance. The alamouti code is suitabel to achieve the channel capacity in the case of two transmit and one receive antennas. However, no such scheme is known for more than two transmit antennas.
In [4] it has been shown that OSTBs can achieve the maximum information rate only wehn the receiver has only one receive antenna. That means, that in general OSTBCs can never reach the cpaacity of MIMO channle. We proof that in the following.
If we denote the variance of the transmitted symbol as σ2s the overall energy necessary to transmit the space-time code S is:
where nN is a number of symbols different from zero that are transmitted on each antenan with N time slots. If the STBC spans over N time slots, the average power per time slots is
Овде подобро да го изразиш σ2s, за да бидам во согласност со моите изрази во тезата во глава 2
:
(8) Ps = (ntnNσ2s)/(N)
Во моите чланци т.е. глава 2, 3, 4 ја користам следнава дефиниција
Изворот S испраќа со моќност P
Ова е per time slot. Нормално снагата се дефинира по единица време!!!
и нема директната комуникација меѓу изворот и дестинацијата. Употребуваните OSTBC кодови се означуваат како кодови со три цифри, NKL, каде N е борјот на антени, K е бројот на кодни симболи испратени во еден коден блок, и L претставува број на потребни временски слотови за испраќање на еден коден збор
Средната снага по симбол е:
E = P⋅c, c = (L)/(K N )
Значи важи следнава паралела на означување
E≜σ2s nN = K nt = N N = L
E = P⋅c, c = (L)/(K N )
Значи важи следнава паралела на означување
E≜σ2s nN = K nt = N N = L
Значи изразот 8↑ со моите ознаки ќе биде:
P = (K⋅N)/(L)⋅E
Assuming that the OSTBC transmits nN information symbols within N time slots, the maximum achievable capacity of OSTBC conditioned to the channel H is achieved with uncorrelated input signal and results in [2]:
Using the singular value decomposition approach H⋅HH = U⋅Λ⋅UH, capacity in 9↑ can be rewriten as:
On the other side, the capacity of the equivalent MIMO channel without channel knowledge at the transmitter for a given channel relaization is:
(11) CMIMO = log2det⎛⎝Inr + (Ps)/(ntσ2n)⋅H⋅HH⎞⎠ = r⎲⎳i = 1log2⎛⎝1 + (Ps)/(ntσ2n)⋅λi⎞⎠ bit/channel use
Second expression in 11↑ is obtained using the singular value decomposition approach, where λi are positive eigenvaulues of the H⋅HH and r is rank of the channel matrix H. From this we can see that the MIMO channel capacity corresponds to the sum of the capacities of a SISO channels, each having a power gain of λi and transmit power Ps ⁄ nt ([5]).
The loss in capacity between a MIMO channel and an OSTBC transmission with nN ≤ N is:
COSTBC − CMIMO = (nN)/(N)log2⎛⎝1 + (N⋅Ps)/(nN⋅nt⋅σ2n)⋅r⎲⎳i = 1λi⎞⎠ − r⎲⎳i = 1log2⎛⎝1 + (Ps)/(ntσ2n)⋅λi⎞⎠ = (nN)/(N)⋅log2⎛⎜⎝1 + (Ps)/((nN)/(N)⋅nt⋅σ2n)⋅r⎲⎳i = 1λi⎞⎟⎠ − r⎲⎳i = 1log2⎛⎝1 + (Ps)/(ntσ2n)⋅λi⎞⎠ ≤
(b) folows from a⋅log(1 + x ⁄ a) ≤ log(1 + x) 0 < a ≤ 1 x > 0
Jensen
E[f(x)] ≥ f(E[x]) ако f(x) e конвексна функција
Ако f(x) е конкавна (каква што е log(...))
E[f(x)] ≤ f(E[x])
E[f(x)] ≥ f(E[x]) ако f(x) e конвексна функција
Ако f(x) е конкавна (каква што е log(...))
E[f(x)] ≤ f(E[x])
(13) COSTBC − CMIMO\overset(c) ≤ r⎲⎳i = 1log2⎛⎝1 + (Ps)/(nt⋅σ2n)⋅λi⎞⎠ − r⎲⎳i = 1log2⎛⎝1 + (Ps)/(ntσ2n)⋅λi⎞⎠ ≤ 0
(c) folows from
Пази нека не те буни ова не е Јансен неравенството. Во Јансен неравенството имаш средни вредности, а овде немаш. види Мапле MIMO Capacity.mw.
log(1 + ⎲⎳ixi) ≤ ⎲⎳ilog(1 + xi)
The equality sign in 13↑ hold true if and only if nN = N and the channel rank is one r = 1. This conditon is only fulfilled by the Alamouti full rate, full diversity code. Therefore, we can conclude that the orthogonal design cannot reach the MIMO channel capacity, except fo the case when nn = N and the channel rank is one.
For the case of a MISO system (nr = 1, nt > nr), the channel matrix is a row matrix H = [h1, h2, ..., hnt]. With H⋅HH = ∑ntj = 1|hj|2 , equation 11↑ специализес то:
8.1.2 Capacity of QSTBC with No Channel State Information at the Transmitter
Since we know that the eigenvalues of a QSTBC induced equivalietn virtual channel matrix Hv are
where
capacity of the QSTBC for four transmit antxennas (when the channel is unknown at the transmitter) can be writen as:
(18) = (1)/(2)⋅⎧⎩log2⎛⎝1 + (Ps)/(4σ2n)h2(1 + X)⎞⎠ + log2⎛⎝1 + (Ps)/(4σ2n)h2(1 − X)⎞⎠⎫⎭bits/channel use
COSTBC = (nN)/(N)log2det⎛⎝1 + (N⋅Ps)/(nN⋅nt⋅σ2n)⋅||H||2⎞⎠ = (4)/(4)log2det⎛⎝1 + (4⋅Ps)/(4⋅4⋅σ2n)⋅||H||2⎞⎠ = log2det⎛⎝1 + (Ps)/(4⋅σ2n)⋅||H||2⎞⎠
If the channel dependent interference parameter X vanishes, the channel capacity of a QSTBC scheme becomes
This is the ideal Channel capacity of a rate-one orthogonal STBC for four transmit antennas and one receive antenna with uniformly distributed signal power and a given channel realization [4]. However such a rate-one code does not exist for an open-loop transmission scheme with more than two transmit antennas. Therefore a QSTBC for four transmit antennas and using one receive antenna cannot reach the MISO channel capacity 14↑.
8.1.3 Capacity of QSTBC with Channel State Information at the Transmitter
When partial CSI is returned to the transmitter the QSTBC performeance can be substentionally improved. For closed-loop transmission schemes, the cannel dependent interference parametr X is approximately zero. Thus the channel capacity for QSTBC in code selection transmission scheme wiht X ≈ 0 can be writen as:
and for the space-time coded transmission in antenna selected MIMO system gain, with X ≈ 0 and h2sel = ∑jmax|hj|2, j = 1, 2, ..4 the channel capacity is given by:
where h2sel is the channel gain form the optimum selected antenna subset. From the equation 21↑ it is obvious that the cahnnel capacity of QSTBC with CSI is equal to the MISO channel capacity without CSI.
8.2 B. Holter Capacity of MIMO
If the signal at the destination of the MIMO point-to-point system is:
(22) Y = H⋅X + N
and h(...) denote differential entropy , the mutual information of MIMO system can be expressed as:
I(X;Y) = h(Y) − h(Y|X) = h(Y) − h(Y|X) = h(Y) − h(H⋅X + N|X) = h(Y) − h(N|X) = h(Y) − h(N)
Assuming N ~ N(0, Kn), where Kn is noise covariance matrix. Since the normal distribution maximizes the entrop over all distributions with the smae covariance (i.e. power constraint), the mutual information is maximized when Y represents a multivariate Gaussian random variable.
With the assumtion that X and N are independent the received signal covariance matrix Ky may be expressed as:
E[Y⋅YH] = E[(H⋅X + N)⋅(H⋅X + N)H]
E[(H⋅X + N)⋅(H⋅X + N)H] = E[(H⋅X + N)⋅(XH⋅H + NH)] = E[(H⋅X + N)⋅(XH⋅HH + NH)]
where Kn = E[X⋅XH]
If we replace 23↑ in 22↑, use [1] and distributive law for determinatns, we obtain the channel capacity:
C = h(Y) − h(N) = log[det(2πe(H⋅Kx⋅HH + Kn))] − log2det(2πe⋅Kn) = log[det((H⋅Kn⋅HH + Kn)⋅K − 1 n)]
When the transmitter has no knowledge of the channel, it is optimal to evenly distribute the available power PT among the transmit antennas, i.e. , Kx = (PT)/(nT)InT. Дополнително, ако се претпостави дека шумот во антените не е корелиран, матрицата на коваријанси за шумот е: Kn = σ2nInR. Во ваков случај капацитето на MIMO системот се сведува на:
By the law of large numbers, the term (1)/(nT)H⋅HH → InR as nT gets large and nR is fixed, thus the capacity in he limit of large nT is:
Further analysis of the MIMO channel capacity is possible by diagonalizing the product matrix H.HH eather by eigenvalue decomposition or singular value decomposition.
- Eigenvalue decomposition of the matrix product H⋅HH = E⋅Λ⋅EH
where E is the eigenvector matrix with orthonormal colums and and Λ is a diagonal matrix with the eigenvalues on the main diagonal.
- Singular value decomposition of the channel matrix H = U⋅Σ⋅VH
where U and V are unitary matrices of left and right singular vectors respectively, and Σ is diagonal matrix with singular values on the main diagonal.
U⋅Σ⋅VH.(U⋅Σ⋅VH)H = U⋅Σ⋅VH.(Σ⋅VH)HUH = U⋅Σ⋅VH.(VH)H⋅ΣH⋅UH
- Има убава реченица во чланакот од Кафеџиски за корелираност на сигналите во релеен систем. Таа многу кажува како да ги решаваш проблемите каде имаш математички операции и барање на варијанса на сигнали со повеќе случајни променливи.
2. За MIMO капацитет многу добар уводен чланак ми изгледа [3], а богами и [2]. Овој вториов има над 10.000 референци на GS.
3. Зошто во изразот за капацитет со матрици нема (1)/(2) пред логаритамот?
References
[1] T. M. Cover, J. A. Thomas, Elements of Information Theory, Second Edition, John Wiley & Sons, 2006.
[2] I.E. Telatar, Capacity of Multi-Antenna Gaussian Channels, Eropean transactions on telecommunications, 1999
[3] [2] G. J. Foschini, M. J. Gans, “On Limits of Wireless Communications in Fading Environments when Using Multiple Antennas”, Wireless Personal Communications, vol. 6, pp. 311-335, March 1998.
[4] S. S. Paulraj, ”Space-Time Block Codes: a capacity perspective”, IEEE Communications Letters, vol. 4, pp. 384-386, Dec. 2000.
[5] [38]B. Vucetic, J. Yuan, ”Space-Time Coding”, John Wiley & Sons, England, 2003.
[6] S. S. Paulraj, ”Space-Time Block Codes: a capacity perspective”, IEEE Communications Letters, vol. 4, pp. 384-386, Dec. 2000.