\sloppy

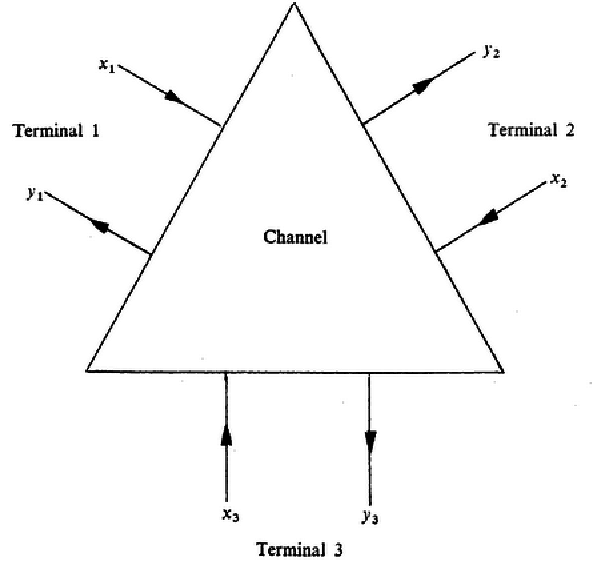
Three terminal communication channel (van der Meulen)

1 Introduction

Figure 1 Three-terminal communication channel

Formally, a discrete memoryless (d.m) three-terminal channel, denoted by P(y₁, y₂, y₃|x₁, x₂, x₃) consist of three pairs (A_t, B_t) of finite sets having a_t ≥ 2, b_t ≥ 2 elements, respectively, and a collection of probability distributions on B₁xB₂xB₃, one for each input (x₁, x₂, x₃) ∈ A₁xA₂xA₃, such that

(1) P(y₁, y₂, y₃|x₁, x₂, x₃) = ⁿ∏_k = 1P(y_1k, y_2k, y_rk|x_1k, x_2k, x_3k)

2 Transmission along subchannels

Consider now the problem of sending information at a positive rate from terminal 1 to terminal 3, say, through a channl which has three different terminals. We are interested in determining which is the best way, i.e., what is the highest rate that can be achieved for sending in the 1-3 direction with arbitrary small probability of error.

A subchannel is a one-way channel which can be derived form the channel P(y₁, y₂, y₃|x₁, x₂, x₃) by keeping the input letter at one or two terminals fixed and by varying the inputs at the remaining terminals. We only consider those sub-channels which can be used to send information away from terminal 1, or to send information into terminal 3.

Definitions of five different subchannels

Let channel \strikeout off\uuline off\uwave offP(y₁, y₂, y₃|x₁, x₂, x₃) be given. We consider five kinds of subchannels:

(i) For each fixed pair (x₂, x₃) for inputs define a discrete memoryless one-way channel (d.m.c) \strikeout off\uuline off\uwave offP(y₃|x₁|x₂, x₃) with inputs x₁ and outputs y₃ by:\uuline default\uwave default

(2) P(y₃|x₁|x₂, x₃) = ⎲⎳_y₁, y₂P(y₁, y₂, y₃|x₁, x₂, x₃)

Let C₁(1, 3|x₂, x₃) be its capacity and C₁(1, 3) = max_x₂, x₃C₁(1, 3|x₂, x₃).

(ii) Similarly

(3) P(y₂|x₁|x₂, x₃) = ⎲⎳_y₁, y₃P(y₁, y₂, y₃|x₁, x₂, x₃)

Let C₁(1, 2|x₂, x₃) be its capacity and C₁(1, 2) = max_x₂, x₃C₁(1, 2|x₂, x₃).

(iii) For each pair (x₂, x₃) define a d.m.c P(y₂, y₃|x₁|x₂, x₃) with inputs x₁ and pair of outputs (y₂, y₃) by:

(4) P(y₂, y₃|x₁|x₂, x₃) = ⎲⎳_y₁, y₃P(y₁, y₂, y₃|x₁, x₂, x₃)

Denote its capacity with C₁[1, (2, 3)|x₂, x₃] and define:

(5) C₁[1, (2, 3)] = max_x₂, x₃C₁[1, (2, 3)|x₂, x₃]

(iv) For each fixed pair (x₁, x₃) define a d.m.c \strikeout off\uuline off\uwave offP(y₃|x₂|x₁, x₃) with inputs x₂ and outputs y₃ by:

(6) P(y₃|x₂|x₁, x₃) = ⎲⎳_y₁P(y₁, y₂, y₃|x₁, x₂, x₃)

Let C₁(2, 3|x₁, x₃) be its capacity and C₁(2, 3) = max_x₁, x₃C₁(2, 3|x₁, x₃)

(v) For each fixed input letter x₃ define a d.m.c \strikeout off\uuline off\uwave offP(y₃|x₁, x₂|x₃) with pairs of inputs (x₁, x₂) and outputs y₃ by:

(7) P(y₃|x₁, x₂|x₃) = ⎲⎳_y₁, y₂P(y₁, y₂, y₃|x₁, x₂, x₃)

Denote its capacity with C₁[(1, 2), 3|x₂, x₃] and define:

(8) C₁[(1, 2), 3] = max_x₂, x₃C₁[(1, 2), 3|x₂, x₃]

To each of the above subchannels we have associated a channel capacity. This means one may apply the fundamental coding theorem for a d.m. channel which was first formulated by Shannon. It states that one may transmit over the channel at a rate arbitrarily close to the capacity with arbitrarily small probability of error by using the channel sufficiently many times.

The operation of a channel of the form P(y₂, y₃|x₁|x₂, x₃) may be interpreted as follows. Imagine terminals 2 and 3 located at the same place. A pair of symbols (y₂, y₃) then becomes a single output to the channel. Interpreted this way, the d.m.c \strikeout off\uuline off\uwave offP(y₂, y₃|x₁|x₂, x₃) can be used to send information form terminal 1 o the \uuline default\uwave defaultpair\strikeout off\uuline off\uwave off of terminals (2,3).

3 Examples of three-terminal channels

Figure 2 Example of three terminal channel

Example 1

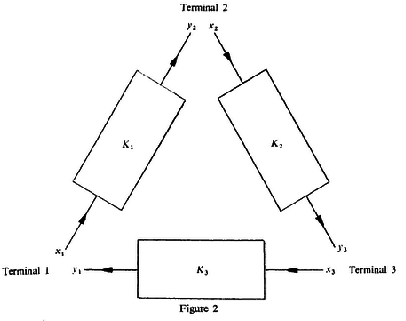
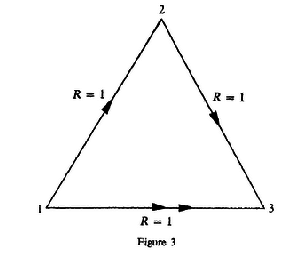
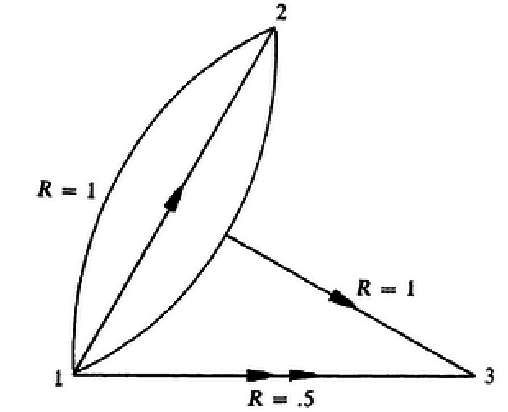
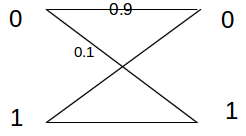
In 2↑ the three-terminal channel decomposes into three independent noiseless one-way channels with binary inputs and outputs. The operation of the channel is: y₂ = x₁; y₃ = x₂; y₁ = x₃; . The problem is how to comunicate form Therminal 1 to Therminal 3 as effectively as posible. Since y₃ = x₂ the inputs x₁ at thermonal 1 cannot influence the outputs at y₃ into one single opration i.e. C₁(1, 3) = 0. However, terminal 1 can transmit at rate one to terminal 2 using channel K₁ and terminal 2 can send at rate one to terminal 3 using channel K₂. Thus terminal 1 can transmit information to terminal 3 by first sending to teminal 2 who then sends the recieved infomation on to terminal 3. In fact, since the operations of channels K₁ and K₂ are independent, terminal 1 and terminal 2 can transmit simultaneosuly and therefore terminal 1 can sent to terminal 3 at rate arbitrary close to one with zero error probability by using blocks of sufficient length n (MMV).

Figure 3 Example of three terminal channle

We have sumarized this results in 3↑. The double arrow indicates that a rate arbitrarry close to one in the 1-3 direction can be attained only if two channel operatios are allowed for the transmission of each single letter form terminal 1 to terminal 3.

Example 2

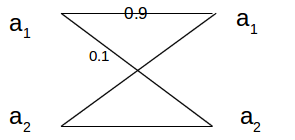
(4↓) is generalization of an example given by Shannon [6] of a two-way channel, so-called modulo2 adder.

Figure 4 Example 2 of three terminal cahnnel

The inputs and outputs at each terminal are again x₁ + x₂ = y₂(mod 2) x₂ + x₃ = y₃(mod 2) x₁ + x₃ = y₁(mod 2) . As the previous example, this three-terminal channl can be thougth as composed of three independent one-way noisless binary channels. In order to determine at terminal 2 the transmitted x₁ one needs to add (mod 2) the just transmitted x₂ to the observed y₂. To each input letter x₂ there corresponds a noisless one-way channel for sending from terminal 1 to terminal 3. Thus terminal 1 can send at rate one to terminal 2 and independently terminal 2 can send at rate one to treminal 3, i.e., C₁(1, 2) = C₁(2, 3) = 1. But then again terminial 1 can send to terminal 3 at rate arbitrary close to one with zero error probability, by first sending information at rate one to terminal 2 who then sends this information at the same rate on to terminal 3 (суштината е што терминал 2 не чека цела поворка да ја прати тој прима и одма праќа, само за првиот симбол имаш доцнење, другите одат едно за друго). As in the previous example it is not possible for the inputs at terminal 1 to influence the outpust at terminal 3 in one single transmission period, i.e., C₁(1, 3) = 0.

Example 3

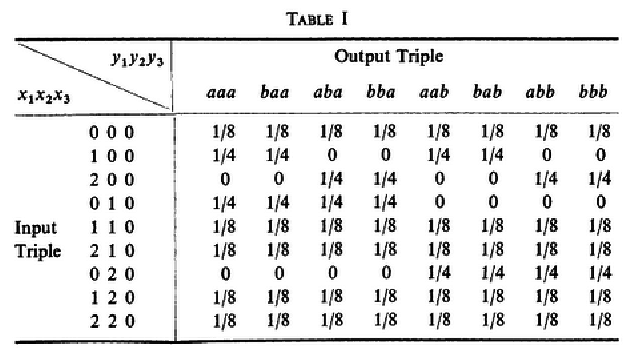
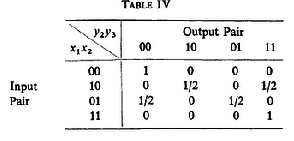
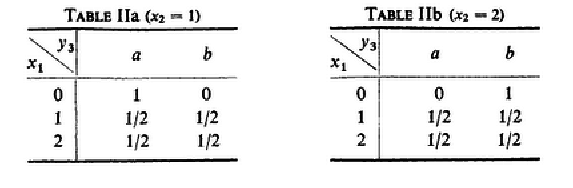
In the third example terminal 1 can choose between two different methods Двата примери во Example3 се: 1. Праќаш од 1-3 2. Праќаш од 1-2 па потоаа од 2-3 for transmitting information to terminal 3. Here the input letters x₁, x₂, and x₃ all belong to a ternary alphabet whereas the output letter y₁, y₂, y₃ are all binary. Suppose that channel probabilities \strikeout off\uuline off\uwave offP(y₁, y₂, y₃|x₁, x₂, x₃) \uuline default\uwave defaultare the same for different x₃\strikeout off\uuline off\uwave off and are given by Table I.

Table 1 Probabilities

The corresponding marginal conditional probabilities P(y₃|x₁|x₂) for sending from terminal 1 to terminal 3 if x₂ is held at the letters 1 or 2 respectively are given in Tables IIa and IIb (овие табели се изведени директно од 1↑ само ги набљудуваш оние колони од табелтата за кои x₂ одговара на зададената вредност).

Table 2 Marginal Conditional probabilities

-Иницијални изведувања:

P(y₃|x₁ = 0|x₂ = 1) = ^b⎲⎳_y₃ = ap(Y₃, X₁ = 0, x₂ = 1) = 1 + 0 = 1

\strikeout off\uuline off\uwave off

P(y₃|x₁ = 1|x₂ = 1) = ^b⎲⎳_y₃ = ap(Y₃, X₁ = 0, x₂ = 1) = (1)/(2) + (1)/(2) = 1

P(y₃|x₁ = 2|x₂ = 1) = ^b⎲⎳_y₃ = ap(Y₃, X₁ = 2, X₂ = 1) = (1)/(2) + (1)/(2) = 1

P(x₁, y₃|x₂ = 1) = p(x₁ = 0)⋅P(y₃|x₁ = 0|x₂ = 1) + p(x₁ = 1)⋅P(y₃|x₁ = 1|x₂ = 1) + p(x₁ = 2)⋅P(y₃|x₁ = 2|x₂ = 1) = p(x₁) + p(x₂) + p(x₃) = 1

P(x₁, y₃|x₂ = 2) = p(x₁ = 0)⋅P(y₃|x₁ = 0|x₂ = 2) + p(x₁ = 1)⋅P(y₃|x₁ = 1|x₂ = 2) + p(x₁ = 2)⋅P(y₃|x₁ = 2|x₂ = 2) = p(x₁) + p(x₂) + p(x₃) = 1

P(x₁, x₂, y₃) = p(x₂ = 1)⋅P(x₁, y₃|x₂ = 1) + p(x₂ = 2)⋅P(x₁, y₃|x₂ = 2) = p(x₁) + p(x₂) + p(x₃) = 1

C = max[H(Yⁿ) − H(Yⁿ|Xⁿ)] = log(8) + ⎲⎳_{(x₁x₂x₃;y₁, y₂, y₃)}P(Xⁿ)P(Yⁿ|Xⁿ)⋅log(P(Yⁿ|Xⁿ))

− H(Yⁿ|Xⁿ) = 5⋅8⋅(1)/(64)⋅log((1)/(8)) + 4⋅4⋅(1)/(32)⋅log((1)/(4)) = 2.875
C = max[H(Yⁿ) − H(Yⁿ|Xⁿ)] = log₂(8) − 2.875 = 0.125
C₁ = (max[H(Yⁿ) − H(Yⁿ|Xⁿ)])/(3) = 0.0416666667 bits ⁄ transmission

-Во боксот долу се навраќам на два проблеми од книгата на Cover

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~recall from Textbook figure TextbookProblem7.13.png

I(X₁, X₂;Y₁, Y₂) = ?
X₁, X₂|Y₁Y₂ 01 10 11 00 00 1 0 0 0 01 0 1 0 0 10 0 0 1 0 11 0 0 0 1

\strikeout off\uuline off\uwave offI(X₁, X₂;Y₁, Y₂) = H(Y₁, Y₂) − H(Y₁, Y₂|X₁X₂) = H(X₁, X₂) − H(X₁, X₂|Y₁Y₂)

C=max(I(X₁, X₂;Y₁, Y₂)) = log₂(4) − 0 = 2 bits
(X₁, X₂) ∈ [00, 01, 10, 11] p(X₁, X₂) = [(1)/(4), (1)/(4), (1)/(4), (1)/(4)]
I(X₁;Y₁) = H(Y₁) − H(Y₁|X₁) = log(2) − H(Y₁|X₁) uniform input distribution of symbols maximizes the entropy ⇒ output symbols are also uniformely distributed

\strikeout off\uuline off\uwave offH(Y₁|X₁) = ∑p(x₁)⋅p(y₁|x₁)⋅log₂(p(y₁|x₁))

(a) Crossover probability

000 001 010 100 → a₁ 111 110 101 011 → a₂
⎛⎜⎝ 3 2 ⎞⎟⎠ = (3!)/(2!) = (6)/(2) = 3 P(ϵ) = q = 1 − p P(ϵ) = p
Crossover probability is:
P(a₂|a₁) = ∑³_i = 2⎛⎜⎝ 3 i ⎞⎟⎠⋅qⁱ⋅p^i − 1 = ⎛⎜⎝ 3 2 ⎞⎟⎠⋅q²⋅p¹ + ⎛⎜⎝ 3 3 ⎞⎟⎠⋅q³ = 0.0280000000

(b) Capacity of the channelI(X;Y) = H(Y) − H(Y|X); C = log₂(2) − H(Y|X)

\strikeout off\uuline off\uwave offH(Y|X) = P(000)⋅H(Y|000) + P(111)⋅H(Y|111) = 1 = P(a₁)(0.028⋅log₂(0.028) + .972⋅log₂(.972)) + P(a₂)(0.028⋅log₂(0.028) + .972⋅log₂(.972)) = 0.1842605934

\strikeout off\uuline off\uwave offC₃ = log₂(2) − H(Y|X) = 1 − 0.1842605934 = 0.8157394066

C = (C₃)/(3) = (0.8157394066)/(3) = 0.2719131355333
(0.8157394066)/(3) = 0.2719131355333;

(c) Original BSC

C = 1 − H(Y|X) = 1 − H(p) = 1 − 0.4689955936; 1 − 0.4689955936 = 0.5310044064
0.1log₂(0.1) + 0.9log₂(0.9) = − 0.4689955936

(d) Proof for any channel

I(Xⁿ;Yⁿ) = H(Yⁿ) − H(Yⁿ|Xⁿ) = H(Yⁿ) − ∑ⁿ_i = 1H(Y_i|Y^i − 1₁, Xⁿ) ≤ |conditioning reduces entropy| ≤ ∑ⁿ_i = 1H(Y_i) − ∑ⁿ_i = 1H(Y_i|Y^i − 1₁, Xⁿ)
= ∑ⁿ_i = 1H(Y_i) − ∑ⁿ_i = 1H(Y_i|X_i) =
= n⋅I(X;Y) ⇒ I(Xⁿ;Yⁿ) ≤ n⋅I(X;Y) (I(Xⁿ;Yⁿ))/(n) ≤ I(X;Y) ⇒ (C(Xⁿ, Yⁿ))/(n) ≤ C(X, Y)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

-Повторно изведување во врска тврдењето во чланакот дека капацитетот на каналот е 0.32. Јас добивам дека е 0.28.

I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂); C = log(2) − H(Y|X₁X₂); H(Y|X₁X₂) = ?
p(x_i = i) = p_i, i = 0, 1, 2; p(y = a) = p(a); p(y = b) = p(b)

1H(Y|X₁X₂) = p(x₂ = 1)⋅H(Y|X₁, X₂ = 1) + p(x₂ = 2)⋅H(Y|X₁, X₂ = 2) = − p(x₂ = 1)⋅{p(a|p₀)log₂p(a|p₀) + p₁⋅[p(a|p₁)⋅log₂p(a|p₁) + p(b|p₁)⋅log₂p(b|p₁)] + p₂⋅[p(a|p₂)log₂(p(a|p₂)) + p(b|p₂)log₂(p(b|p₂))]} − p(x₂ = 2){p(b|p₀)log₂p(b|p₀) + p₁⋅[p(a|p₁)⋅log₂p(a|p₁) + p(b|p₁)⋅log₂p(b|p₁)] p₂⋅[p(a|p₂)log₂(p(a|p₂)) + p(b|p₂)log₂(p(b|p₂))]} = p(x₂ = 1){p₁ + p₂} + p(x₂ = 2){p₁ + p₂} = p₁ + p₂

\strikeout off\uuline off\uwave offH(Y|X₁X₂) = p(X₂ = 1){0 + p(X₁ = 1)⋅1 + p(X₁ = 2)⋅1} + p(X₂ = 2){0 + p(X₁ = 1)⋅1 + p(X₁ = 2)⋅1} = p(X₁ = 1) + p(X₁ = 2)

I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = H(Y) − (p(X₁ = 1) + p(X₁ = 2))
C = log₂(2) − (p(X₁ = 1) + p(X₁ = 2)) = | unifrom output symbols implay uniform inputs| = 1 − (2)/(3) = 0.33

y₃|x₁x₂x₃ a b 000 1 ⁄ 2 1 ⁄ 2 100 1 ⁄ 2 1 ⁄ 2 200 1 ⁄ 2 1 ⁄ 2 010 1 0 110 1 ⁄ 2 1 ⁄ 2 210 1 ⁄ 2 1 ⁄ 2 020 0 1 120 1 ⁄ 2 1 ⁄ 2 220 1 ⁄ 2 1 ⁄ 2 \strikeout off\uuline off\uwave off y₂|x₁x₂x₃ a b 000 1 ⁄ 2 1 ⁄ 2 100 1 0 200 0 1 010 1 ⁄ 2 1 ⁄ 2 110 1 ⁄ 2 1 ⁄ 2 210 1 ⁄ 2 1 ⁄ 2 020 1 ⁄ 2 1 ⁄ 2 120 1 ⁄ 2 1 ⁄ 2 220 1 ⁄ 2 1 ⁄ 2 y₁|x₁x₂x₃ a b 000 1 ⁄ 2 1 ⁄ 2 100 1 ⁄ 2 1 ⁄ 2 200 1 ⁄ 2 1 ⁄ 2 010 1 ⁄ 2 1 ⁄ 2 110 1 ⁄ 2 1 ⁄ 2 210 1 ⁄ 2 1 ⁄ 2 020 1 ⁄ 2 1 ⁄ 2 120 1 ⁄ 2 1 ⁄ 2 220 1 ⁄ 2 1 ⁄ 2

H(Y₃|X₁X₂X₃) = H(Y₃|X₁X₂) = p(000)⋅1 + p(100)⋅1 + p(200)⋅1 + p(010)⋅0 + p(110)⋅1 + p(210)⋅1 + p(020)⋅0 + p(120)⋅1 + p(220)⋅1
C = H(Y₃) − H(Y₃|X₁X₂X₃) = 1 − H(Y₃|X₁X₂) = 1 − 7 ⁄ 9 = (2)/(9)

\strikeout off\uuline off\uwave offH(Y₁|X₁X₂X₃) = H(Y₃|X₁X₂) = p(000)⋅1 + p(100)⋅1 + p(200)⋅1 + p(010)⋅1 + p(110)⋅1 + p(210)⋅1 + p(020)⋅1 + p(120)⋅1 + p(220)⋅1 = 1

\strikeout off\uuline off\uwave offH(Y₂|X₁X₂X₃) = H(Y₃|X₁X₂) = p(000)⋅1 + p(100)⋅0 + p(200)⋅0 + p(010)⋅1 + p(110)⋅1 + p(210)⋅1 + p(020)⋅1 + p(120)⋅1 + p(220)⋅1 = 1

C₁(1, 3) = max_x₂, x₃C₁(1, 3|x₂, x₃) ова е од дефиницијата во чланакот на van der Meulen

\strikeout off\uuline off\uwave offP(y₃|x₁|x₂, x₃) = ∑_y₁, y₂P(y₁, y₂, y₃|x₁, x₂, x₃)

C₁(1, 3) = max[I(X₁;Y₃)] = H(Y₃) − H(Y₃|X₁) = log₂(2) − p(x₁ = 0)⋅0 − p(x₂ = 1)⋅1 − p(x₁ = 2)⋅1 = 1 − p(x₁ = 1) − p(x₁ = 2)
Значи и без да усреднуваш по x₂ го добивам истиот резултат за капацитетот.

Сега ќе одам со Лагранжови мултипликатори

y₃|x₁ a b 0 1 0 1 0.5 0.5 2 0.5 0.5 (x₁, y₃) a b p(x₁) 0 1 ⁄ 3 0 1 ⁄ 3 1 0.5 ⁄ 3 0.5 ⁄ 3 1 ⁄ 3 2 0.5 ⁄ 3 0.5 ⁄ 3 1 ⁄ 3 p(y₃) 2 ⁄ 3 1 ⁄ 3

H(Y) = (2)/(3)log₂(3)/(2) + (1)/(3)log₂3
(x₁, y₃) a b p(x₁) 0 1 ⁄ 3 0 p 1 0.5 ⁄ 3 0.5 ⁄ 3 1 − p 2 0.5 ⁄ 3 0.5 ⁄ 3 0 p(y₃) 1 ⁄ 2 1 ⁄ 2
(x₁, y₃) a b p(x₁) 0 p₀ 0 p₀ 1 0.5⋅p₁ 0.5⋅p₁ p₁ 2 0.5⋅p₂ 0.5⋅p₂ p₂ p(y₃) 1 ⁄ 2 1 ⁄ 2
p₀ + (p₁)/(2) + (p₂)/(2) = (1)/(2)
(p₁)/(2) + (p₂)/(2) = (1)/(2) → p₂ = 1 − p₁
p₀ + p₁ + p₂ = 1 → p₀ + p₁ + 1 − p₁ = 1 → p₀ = 0 → C₁(1, 3) = 0 → uniformna raspredelba na izleznite simboli ne go maksimizira kapacitetot
− H(Y) = p(y₃ = a)⋅log₂(p(y₃ = a)) + p(y₃ = b)⋅log₂(p(y₃ = b))

p(y₃ = a) = p₀ + (p₁)/(2) + (p₂)/(2)

p(y₃ = b) = p₀⋅p(y = b|p₀) + p₁⋅p(y = b|p₁) + p₂⋅p(y = b|p₂) = (p₁)/(2) + (p₂)/(2) p(y₃ = b) = (p₁)/(2) + (p₂)/(2) − H(Y) = ⎛⎝p₀ + (p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝p₀ + (p₁)/(2) + (p₂)/(2)⎞⎠ + ⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠

p₀ = 1 − p₁ − p₂; − H(Y) = ⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ + ⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ = − H(p) H(Y) = H(p) where p = (p₁)/(2) + (p₂)/(2)

Ако ја земам дека униформната распределба ја максимизира ентропијата ќе добијам:

max[H(Y)] = H(p = (1)/(2)) ⇒ (p₁)/(2) + (p₂)/(2) = (1)/(2) ама оваа вредност ќе го направи I(X₁, X₂;Y) = 0

Затоа ќе одам со лагражнови мултипликатори:
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = H(Y) − p(X₁ = 1) − p(X₁ = 2)
I(X₁, X₂;Y) = − ⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ − ⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − p₁ − p₂
f(p_i) = − ⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ − ⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − p₁ − p₂ + λ∑³_i = 1p_i
(∂)/(∂p_i)(f(p_i)) = 0 (∂)/(∂p₁)(f(p_i)) = (1)/(2)⋅log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ − ⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠⋅( − (1)/(2))/(ln(2)⋅ ⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠) − (1)/(2)⋅log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − ⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠⋅((1)/(2))/(ln(2)⋅⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) − 1 + λ = 0

(1)/(2)⋅log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ + (1)/(2⋅ln(2)) − (1)/(2)⋅log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − (1)/(2⋅ln(2)) − 1 + λ = 0 (1)/(2)⋅log₂⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠ − (1)/(2)⋅log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − 1 + λ = 0

(1)/(2)⋅log₂(⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠)/(⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) − 1 + λ = 0 log₂(⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠)/(⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) = 2(1 − λ) (⎛⎝1 − (p₁)/(2) − (p₂)/(2)⎞⎠)/(⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) = 2^{2(1 − λ)} (1)/(⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) − 1 = 2^{2(1 − λ)} (2)/((p₁ + p₂)) − 1 = 2^{2(1 − λ)} ((p₁ + p₂))/(2) = (1)/(1 + 2^{2(1 − λ)})

(p₁ + p₂) = (2)/(1 + 2^{2(1 − λ)}) p₁ = (2)/(1 + 2^{2(1 − λ)}) − p₂ for λ = 0 p₁ = (2)/(5) − p₂; p₁ + p₂ = (2)/(5) ⇒ p₀ = 1 − (2)/(5) = (3)/(5) H(Y) = H((2)/(5)) = 0.9709505947
\mathnormalC₂ = H((2)/(5)) − p₁ − p₂ = H((2)/(5)) − (2)/(5) = 0.5709505947C₁ = (C₂)/(2) = 0.2854752974
Ако земам λ = 1 ⁄ 2:

\strikeout off\uuline off\uwave off(p₁ + p₂) = (2)/(1 + 2^{2(1 − λ)}) = (2)/(3) ⇒ p₀ = (1)/(3)

\strikeout off\uuline off\uwave off\mathnormalC₂ = H((1)/(3))\mathnormal − (2)/(3) = 0.2516291674

Дефинитивно горното решение е подобро!!!!

-Ash проблем 3.7

Ден и пол се обидував да го решам и добијам резултатот \mathchoiceC₁(1, 3) = 0.32C₁(1, 3) = 0.32C₁(1, 3) = 0.32C₁(1, 3) = 0.32. На крај вредноста ја добив откако го видов решението во Textbook-от од Ash. Се работи за користење на резултатот од Теорема 3.3.3 од Ash (има и ваков проблем во Т. Cover EIT) .

⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α 1 − α β 1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦
p₁ = p(x₁); p₂ = p(x₂);
I = H(Y) − H(Y|X); p(y₁) = αp₁ + (1 − α)⋅p₂; p(y₂) = β⋅p₁ + (1 − β)⋅p₂; H(Y) = (αp₁ + (1 − α)⋅p₂)log₂⎛⎝(1)/(αp₁ + (1 − α)⋅p₂)⎞⎠ +

\strikeout off\uuline off\uwave off + (β⋅p₁ + (1 − β)⋅p₂)⋅log⎛⎝(1)/(β⋅p₁ + (1 − β)⋅p₂)⎞⎠

(9) I = − (αp₁ + (1 − α)⋅p₂)log₂(αp₁ + (1 − α)⋅p₂) + (β⋅p₁ + (1 − β)⋅p₂)⋅log(β⋅p₁ + (1 − β)⋅p₂) + p₁(αlog(α) + β⋅log₂β) + p₂((1 − α)log(1 − α) + (1 − β)log₂(1 − β))

Ако α = β = 1 ⁄ 2
I = − 2⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − p₁ − p₂
f(p₁, p₂) = − 2⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − p₁ − p₂ + λ⋅∑²_i = 1p_i
(∂)/(∂p₁)(f(p₁, p₂)) = − 2⋅(1)/(2)⋅log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − 2⋅⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠((1)/(2))/(⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠) − 1 + λ = − log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − 2⋅(1)/(2) − 1 + λ = − log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ − 2 + λ = 0
− log₂⎛⎝(p₁)/(2) + (p₂)/(2)⎞⎠ = 2 − λ log₂(2)/((p₁ + p₂)) = 2 − λ; (2)/((p₁ + p₂)) = 2^2 − λ; (p₁ + p₂) = (2)/(2^2 − λ); p₁ + p₂ = 2^{− 1 + λ}; p₁ + p₂ = 2^{− 1 + λ}; мора λ = 1 но тоа води кон:
I = − log(1)/(2) − 1 = 1 − 1 = 0

Со решавање на 9↑ во Мапле се добива:

(2 α − 1)ln((1 − 2 x)α + x) + (2 β − 1)ln((1 − 2 x)β + x) − (1 − α)ln(1 − α) − (1 − β)ln(1 − β) − β ln(β) + 2 α − 2 + 2 β − α ln(α) = 0
(2 α − 1)ln((1 − 2 x)α + x) + (2 β − 1)ln((1 − 2 x)β + x) − H(α) − H(β) + 2(α + β − 1) = 0
log₂(((1 − 2x)α + x)^{(2α − 1)}((1 − 2 x)β + x)^{(2β − 1)}) = − H(α) − H(β) + 2(α + β − 1)

\strikeout off\uuline off\uwave off(((1 − 2x)α + x)^{(2α − 1)}((1 − 2 x)β + x)^{(2β − 1)}) = 2^{− H(α) − H(β) + 2(α + β − 1)}

2α + 2 αln((1 − 2 x)α + x) + 2β + 2 βln((1 − 2 x)β + x) − ln((1 − 2 x)α + x) − ln((1 − 2 x)β + x) = H(α) + H(β) + 1
Решение од Ash Solutions (ги има во самиот Textbook)

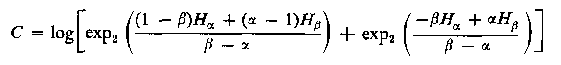
C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦
α = 0 β = 1 ⁄ 2 ⇒

(10) C(0, (1)/(2)) = (ln(5) − 2 ln(2))/(ln(2)) = 0.32

-Во Textbook-от од Ash се користи теоремата T3.3.3

\strikeout off\uuline off\uwave offH(Y|x₂) = H(Y|p₂) = − (p(y₁|x₂)⋅log₂(p(y₁|x₂)) + p(y₂|x₂)⋅log₂(p(y₂|x₂))) = (1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β)

⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α 1 − α β 1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦

Π = ⎡⎢⎣ α 1 − α β 1 − β ⎤⎥⎦ Π^− 1 = (1)/(α − α⋅β − β + α⋅β)⎡⎢⎣ 1 − β α − 1 − β α ⎤⎥⎦ = (1)/(α − β)⎡⎢⎣ 1 − β α − 1 − β α ⎤⎥⎦ = ⎡⎢⎣ (1 − β)/(α − β) (α − 1)/(α − β) − (β)/(α − β) (α)/(α − β) ⎤⎥⎦ = ⎡⎢⎣ q₁₁ q₁₂ q₂₁ q₂₂ ⎤⎥⎦

\strikeout off\uuline off\uwave offC = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦

C = log{∑²_j = 12^{− ∑²_i = 1q_ijH(Y|X = x_i)}} = log{2^{− ∑²_i = 1q_i1H(Y|X = x_i)} + 2^{− ∑²_i = 1q_i2H(Y|X = x_i)}} = log{2^{− q₁₁H(Y|X = x₁) − q₂₁H(Y|X = x₂)} + 2^{− q₁₂H(Y|X = x₁) − q₂₂H(Y|X = x₂)}} =
log{2^{− q₁₁(αlog(α) + β⋅log₂β) − q₂₁((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β))} + 2^{− q₁₂((αlog(α) + β⋅log₂β)) − q₂₂((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β)))}} = log{2^− A + 2^− B}
A: = (1 − β)/(α − β)(αlog(α) + β⋅log₂β) − (β)/(α − β)((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β)) =
((1 − β)(αlog(α) + β⋅log₂β) − β⋅((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β)))/(α − β) =

\strikeout off\uuline off\uwave off(1 − β)(αlog(α) + β⋅log₂β) − β⋅((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β)) = αlog(α) + β⋅log₂β − βαlog(α) − β²⋅log₂β − β(1 − α)log(1 − α) − β(1 − β)⋅log₂(1 − β)

αlog(α) + β⋅log₂β − βαlog(α) − β²⋅log₂β − β(1 − α)log(1 − α) − β(1 − β)⋅log₂(1 − β) = a(1 − b)log(a) − β(1 − α)log(1 − α) + b(1 − b)log(b) − β(1 − β)⋅log₂(1 − β)
(1 − β)(αlog(α) + β⋅log₂β) − β⋅((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β))
B = (α − 1)/(α − β)((αlog(α) + β⋅log₂β)) + (α)/(α − β)((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β))) =
(α − 1)(αlog(α) + β⋅log₂β) + α((1 − α)log(1 − α) + (1 − β)⋅log₂(1 − β))) = (α − 1)αlog(α) + (α − 1)β⋅log₂β + α(1 − α)log(1 − α) + α(1 − β)⋅log₂(1 − β))
(α − 1)αlog(α) + (α − 1)β⋅log₂β + α(1 − α)log(1 − α) + α(1 − β)⋅log₂(1 − β))
-Гомнар сум дефиницијата на каналната матрица е како во Теорија на информации!!!!!!!!!!!!!!
P_y = ⎡⎢⎢⎢⎣ p(Y₁) p(Y₂) p(Y₃) ⎤⎥⎥⎥⎦; Π = ⎡⎢⎢⎢⎣ p₁₁ p₁₂ p₁₃ p₂₁ p₂₂ p₂₃ p₃₁ p₃₂ p₃₃ ⎤⎥⎥⎥⎦; P_x = ⎡⎢⎢⎢⎣ p(X₁) p(X₂) p(X₃) ⎤⎥⎥⎥⎦; P_y = Π^TP_x; ⎡⎢⎢⎢⎣ p(Y₁) p(Y₂) p(Y₃) ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ p₁₁ p₂₁ p₃₁ p₁₂ p₂₂ p₃₂ p₁₃ p₂₃ p₃₃ ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(X₁) p(X₂) p(X₃) ⎤⎥⎥⎥⎦

-Одам повторно со дефиницијата на канална матрица како во Теорија на информации

\mathchoice⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α1 − α β1 − β ⎤⎥⎦^T⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ αβ 1 − α1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ p(y₁|x₁)p(y₁|x₂) p(y₂|x₁)p(y₂|x₂) ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α1 − α β1 − β ⎤⎥⎦^T⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ αβ 1 − α1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ p(y₁|x₁)p(y₁|x₂) p(y₂|x₁)p(y₂|x₂) ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α1 − α β1 − β ⎤⎥⎦^T⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ αβ 1 − α1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ p(y₁|x₁)p(y₁|x₂) p(y₂|x₁)p(y₂|x₂) ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦⎡⎢⎣ p(y₁) p(y₂) ⎤⎥⎦ = ⎡⎢⎣ α1 − α β1 − β ⎤⎥⎦^T⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ αβ 1 − α1 − β ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦ = ⎡⎢⎣ p(y₁|x₁)p(y₁|x₂) p(y₂|x₁)p(y₂|x₂) ⎤⎥⎦⎡⎢⎣ p(x₁) p(x₂) ⎤⎥⎦
Π = (1)/(α − α⋅β − β + α⋅β)⎡⎢⎣ 1 − β α − 1 − β α ⎤⎥⎦ = (1)/(α − β)⎡⎢⎣ 1 − β α − 1 − β α ⎤⎥⎦ = ⎡⎢⎣ (1 − β)/(α − β) (α − 1)/(α − β) − (β)/(α − β) (α)/(α − β) ⎤⎥⎦ = ⎡⎢⎣ q₁₁ q₂₁ q₁₂ q₂₂ ⎤⎥⎦
Види ги индексите на q. Намерно ги ставив така за да излезе резултатот како во книгата на Ash. Нема врска треба да бидат: ⎡⎢⎣ q₁₁ q₁₂ q₂₁ q₂₂ ⎤⎥⎦
Мислам дека сум го помешал j со i во формулата 3.3.5 од Ash.
H(Y|x₁) = H(Y|p₁) = − (p(y₁|x₁)⋅log₂(p(y₁|x₁)) + p(y₂|x₁)⋅log₂(p(y₂|x₁))) = − αlog(α) − (1 − α)⋅log₂(1 − α) = H(α)

\strikeout off\uuline off\uwave offH(Y|x₂) = H(Y|p₂) = − (p(y₁|x₂)⋅log₂(p(y₁|x₂)) + p(y₂|x₂)⋅log₂(p(y₂|x₂))) = − β⋅log(β) − (1 − β)⋅log₂(1 − β) = H(β)

\strikeout off\uuline off\uwave offlog{2^{− q₁₁H(α) − q₂₁H(β)} + 2^{− q₁₂H(α) − q₂₂H(β)}} = log{2^{− (1 − β)/(α − β)⋅H(α) − (a − 1)/(α − β)⋅H(β)} + 2^{+ (β)/(α − β)⋅H(α) − (α)/(α − β)⋅H(β)}} = log{2^{(1 − β)/(β − α)⋅H(α) + (a − 1)/(β − α)⋅H(β)} + 2^{− (β)/(β − α)⋅H(α) + (α)/(β − α)⋅H(β)}} = log{2^{((1 − β)H(α) + (a − 1)H(β))/(β − α)} + 2^{( − β⋅H(α) + αH(β))/(β − α)}}

\mathchoiceC = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦ Ова е уште поопшта форма од онаа во Cover 2^C = 2^C₁ + 2^C₂
α = 0 β = 1 ⁄ 2 ⇒
Π = ⎡⎢⎣ α 1 − α β 1 − β ⎤⎥⎦ = ⎡⎢⎣ 0 1 0.5 0.5 ⎤⎥⎦
C = log₂⎡⎣exp₂⎛⎝( − H_β)/(0.5)⎞⎠ + exp₂⎛⎝(0)/(β − α)⎞⎠⎤⎦ = log₂[exp₂( − 2) + 1] = log₂⎡⎣(1)/(4) + 1⎤⎦ = log₂⎡⎣(5)/(4)⎤⎦ = log₂(5) − 2⋅log₂(2) = 0.32
\mathchoiceC(0, (1)/(2)) = (ln(5) − 2 ln(2))/(ln(2)) = 0.32C(0, (1)/(2)) = (ln(5) − 2 ln(2))/(ln(2)) = 0.32C(0, (1)/(2)) = (ln(5) − 2 ln(2))/(ln(2)) = 0.32C(0, (1)/(2)) = (ln(5) − 2 ln(2))/(ln(2)) = 0.32
-Сегам сакам да проверам дали истото важи и за за 3x2 матрицата од чланакот
y₃|x₁ a b 0 1 0 1 0.5 0.5 2 0.5 0.5
Нема шанси. Aко матрицата не е квадратна не можеш да пресметаш инверзна матрица.

-Продолжувам со чланакот на страна 127. Да видам каква е каналната матрица ако x₂ = 0

(11) y₃|x₁ a b 0 1 ⁄ 2 1 ⁄ 2 1 1 ⁄ 2 1 ⁄ 2 2 1 ⁄ 2 1 ⁄ 2

In both cases the channel matrix has a capacity equal to 0.32 ([1], page 85, problem 3.7). If x₂ is held to zero, all input letters x₁ appear completely noisy at terminal 3. Ова е логично и следи директно од 11↑. (За било кој влезен симбол y₃ подеднакво е веројатно да биде а т.е b. Со тоа неговата вредност е целосно неизвесна знаејќи ги влезните симболи. Затоа вели дека сите влезни симболи x₁ се појавуваат целосно ошумени во терминалот 3). Thus C₁(1, 3) = 0.32. (Мене ова не ми изгледа логично да важи за кејсот x₂ = 0 . Ваква вредност се добиваат само ако за еден влезен симбол еден излезен е со веројатност 1, а за другиот влезен изезот е пата-пата. Види го решението 10↑). Ова што го користат согласно проблемот 3.7 од Ash ми изгледа сосема логично. Имено користат само два кодни знака за кодирање на кодните зборови т.е W ∈ {1, ..M} = {1, ..2^nR} = {1, ...2^1⋅1} = {1, 2}. Ако користиш три кодни знака ќе треба добиениот капацитет да го делиш со log₂(M).

-Да видам што се добива ако во 1↑ земам x₂ = 1 i.e x₂ = 2 :

y₃|x₁ a b 0 1 0 1 1 ⁄ 2 1 ⁄ 2 2 1 ⁄ 2 1 ⁄ 2 y₃|x₁ a b 0 0 1 1 1 ⁄ 2 1 ⁄ 2 2 1 ⁄ 2 1 ⁄ 2

In other words, if terminal 2 keeps his input x₂ fixed at 1 or 2 there exist a code for sending in the 1-3 direction at rate arbitrarily close to 0.32. (Ова би рекол дека е точно само ако се пренесуваат симболите 0 и 1 или 0 и 2. Aко одиш со три симболи немаш квадратна матрица и нема да можеш да ја користиш Theorem 3.3.3 од Ash која користи инверзна канална матрица за пресметка на капацитетот.)

Figure 5 Three-terminal detailed

There is still another way of transmitting information over the channel which enables terminal 1 to send to terminal 3 at a rate up to 0.5. This may be seen as follows. If x₂ is held at zero it is possible to transmit in the 1-2 direction at rate one. In that case the letters 1 and 2 transmitted at terminal 1 result with certainty in a an b respectively at terminal 2.

-Да го добијам ова со користење на Табела I:
y₂|x₁ a b 0 1 ⁄ 2 1 ⁄ 2 1 1 0 2 0 1
Апсолутно е точно тврдењето во црвено!!!
29.06.2014
во табелата горе е дадена условна веројатност!!!!
H(Y₂|X₁) = p(X₁ = 1)H(Y₂|X₁ = 1) + p(X₁ = 2)H(Y₂|X₁ = 2) = 0
I(X₁;Y₂) = H(Y₂) − 0 = H⎛⎝(1)/(2)⎞⎠ = 1
пази!!! 0-та пошто е целсно ошумена не ја земам во предвид при пресметка на H(Y₂).

Otherwise if we held x₂ at 1 or 2 the x₁ letters appear completely noisy at terminal 2.

y₂|x₁ a b 0 1 ⁄ 2 1 ⁄ 2 1 1 ⁄ 2 1 ⁄ 2 2 1 ⁄ 2 1 ⁄ 2 y₂|x₁ a b 0 1 ⁄ 2 1 ⁄ 2 1 1 ⁄ 2 1 ⁄ 2 2 1 ⁄ 2 1 ⁄ 2

Similarly if x₁ is held at zero it is possible to send one bit per second in the 2-3 direction by using only the letters 1 and 2 at terminal 2 which then result with certainty in a and b respectively at terminal 3.

y₃|x₂ a b 0 1 ⁄ 2 1 ⁄ 2 1 1 0 2 0 1

Otherwise all x₂ letters appear completely noisy at terminal 3. It is therefore possible to send one bit per second in both directions, however not simultaneously.

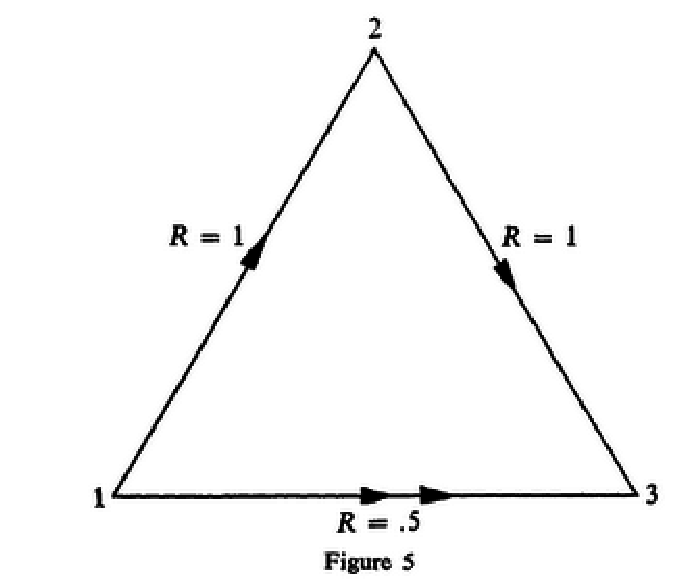
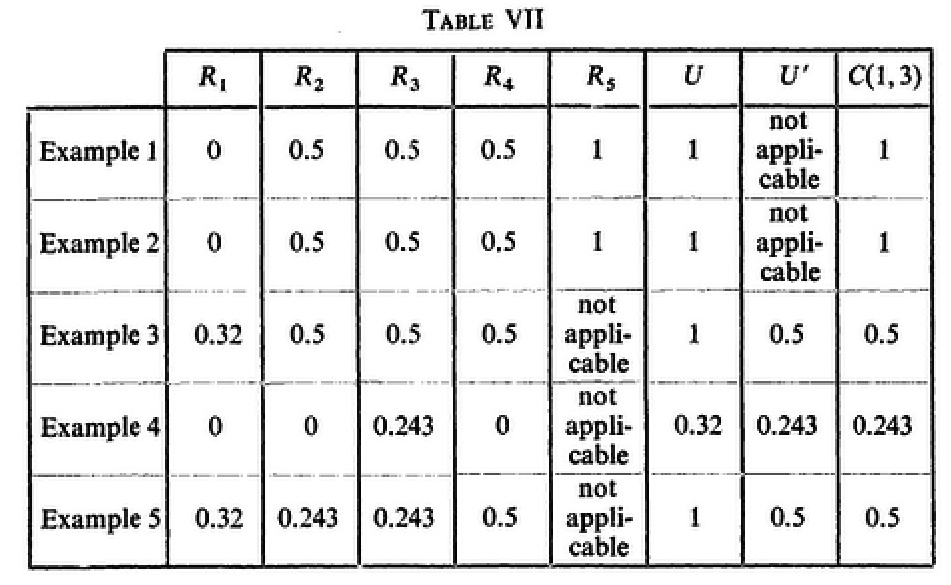
Let now, the three teminals adopt the following strategy. First x₂is held at 0 and terminal 1 sends information to terminal 2 at rate one. Then x₁ is held at 0 and terminal 2 sends the received information on to terminal 3, also at rate one. By dividing the time for use of these two strategies in the ratio λ to 1 − λ , it is possible to transmit in the 1-3 direction at a rate equal to the smallest of the two numbers λ and 1 − λ, that is, at a rate up to 0.5. We summarize the rezult in 6↓. It will follow from later results that it is not possible to transmit in 1-3 direction at rate higher than 0.5 with arbitrary small proability of error.

Figure 6 Sumarized

Example 4

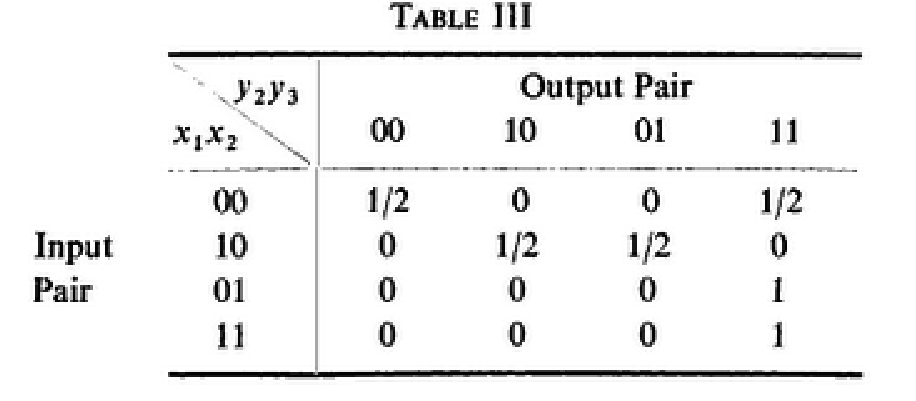
In the previous examples we have seen how terminal 1 can achieve a transmission rate different from C₁(1, 3) by first sending information to terminal 2 who then sends the received information on to terminal 3. Suppose now that both C₁(1, 2) and C₁(1, 3) are equal to zero. In this case terminal 1 cannot influence either the otuputs at terminal 2 or the outputs at terminal 3 in one single channel operation, and the two different methods indicated in example 3 for sending in the 1-3 direction both fail. As we shall see there may still exist a method to send information at a positive rate from terminal 1 to terminal 3. Suppose all input and output letters in this example are binary. Let the probabilities P(y₂, y₃|x₁, x₂|x₃) of different output pairs (y₂, y₃) conditional on various input pairs (x₁, x₂), for arbitrary x₃ , be given in 3↓.

Table 3 Example 4

No matter which letter terminal 2 transmits (either 0 or 1) all input letters x₁ appear completely noisy at both terminal 2 and terminal 3. Thus \mathchoiceC₁(1, 2) = C₁(1, 3) = 0C₁(1, 2) = C₁(1, 3) = 0C₁(1, 2) = C₁(1, 3) = 0C₁(1, 2) = C₁(1, 3) = 0.

One might expect that no communication is possible from terminal 1 to terminal 3 at all. Surprisingly enough, however, it will turn out that one can transmit over this channel in the 1-3 direction at rate of 0.24.

Suppose x₂ is held at zero. The conditional probabilities P(y₂, y₃|x₁|x₂) as x₂ = 0 are given by the first two rows of 3↑. Together these two rows form a loss-less channel for sending from terminal 1 to pair of terminals (2, 3). That is C₁[1, (2, 3)] = 1. If the receiver at terminal 3 could see both outputs y₂ and y₃ received over this loss-less channel he would be able to specify the transmitted x₁ uniquely.

If the observed y₂ and y₃ are the same, he knows x₁ = 0 was sent. If y₂ and y₃ are different he knows x₁ = 1 was sent. Terminal 3 could learn about the output letter y₂ if terminal 2 sends information about this letter over the channel after he has observed it himself. If x₁ = 0 the corresponding channel p(y₃|x₂|x₁) for sending from terminal 2 to terminal 3 has capacity equal to 0.32. This method clearly provides a rule for the three terminal for sending in two channel operations information from terminal 1 to terminal 3. By deviding the time for use of these two strategies in the right proportion it is possible to transmit in the 1-3 direction at rate up to:

\mathchoiceC = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424 Не знам од каде доаѓа ова!!!(изгледа од формулите во глава 7)

Изгледа ова е согласно 44↓.

\strikeout off\uuline off\uwave offR₃ = (C₁[1, (2, 3)]⋅C₁(2, 3))/(C₁(2, 3) + logb₂)

Figure 7 Example 4 figure

Schematically we have represented these results in 6↑.

Example 5

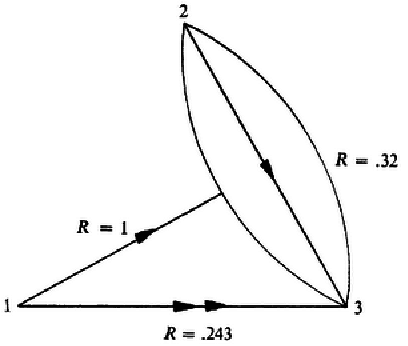
Here is another simple example which shows yet another way of sending information from terminal 1 to terminal 3. The method to be describet here is better, for this particular channel, than any of the methods described in the foregoing examples. Suppose for this channl all inputs and output letters are again binary. Let the probabilities P(y₂, y₃|x₁, x₂|x₃) of different output pairs (x₁, x₂) be the same for different x₃ and be given by 4↓.

Table 4 Table IV

Let us first compare for this example the various methods of transmission described in the previous examples. It is not hard to see that for this example C₁(1, 3) = C₁(2, 3) = 0, 32 (логично е зошто и во давата случаи ако го држиш другиот симбол фиксен y₃ е фиксиран за едната излезна вредност за еден влезен симбол со веројатнос 1, а за другиот со пата-пата веројатност меѓу двете излезни вредности). We observe that, regardless of which letter terminal 2 puts in, the letters 0 and 1 transmitted at terminal 1 result with certainty into 0 and 1 respectively at terminal 2. Therefore C₁(1, 2) = 1 and also C₁[1, (2, 3)] = 1 (Второво важи за било која вредност на x₂). Thus if terminal 1 first sends information at rate one to terminal 2, who then sends the received information on to terminal 3 at rate 0.32, transmission in the 1-3 direction is possible at rate equal to:

\mathchoiceC = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424C = (0.32)/(1 + 0.32) = 0.242424

Similarly if terminal 1 sends information to the pair of terminals (2,3) at rate one, and terminal 2 sens information about the received letter sequence to terminal 3 at rate o.32, it is posible to transmit in 1-3 direction at rate 0.243. Thus, using any of the methods described so far, the highest rate taht can be attained is 0.32.

We now propose a forth method which in this particular example will enable terminal 1 to transmit to terminal 3 at a rate arbitrarily close to \mathchoice0.50.50.50.5.

The conditional probabilities P(y₃|x₁, x₂) are given by

y₃|x₁, x₂ 0 1 00 1 0 10 1 ⁄ 2 1 ⁄ 2 01 1 ⁄ 2 1 ⁄ 2 11 0 1

The capacity of this channel matrix is clearly equal to one and is achieved by using only the input pairs (0, 0) and (1,1). Thus \mathchoiceC₁[(1, 2)3] = 1C₁[(1, 2)3] = 1C₁[(1, 2)3] = 1C₁[(1, 2)3] = 1.

Suppose a person could operate the inputs at both terminal 1 and 2 simultaneously. In sending to terminal 3 he would make use only of the input pairs (0,0) and (1,1). These pairs are received as 0 and 1 respectively at terminal 3. Now terminal 1 can in fact control the inputs at terminal 1 and 2 as follows.

He may first send a letter to terminal 2 over the noiseless channel P(y₂|x₁|x₂) instructing terminal 2 which letter to send durin the next period. (каналот x₁ → y₂ e безшумен зошто ако пратиш x₁ = 0 (без оглед на x₂) со сигруност добиваш y₂ = 0 и обратно ако пратиш x₁ = 1 (без оглед на x₂) со сигруност добиваш y₂ = 1). At the next input terminal 2 sends the letter terminal 1 has instructed him to send, and terminal 1 himself also puts in a letter to the channel. This pair together is then transmitted to terminal 3. In the decoding procedure terminla 3 only pays attention on the second letter received. In this particular example suppose terminal 1 wants to send a 0 to terminal 3. He then first puts in a 0 which is received as 0 at terminal 2. At the next period both terminal 1 and terminal 2 put in a 0, which pair is then received with certainty as 0 at termina 3 and decoded correctly there as 0. By deviding the time for use of these two strategies into equal periods it is possible here to transmit in the 1-3 direction at a rate equal to 0.5 Претпоставувам дека се добива од (1)/(1 + 1) = 0.5 . Thus the forth method yields a result which, for this particular example, is better than the rates provided by the previous methods. The result is summarized in 8↓.

Figure 8 Forth Method

It is shown in Section 10 that it is not possible to transmit in the 1-3 direction at rate higher than 0.5 with arbitrarily small probability of error.

4 Basic inequality for single-letter capacities

In Section 2 we introduced the capacities C₁(1, 2), C₁(1, 3), C₁(2, 3), C₁[1, (2, 3)] and C₁[(1, 2), 3] in order to illustrate the different ways of transmission through the channel. In this section we give precise definitions of these capacities. They are called single-letter capacities since they correspond to one single channel operation and involve a maximizing process over single input letters to the channel only. The single-letter capacities satisfy a number of inequalities similar to the properties of average mutual inforamtion functions which are standard in information theory.

Let a d.m three terminal channel P(y₁y₂y₃|x₁x₂x₃) be given. For fixed inputs x₂ and x₃ and a probability distribution P(x₁) on input x₁ there is a corresponding probability distribution on the set A₁x B₂x B₃ of triples (x₁, y₂, y₃) defined by:

(12) P(x₁, y₂, y₃|x₂x₃) = ⎲⎳_y₁P(y₁, y₂, y₃|x₁, x₂, x₃).P(x₁)

Let

(13) 1R[1, (2, 3)|P(x₁);x₂, x₃] = E⎡⎣log⎛⎝(P(x₁, y₂, y₃|x₂, x₃))/(P(x₁)P(y₂, y₃|x₂x₃))⎞⎠⎤⎦

Логично е вака што го пишува на левата страна зата што во генерален случај треба во именителот да иамаш P(x₁|x₂x₃) но x₁ не зависи од x₂ и x₃ па затоа имаш само P(x₁) .

where the expected value is taken with respect to the distribution 12↑.

I(X;Y) = H(Y) − H(Y|X); I(X;Y) = ⎲⎳_x, yp(x, y)⋅log₂⎛⎝(p(x, y))/(p(x)⋅p(y))⎞⎠ = ⎲⎳_x, yp(x, y)⋅log₂⎛⎝(1)/(p(x))⎞⎠ + ⎲⎳_x, yp(x, y)⋅log₂⎛⎝(p(x, y))/(p(y))⎞⎠

⎲⎳_x, yp(x, y)⋅log₂⎛⎝(1)/(p(x))⎞⎠ + ⎲⎳_x, yp(x, y)⋅log₂⎛⎝(p(x, y))/(p(y))⎞⎠ = ⎲⎳_xp(x)⋅log₂⎛⎝(1)/(p(x))⎞⎠ + ⎲⎳_x, yp(x, y)⋅log₂(p(x|y))

= ⎲⎳_x, yp(x, y)⋅log₂⎛⎝(1)/(p(x))⎞⎠ − ⎲⎳_x, yp(x, y)⋅log₂(1)/((p(x|y))) = H(x) − H(X|Y)

(Значи P(y₂, y₃|x₂x₃) одговара на p(y) од подвлечениот дел од изразот погоре.)

R(1, (2, 3)|P(x₁);x₂, x₃) = I(X₁;Y₂Y₃|x₂x₃)

(Ги пишувам x₂x₃ со мали букви зошто не одам по сите нивни вредности туку за една нивна фиксна вредност. Означувањето што го користат во чланаков мислам дека е слично. Со малите вредности на x2 и x3 сака да каже дека се фиксни вредности, а со P(x1) сака да каже дека се работи за сите вредности на x1).

We may write 13↑ also as:

(Тука мојот резон се изедначува со оној во чланакот).

That is uncertainty of x₁ , less the uncertainty in x₁ given y₂ and y₃ on the average, with respect to P(x₁, y₂, y₃|x₂x₃). Define

C₁[1, (2, 3)] = max_x₂, x₃max_p(x₁)[1, (2, 3)|P(x₁);x₂x₃]

Овде мислам деака сака да каже дека го пресметува вториот max за различни вредности на (x₂, x₃) и потоа пара супремум од добиените максимуми.

Similarly let:

(15) R[1, 2|P(x₁);x₂x₃] = H(X₁) − H(X₁|Y₂, x₂x₃) = E⎡⎣log⎛⎝(P(x₁, y₂|x₂, x₃))/(P(x₁)P(y₂|x₂x₃))⎞⎠⎤⎦

and

R[1, 3|P(x₁);x₂x₃] = H(X₁) − H(X₁|Y₃, x₂x₃) = E⎡⎣log⎛⎝(P(x₁, y₃|x₂, x₃))/(P(x₁)P(y₃|x₂x₃))⎞⎠⎤⎦

where both expectations are taken with respect to distribution12↑. Define

C₁[1, 2] = max_x₂, x₃max_p(x₁)R[1, 2|P(x₁);x₂x₃]

C₁[1, 3] = max_x₂, x₃max_p(x₁)R[1, 3|P(x₁);x₂x₃]

Now let the inputs x₁, x₃ be fixed and suppose a probability distribution P(x₂) is given on inputs x₂. Then

(16) P(x₂, y₃|x₁x₃) = ⎲⎳_y₁, y₂P(y₁, y₂, y₃|x₁, x₂, x₃).P(x₂)

determines a probability distribution on pairs (x₂, y₃). Let

(17) R[2, 3|P(x₂);x₁x₃] = H(X₂) − H(X₂|Y₃, x₂x₃) = E⎡⎣log⎛⎝(P(x₂, y₃|x₁, x₃))/(P(x₂)P(y₃|x₁x₃))⎞⎠⎤⎦

where the expected value is taken with respect to the distribution 16↑. Define

(18) C₁[2, 3] = max_x₁, x₃max_p(x₂)R[2, 3|P(x₂);x₁x₃]

Finaly let the input x₃ be fixed and suppose P(x₁, x₂) is given probability distributon on pairs of inputs (x₁, x₂). Then

(19) P(x₁x₂, y₃|x₃) = ⎲⎳_y₁y₂P(y₁, y₂, y₃|x₁x₂, x₃)⋅P(x₁x₂)

determines a probability distribution on triples (x₁, x₂, x₃). Let

where expected value is taken with respect to 19↑. Define:

C₁[(1, 2), 3] = max_x₃max_{P(x₁, x₂)}R[(1, 2), 3|P(x₁x₂); x₃]

We now state and prove a number of inequalities satisfied by the various single-letter capacities just defined. These inequalities are basic to understand the underlying ideas and are being used throughout.

Lema 4.1

C₁(1, 3) ≤ C₁[1, (2, 3)] with equality if both

P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁, x₂, x₃)P(y₃|x₁, x₂, x₃)

(i.e., the outputs y₂ and y₃ are conditionaly independent given the inputs x₁x₂ and x₃), and \mathchoiceC₁(1, 2) = 0C₁(1, 2) = 0C₁(1, 2) = 0C₁(1, 2) = 0.

Дискусија

(Маливе букви значат фиксни вредности а не случајни променливи па затоа не ги земам во предвид во chain rule.)

= I(X₁;Y₃) = \mathchoiceC₁[1, 3]C₁[1, 3]C₁[1, 3]C₁[1, 3]

Lema 4.2

C₁(1, 2) ≤ C₁[1, (2, 3)] with equality if both

P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁, x₂, x₃)⋅P(y₃|x₁x₂x₃)

and C₁(1, 3) = 0

Proof:

C₁(1, 3) = 0 ⇒ I(X₁;Y₃) = H(X₁) − H(X₁|Y₃) = 0 ⇒ H(X₁|Y₃) = H(X₁) ⇒ X₁ andY₃ are independendt.

\overset(a) = H(Y₂|Y₃) − H(Y₂|X₁, Y₃ x₂, x₃) = I(X₁;Y₂|Y₃) = H(X₁|Y₃) − H(X₁|Y₂Y₃) = H(X₁) − H(X₁|Y₂) = \mathchoiceI(X₁;Y₂)I(X₁;Y₂)I(X₁;Y₂)I(X₁;Y₂)

(a)-since Y₂ and Y₃ are independent given X₁, x₂, x₃

Corollary 4.1

\strikeout off\uuline off\uwave offIf C₁[1, (2, 3)] = 0 then C₁(1, 2) = C₁(1, 3) = 0

Lemma 4.3

C₁(1, 3) ≤ C₁[(1, 2), 3] with equality \mathchoiceC₁(2, 3) = 0C₁(2, 3) = 0C₁(2, 3) = 0C₁(2, 3) = 0

Proof:

C₁(2, 3) = 0 ⇒ X₂ and Y₃ are independent. of

Овде претпоставувам дека:

P(x₁, x₂|y₃x₃) = P(x₁|y₃, x₃)⋅P(x₂|Y₃, x₃)

= \cancelH(X₂) + H(X₁|X₂) − H(X₁|Y₃, x₂, x₃) − \cancelH(Y₂) = H(X₁|X₂) − H(X₁|X₂, Y₃, x₂, x₃) = I(X₁;Y₃|X₂) = H(Y₃|X₂) − H(Y₃|X₁X₂) =

\strikeout off\uuline off\uwave off = H(Y₃) − H(Y₃|X₁) = \mathchoiceI(X₁;Y₃)I(X₁;Y₃)I(X₁;Y₃)I(X₁;Y₃)

(a)-since X₁ and X₂ are independent given Y₃

Lemma 4.4

C₁(2, 3) ≤ C₁[(1, 2), 3] with equality \mathchoiceC₁(1, 3) = 0C₁(1, 3) = 0C₁(1, 3) = 0C₁(1, 3) = 0

Corollary 4.2

C₁[(1, 2), 3] = 0 if and only if C₁(1, 3) = C₁(2, 3) = 0

Table 5 Tbl VI

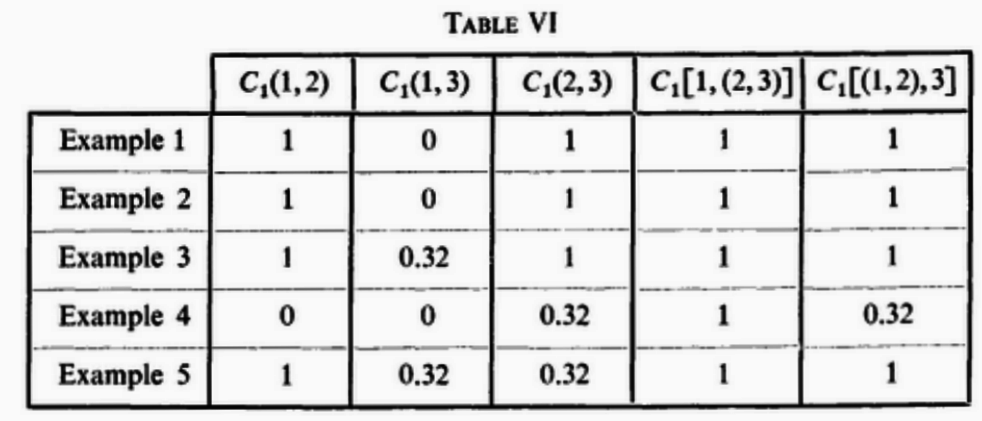
Remark. In 5↑ we have evaluated for each example of Section 3 the single-letter capacities C₁(1, 2), C₁(1, 3), C₁(2, 3), C₁(1, (2, 3)) and C₁[(1, 2), 3].

In Example 4 one has C₁(1, 2) = C₁(1, 3) = 0 (ова на прв поглед важи само за x₂ = 0 но подолу го изведов и за x₂ = 1) but C₁[1, (2, 3)] = 1. Thus the converse of corollary 4.1 is not necessarily true. The converse holds only if:

P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁, x₂, x₃)⋅P(y₃|x₁x₂x₃)

Да, затоа што во тој случај Лемата 4.2 е со еднаквост т.е. 0 = C₁(1, 2) = C₁[1, (2, 3)]

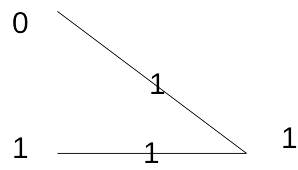
max_p(x)I(X;Y) = H(X) − H(X|Y) = log₂(2) − 1\overset(a) = 0 I(X;Y) = H(Y) − H(Y|X)\overset(b) = 1log(1) − 0
(a) Кога ќе го примиш Y имаш максимална неизвесност. Можеби е пратена 0 а можеби 1.
(b) Не посоти неизвесност. Ако пратиш x = 0 → y = 1, ако праитиш x = 1 пак y = 1.

it clearly sufices to prove only Lemmas 4.1 and 4.3

Proof of Lemma 4.1

Let x₂ and x₃ be fixed and let P(x₁) be a given probability distribution on inputs x₁. It follows form Feinstein ([3], page 16, Lemma 6) that

R(1, 3|P(x₁);x₂, x₃) ≤ R[1, (2, 3)|P(x₁);x₂, x₃]

I(X₁;Y₃|X₁) = ?

Чудна работе е што вториот член ми изгледа дека треба да биде 0 без никакви предуслови. H(X1|X1)=0!?

- Now assume P(y₂, y₃|x₁, x₂, x₃) = P(y₂|x₁, x₂, x₃)⋅P(y₃|x₁x₂x₃) for all x₁, x₂, x₃, y₂ and y₃ and suppose C₁(1, 2) = 0. The last assumption means that for all x₂, x₃, y₂ fixed P(y₂|x₁x₂x₃) remains the same as x₁ varies (Ова е логично зошто y₂ не зависи од x₁ заради C₁(1, 2) = 0. Јас би рекол дека уште и дека) ([7] page 17). Thus

for all y₂, y₃ and x₁.

It follows that

(21) P(y₂, y₃|x₁, x₂, x₃)⋅P(y₃|x₂, x₃) = P(y₂, y₃|x₂, x₃)⋅P(y₃|x₁, x₂, x₃)

Иницијален обид за да го докажам како се доаѓа до 22↓

Proof

Уште еден обид

or alternatively

(22) P(x₁, y₂|y₃, x₂, x₃) = P(x₁|y₃x₂x₃)⋅P(y₂|y₃, x₂, x₃)

Од 21↑ следи дека:

\strikeout off\uuline off\uwave offP(y₂, y₃|x₁, x₂, x₃)⋅P(y₃|x₂, x₃) = P(y₂, y₃|x₂, x₃)⋅P(y₃|x₁, x₂, x₃)

Во изразот 22↑не гледам ништо спорно

(b) - y₂ и x₁ се статистички независни зошто C₁(1, 2) = 0. (Да ама тоа изгледа не е доволен услов).

that is x₁ and y₂ are conditionally independent given y₃; for each x₂ and x₃ fixed (⊛). (Ова е суштинска констатација ама нешто матно ми изглеа како се стига до неа)

In terms of conditional uncertainties this means H(X₁|Y₃, x₂, x₃) = H(X₁|Y₂, Y₃, x₂, x₃) (ова е јасно ако се земе во предвид ⊛) , therefore

R(1, 3|P(x₁);x₂, x₃) = R[1, (2, 3)|P(x₁);x₂, x₃)]

for all x₂, x₃ and P(x₁). Hence C₁(1, 3) = C₁[1, (2, 3)]. This completes the proof.

Proof of Lemma 4.3. Let x₃ be fixed and let a probability distribution P(x₁, x₂) on pairs of inputs x₁ and x₂ be given.

Let

I(X₁;Y₃|X₂, x₃) = H(Y₃|X₂, x₃) − H(Y₃|X₁, X₂, x₃) =

= E⎡⎣log₂⎛⎝(p(y₃| x₁, x₂, x₃))/(p(y₃| x₂, x₃))⎞⎠⎤⎦

where the expected value is taken with respect to the distribution 19↑. Clearly

(a) ова е мое толкување за мапирање меѓу номенклатурата во T. Cover и Van. der Moulen.

It is easily verified that

max_x₂max_P(x₁)R(1, 3|P(x₁);x₂, x₃) = max_P(x₁x₂){H(Y₃|X₂, x₃) − H(Y₃|X₁, X₂, x₃)}

Hence: C₁(1, 3) ≤ C₁[(1, 2), 3]

Now suppose C₁(2, 3) = 0. This implies that for all x₁, x₃, y₃ fixed \strikeout off\uuline off\uwave offP(y₃|x₁, x₂, x₃) stays same as as x₂ varies\uuline default\uwave default. Or, if x₃ is fixed, the matrix of conditional probabilities P(y₃|x₁|x₂, x₃) is the same for different x₂.

C₁(1, 3|x₂x₃) = max_P(x₁)[R(1, 3|P(x₁);x₂x₃)]

\strikeout off\uuline off\uwave off

R(1, 3|P(x₁), x₂, x₃) = H(Y₃) − H(Y₃|X₁|x₂x₃) = I(X₁;Y₃) = H(Y₃) − H(Y₃|X₁) =

= − ⎲⎳_y₃p(y₃) log₂(p(y₃)) − ⎲⎳_x₁y₃p(x₁)p(y₃|x₁|x₂x₃) log₂(p(y₃|x₁|x₂x₃)

\strikeout off\uuline off\uwave offC₁(1, 3|x₂, x₃) denotes the capacity of channel P(y₃|x₁|x₂, x₃) for x₂ and x₃ fixed. \uuline default\uwave defaultThus C₁(1, 3|x₂, x₃) is the same for different x₂. Consider now the channel formed by the conditional probabilities P(y₃|x₁, x₂|x₃) as x₃ is fized and x₁ and x₂ vary. This matrix can be partitioned into identical subchannels P(y₃|x₁|x₂x₃) one coresponding to each valuex₂. C₁[(1, 2), 3|x₃] = max_{P(x₁, x₂)}R((1, 2), 3|P(x₁, x₂);x₃) denotes the capacity of channel P(y₃|x₁, x₂|x₃), x₃ fixed. Because of the decomposition of the channel into identical matrices, the capacity C₁[(1, 2), 3|x₃] can be achieved by using a probability distribution P(x₁, x₂) which assigns probability one to an arbitrary but fixed value of x₂ only. But then C₁[(1, 2), 3|x₃] = C₁(1, 3|x₂, x₃) for all x₂. Now maximizing with respct to x₃ we obtain \strikeout off\uuline off\uwave offC₁[(1, 2), 3] = C₁(1, 3) which completes the proof of the lemma.

5 Definitions (encoding functions)

An encoding system of word length n ≥ 1 for transmitting M ≥ 1 messages from terminal 1 to terminal 3 over a d.m. three-terminal channel P(y₁, y₂, y₃|x₁, x₂, x₃) consist of:

(i) M encoding functions F₁(m), m = 1, ..., M, at terminal 1

\mathchoiceF₁(m) = {f⁰₁(m), f¹₁(m, y₁₁), ..., f^n − 1₁(m, y₁₁, ..., y_{1, n − 1})}F₁(m) = {f⁰₁(m), f¹₁(m, y₁₁), ..., f^n − 1₁(m, y₁₁, ..., y_{1, n − 1})}F₁(m) = {f⁰₁(m), f¹₁(m, y₁₁), ..., f^n − 1₁(m, y₁₁, ..., y_{1, n − 1})}F₁(m) = {f⁰₁(m), f¹₁(m, y₁₁), ..., f^n − 1₁(m, y₁₁, ..., y_{1, n − 1})}

(ii) one strategy F₂ at terminal 2

\strikeout off\uuline off\uwave off\mathchoiceF₂(m) = {x₂₁, f¹₂(x₂₁, y₂₁), ..., f^n − 1₂(x₂₁, .., x_{2, n − 1};y₂₁, ..., y_{2, n − 1})}F₂(m) = {x₂₁, f¹₂(x₂₁, y₂₁), ..., f^n − 1₂(x₂₁, .., x_{2, n − 1};y₂₁, ..., y_{2, n − 1})}F₂(m) = {x₂₁, f¹₂(x₂₁, y₂₁), ..., f^n − 1₂(x₂₁, .., x_{2, n − 1};y₂₁, ..., y_{2, n − 1})}F₂(m) = {x₂₁, f¹₂(x₂₁, y₂₁), ..., f^n − 1₂(x₂₁, .., x_{2, n − 1};y₂₁, ..., y_{2, n − 1})}

(iii) one strategy F₃ at terminal 3

\strikeout off\uuline off\uwave off\mathchoiceF₃(m) = {x₃₁, f¹₃(x₃₁, y₃₁), ..., f^n − 1₃(x₃₁, ..., x_{3, n − 1};y₃₁, ..., y_{3, n − 1})}F₃(m) = {x₃₁, f¹₃(x₃₁, y₃₁), ..., f^n − 1₃(x₃₁, ..., x_{3, n − 1};y₃₁, ..., y_{3, n − 1})}F₃(m) = {x₃₁, f¹₃(x₃₁, y₃₁), ..., f^n − 1₃(x₃₁, ..., x_{3, n − 1};y₃₁, ..., y_{3, n − 1})}F₃(m) = {x₃₁, f¹₃(x₃₁, y₃₁), ..., f^n − 1₃(x₃₁, ..., x_{3, n − 1};y₃₁, ..., y_{3, n − 1})}

The encoding system is used as follows. The strategies F₂ and F₃ are fixed beforehand so as to optimize the transmission from terminal 1 to terminal 3 of an arbitrarily selected message m. If the message m is selected the sender at terminal 1 uses the strategy F₁(m). The function f^k − 1₁ specifies the next input x_1k at terminal 1 on the basis of the message m to be transmitted an the observed outputs y₁₁, ..., y_{1, k − 1} at terminal 1 up to the current time k − 1. Instead of using the encoding function F₁(m) for a given message m we shall often use a sequence X₁(m) of input letters which do not depend on the received letters at terminal 1, i.e., X₁(m) = (x₁₁, ..., x_1n) ∈ Aⁿ₁. The function f^k − 1₂ specifies the next input letter x_2k at terminal 2 on the basis of the transmitted sequence x₂₁, ..., x_{2, k − 1} and the received sequence y₂₁, ..., y_{2, k − 1} at terminal 2 up to the current time. \mathchoicex_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1}) Similarly the function f^k − 1₃ determines the input x_3k as a function of previous inputs x₃₁, ..., x_{3, k − 1} and preivous outputs y₃₁, ..., y_{3, k − 1} at terminal 3. As a special case we shall often take the strategy F₃ to be a sequence X₃ of input letters which do not depend on the received letters at terminal 3, i.e., X₃ = (x₃₁, ..., x_3n) ∈ Aⁿ₃. (Забележи дека само за терминалот 2 нема специјален кејс. Претпоставувам дека тоа е така затоа што тој терминал е само реле.)

To a given encoding system of word length n for transmitting M messages from terminal 1 to terminal 3 there corresponds a decoding system at terminal 3, consisting of M disjoint subsets of Bⁿ₃: D₁, ..., D_M. If the received sequence y₃₁, ..., y_3n lies in D_j the person at terminal 3 decides message j was sent at terminal 1. (Замисли сценарио слично на проблемот од T. Cover EIT со повторување на влезните симболи-имаше пример со три бита) Together an encoding and decoding system constitute a code. In order to compute the error probability for a given code we first need the conditional probabilities for operating the channel n times with the strategies F₁(m), F₂ and F₃.

For this purpose we define for a given d.m. three terminal channel P(y₁, y₂, y₃|x₁, x₂, x₃) and each n ≥ 1 a derived three-terminal channel K_n. An input letter at terminal t for the derived channel K_n is a strategy F_t for choosing a sequence of n consecutive inputs to the memoryless channel P(y₁y₂y₃|x₁x₂x₃). Thus

(23) F_t = {x_t1, f¹_t(x_t1, y_t1), .., f^n − 1_t(x_t1, ...x_{t, n − 1};y_t1, ..., y_{t, n − 1}}

where \strikeout off\uuline off\uwave offf^n − 1_t(x_t1, ...x_{t, n − 1};y_t1, ..., y_{t, n − 1}) represents any function from the first k − 1 transmitted input letters and the first k − 1 observed output letters at terminal t into the next input letter x_tk and x_t1 is the first transmitted letter of the sequence; t = 1, 2, 3.

An output letter for channelK_n at terminal t is is an n-tuple Y_t = (y_t1, ..., y_tn) ∈ Bⁿ_t. The conditional probability of receiving the output (Y₁, Y₂, Y₃) over channel K_n if the input (F₁F₂F₃) is sent, is denoted by Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) and is precisely the probability of receiving \strikeout off\uuline off\uwave off(Y₁, Y₂, Y₃) during n operations of the memoryless channel P(y₁, y₂, y₃|x₁x₂x₃) if the inputs to this channel are determined by the strategies F₁, F₂ and F₃. Thus channel K_n is itself a d.m. three-terminal channel with channel probabilities defined by:

(24) 1Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ⁿ∏_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1}); f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

A special case of the derived channel K_n arises if the strategies F₁, F₂ and F₃ are replaced by sequences X₁X₂ and X₃ , respectively, of tinput letters whic do not depend on the received letters at each particular terminal, i.e., X_t = (x_t1, ..., X_tn) ∈ Aⁿ_t; t = 1, 2, 3. The derived channel then reduces to the memoryless n-extension of P(y₁, y₂, y₃|x₁x₂x₃) which has conditionla probabilitties defined by 1↑. Channel K₁ is identical with:

P(y₁, y₂, y₃|x₁x₂x₃).

To the three-terminal channel K_n there correspond vairous collections of subchannels similar to the subchannels defined in Section 2 in connection with the single channel P(Y₁Y₂Y₃|F₁F₂F₃) by keeping the input strategies at one or two terminals fixeed at particular choices. We consider here three different tuypes of subchannels.

(i) For each fixed pair of strategies (F₂, F₃) the collection of conditional probabilities Pⁿ(Y₃|F₁|F₂F₃) defiened by:

(25) Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃)

is a d.m channel with inputs F₁ and outputs Y₃. Its capacity is denoted by C_n(1, 3|F₂F₃) and

C_n(1, 3) = max_F₂F₃C_n(1, 3|F₂F₃)

(ii) For each fixed pair of strategies (F₂, F₃) the collection of conditional probabilities Pⁿ(Y₂Y₃|F₁|F₂F₃) defiened by:

(26) Pⁿ(Y₂Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Pⁿ(Y₁Y₂Y₃|F₁F₂F₃)

is a d.m channel with inputs F₁ and outputs (Y₂Y₃). Its capacity is denoted by C_n(1, 3|F₂, F₃) and

C_n(1, (2, 3)) = max_F₂F₃C_n(1, (2, 3)|F₂F₃)

(iii) For each fixed pair of strategies F₃ the collection of conditional probabilities Pⁿ(Y₃|F₁F₂|F₃) defiened by:

(27) Pⁿ(Y₃|F₁F₂|F₃) = ⎲⎳_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃)

is a d.m channel with inputs (F₁, F₂) and outputs Y₂. Its capacity is denoted by C_n((1, 2), 3|F₃) and

C_n(1, (2, 3)) = max_F₃C_n((1, 2), 3|F₃)

The error probability for a given code will now be defined with the aid of the conditioal probabilitties 25↑. A (1, 3) -code (n, M, λ) for transmission of any of M ≥ 1 messages of word length n from terminal 1 to terminal 3 over a d.m three-terminal channel P(y₁, y₂, y₃|x₁, x₂, x₃) consist of M encoding functions F₁(1), ..., F₁(M) at terminal 1; a pair of fixed strategies F₂ and F₃ at terminals 2 and 3, respectively; and M decoding subsets D₁, ..., D_M at terminal 3 such that

⎲⎳_{y_{3 ∈ D_m}}Pⁿ(Y₃|F₁(m)|F₂, F₃) ≥ 1 − λ for m = 1, ..., M

Thus, using such a code, the probability that any message transmitted at terminal 1 will be decoded incorrectly at terminal 3 is ≤ λ. A number R(1, 3) ≥ 0 is called an attainable rate for transmission in the 1 − 3 direction over a d.m. three-teminal channel K if there exists a sequence of (1, 3)-codes (n, M_n, λ_n) for K with M_n ≥ 2^nR(1, 3) and such that λ_n → 0.

The transmisstion capacity for sending in the 1-3 direction over channel K is denoted by \mathchoiceC(1, 3)C(1, 3)C(1, 3)C(1, 3) and deifined as the upper bound of the set of attainable rates R(1, 3).

The capacities C_n(1, 3), C_n[1, (2, 3)] , and C_n[(1, 2), 3] above are defined analogously to the single-letter capacities C₁(1, 3), C₁[1, (2, 3)] and C₁[(1, 2), 3]. They correspond to one operation of the derived d.m. channel K_n. Therefore all inequalityies of Section 4 for single letter capacities carry over to coresponding inequalities for n-letter capacities. In particular, it follows from Lemmas 4.1 and 4.3 that, for all n ≥ 1,

(28) C_n(1, 3) ≤ C_n[1, (2, 3)]

and

(29) C_n(1, 3) ≤ C_n[(1, 2), 3])

C_n(1, 3) is the capacity of the „best” d.m. channel Pⁿ(Y₃|F₁|F₂, F₃) as F₂ and F₃ vary over strategies of length n. The memoryless k-extension of this best channel is a d.m. channel of the form P^nk(Y₃|F₁|F₂, F₃) with capacity equal to k⋅C_n(1, 3) . The capacity of the best d.m. channel P^nk(Y₃|F₁|F₂F₃) as F₂ and F₃ vary over strategies of length nk is equal to C_nk(1, 3). The strategies of length nk include as special cases those strategies whose functional influence involves only blocks of length n. Therefore

(30) \mathchoice(C_n(1, 3))/(n) ≤ (C_nk(1, 3))/(nk)(C_n(1, 3))/(n) ≤ (C_nk(1, 3))/(nk)(C_n(1, 3))/(n) ≤ (C_nk(1, 3))/(nk)(C_n(1, 3))/(n) ≤ (C_nk(1, 3))/(nk)

for all positive integers n and k. Ова ми се коси со доказот на Theorem 7.3 доколку n=k=1.

The channel capacity for transmition in the 1 − 3 direction is for any d.m three-terminal channel defined by

(31) C(1, 3) = sup_n(C_n(1, 3))/(n)

in section 7 is shown that C(1, 3) is actually the transmission capacity for sending from terminal 1 to termina 3, i.e, C(1, 3) = C(1, 3). It is a consequence of Theorems 7.1and 7.2 below that

(32) \mathchoiceC(1, 3) = lim_{n → ∞}(C_n(1, 3))/(n)C(1, 3) = lim_{n → ∞}(C_n(1, 3))/(n)C(1, 3) = lim_{n → ∞}(C_n(1, 3))/(n)C(1, 3) = lim_{n → ∞}(C_n(1, 3))/(n)

In next sextion we establish a necessary and sufficient condition under whih C(1, 3) > 0.

6 A necessary and sufficient condition for a positive channel capacity

In this section we derive the following necessary and sufficient condition for positive channel capacity.

Theorem 6.1

C(1, 3) > 0 if and only if both C₁[1, (2, 3)] > 0 and C₁[(1, 2), 3] > 0. Alternatively, C(1, 3) = 0 if eather C₁[1, (2, 3)] = 0 or C₁[(1, 2), 3] = 0. MMV

For the proof we shall need Lemmas 6.1 and 6.2 below.

Lemma 6.1

If C₁[1, (2, 3)] = 0 then C_n[1, (2, 3)] = 0 for all n ≥ 1. Similarly, if C₁[(1, 2)3] = 0 then C_n[(1, 2), 3] = 0 for all n ≥ 1.

Proof. We only prove the first statement. Let \strikeout off\uuline off\uwave offC₁[1, (2, 3)] = 0. \uuline default\uwave defaultThis implies that for each fixed pair (y₂, y₃) the conditional probability P(y₂, y₃|x₁x₂x₃) remains the same as x₁ varies\strikeout off\uuline off\uwave off Дали тоа значи дека всушност y₂, y₃ не зависат од x₁??? Така всушност ќе излезе дека I(X₁;Y₂Y₃) = 0. Да токму тоа значи. Види изведување подолу. .

\strikeout off\uuline off\uwave offWe need to show C_n[1, (2, 3)] = 0 for all n ≥ 1, i.e., for each fixed pair of strategies (F₂, F₃) the d.m. channel Pⁿ(Y₂, Y₃|F₁|F₂, F₃) has identical rows as F₁ varies over all inputs strategies at terminal 1. From 24↑ and 25↑ we have

\strikeout off\uuline off\uwave offPⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ∏ⁿ_k = 1P{y_1ky_2k, y_3k|f^k − 1₁f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

(33) Pⁿ(Y₂Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Pⁿ(Y₁Y₂Y₃|F₁F₂F₃)

Pⁿ(Y₂Y₃|F₁|F₂F₃) = ⎲⎳_{y₁₁y_12,...y_1n}ⁿ∏_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

Let now n, F₂, F₃, Y₂ and Y₃ all be fixed. Since C₁[1, (2, 3)] = 0,

P(y_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1})f^k − 1₂(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₃(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}));

does not depend on the actual value of \strikeout off\uuline off\uwave offf^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}) therefore 33↑ can be rewriten as

Pⁿ(Y₂Y₃|F₁|F₂F₃) = ∏ⁿ_k = 1P{y_2k, y_3k|f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

where the input sequence X₁ = (x₁₁, ..., x_1n) is chosen arbitrarily. This holds for all choices of F₁, thus Pⁿ(Y₂Y₃|F₁|F₂F₃) stays same as F₁ varies. This completes the proof of the first part of the lemma (C_n[1, (2, 3)] = 0). The proof of the second part is very similar.

Lemma 6.2

If C₁(1, 3) = 0, C₁[1, (2, 3)] > 0 and C₁(2, 3) > 0 then \mathchoiceC₂(1, 3) > 0C₂(1, 3) > 0C₂(1, 3) > 0C₂(1, 3) > 0

Proof. C₁[1, (2, 3)] > 0 implies there exists a pair (x₂₀, x₃₀) of input letters and a pair (y₂₀, y₃₀) of output letter at terminals 2 and 3 and two different input letters x_1i and x_1j at terminal 1 such that

α_i = P(y₂₀, y₃₀|x_1i, x₂₀, x₃₀) ≠ P(y₂₀, y₃₀|x_1j, x₂₀, x₃₀) = α_j, (Ова следи од \strikeout off\uuline off\uwave offC₁[1, (2, 3)] > 0) say.

Now

Let

Then β_j − β_i = α_i − α_j ≠ 0.

Since \mathchoiceC₁(2, 3) > 0C₁(2, 3) > 0C₁(2, 3) > 0C₁(2, 3) > 0 there exist input letter x₁₀’ and x₃₀’ at terminal 1 and terminal 3 , respectively, one output letter y₃₀’ at terminal 3 and two different input letters x_2k and x_2l at terminal 2, such that \mathchoicec_k = P(y₃₀’|x₁₀’, x_2k, x₃₀’) ≠ P(y₃₀’|x₁₀’, x_2l, x₃₀’) = c_lc_k = P(y₃₀’|x₁₀’, x_2k, x₃₀’) ≠ P(y₃₀’|x₁₀’, x_2l, x₃₀’) = c_lc_k = P(y₃₀’|x₁₀’, x_2k, x₃₀’) ≠ P(y₃₀’|x₁₀’, x_2l, x₃₀’) = c_lc_k = P(y₃₀’|x₁₀’, x_2k, x₃₀’) ≠ P(y₃₀’|x₁₀’, x_2l, x₃₀’) = c_l, say. Clearly

(34) c_k(α_i − α_j) ≠ c_l(β_j − β_i)

We will now show the exisstence of a d.m channel of the form P²(Y₃|F₁|F₂, F₃) which has at least two different rows and therefore (каналната матрицa треба да има различни редици за да капацитетот е различен од 0 (а не транспонираната канална матрица). Види изведуање во box-от подолу) has capacity different form zero. The strategy \mathchoiceF₂ = {x₂₁, f¹₂(y₂₁)}F₂ = {x₂₁, f¹₂(y₂₁)}F₂ = {x₂₁, f¹₂(y₂₁)}F₂ = {x₂₁, f¹₂(y₂₁)} is defined by \mathchoicex₂₁ = x₂₀x₂₁ = x₂₀x₂₁ = x₂₀x₂₁ = x₂₀ and

(35) f¹₂(y₂₁) = ⎧⎨⎩ x_2k if y₂₁ = y₂₀ x_2l if y₂₁ ≠ y₂₀

⎡⎢⎢⎢⎣ p(y₁) p(y₂) p(y₃) ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ p₁₁ p₂₁ p₃₁ p₁₂ p₂₂ p₃₂ p₁₃ p₂₃ p₃₃ ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₁) p(x₂) p(x₃) ⎤⎥⎥⎥⎦ ∑³_j = 1p(y_j|x_i) = ∑³_j = 1p_i, j = 1 i = 1, 2, 3 кога ќе пратиш некој влезен симбол на излезмора да добиеш нешто!!!

⎡⎢⎢⎢⎣ p(y₁) p(y₂) p(y₃) ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ p₁ p₂ p₃ p₁ p₂ p₃ p₁ p₂ p₃ ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₁) p(x₂) p(x₃) ⎤⎥⎥⎥⎦
p(y₁) = ∑³_i = 1p_ip(x_i) p(y₂) = ∑³_i = 1p_ip(x_i) p(y₃) = ∑³_i = 1p_ip(x_i) ⇒ p(y₁) = p(y₂) = p(y₃)
H(Y) = log₂(M) = log(3)
H(Y|X) = ∑_ip(x_i)⋅H(Y|x_i) = p(x₁)⋅H(Y|x₁) + p(x₂)⋅H(Y|x₂) + p(x₃)⋅H(Y|x₃) = p(x₁)⋅3⋅p₁log₂((1)/(p₁)) + p(x₂)⋅3⋅p₂log₂((1)/(p₂)) + p(x₃)⋅3⋅p₃log₂((1)/(p₃)) ≠ H(Y) ⇒ C > 0
Значи треба нетранспонираната канална матрица да има исти редици за да капацитетот биде 0!!!
⎡⎢⎢⎢⎣ p(y₁) p(y₂) p(y₃) ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ p₁ p₁ p₁ p₂ p₂ p₂ p₃ p₃ p₃ ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₁) p(x₂) p(x₃) ⎤⎥⎥⎥⎦ Π = ⎡⎢⎢⎢⎣ p₁ p₂ p₃ p₁ p₂ p₃ p₁ p₂ p₃ ⎤⎥⎥⎥⎦
p(y₁) = p₁ p(y₂) = p₂ p(y₃) = p₃ ⇒ H(Y) = ∑³_i = 1p_ilog₂((1)/(p_i))
H(Y|X) = ∑_ip(x_i)⋅H(Y|x_i) = p(x₁)⋅H(Y|x₁) + p(x₂)⋅H(Y|x₂) + p(x₃)⋅H(Y|x₃) = p(x₁)⋅∑³_i = 1p_ilog₂((1)/(p_i)) + p(x₂)⋅∑³_i = 1p_ilog₂((1)/(p_i)) + p(x₃)⋅∑³_i = 1p_ilog₂((1)/(p_i)) = ∑³_i = 1p_ilog₂((1)/(p_i))
H(Y|X) = H(Y) ⇒ C = H(Y) − H(Y) = 0

Thus the first input letter at terminal 2 is held at x₂₀ and the second input letter is x_2k or x_2l according to wheter the first observed output letter y₂₁ was equal to y₂₀ or not. The strategy \mathchoiceF₃ = {x₃₁, f¹₃}F₃ = {x₃₁, f¹₃}F₃ = {x₃₁, f¹₃}F₃ = {x₃₁, f¹₃} is defined by \mathchoicex₃₁ = x₃₀x₃₁ = x₃₀x₃₁ = x₃₀x₃₁ = x₃₀ and \mathchoicef¹₃ = x^’₃₀f¹₃ = x^’₃₀f¹₃ = x^’₃₀f¹₃ = x^’₃₀. The inputs F₁ at terminal 1 are chosen to be sequences X₁ = (x₁₁x₁₂) of input letters. For this choice of F₂ and F₃ and for every \mathchoiceX₁ = (x₁₁, x₁₂)X₁ = (x₁₁, x₁₂)X₁ = (x₁₁, x₁₂)X₁ = (x₁₁, x₁₂) and \mathchoiceY₃ = (y₃₁, y₃₂)Y₃ = (y₃₁, y₃₂)Y₃ = (y₃₁, y₃₂)Y₃ = (y₃₁, y₃₂) we have:

\strikeout off\uuline off\uwave offPⁿ(Y₃|F₁|F₂F₃) = ∑_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) ова е од 25↑

\strikeout off\uuline off\uwave offPⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ∏ⁿ_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

Вторава ако се замени во првава се добива:

\strikeout off\uuline off\uwave off

(36) 1 Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}); f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

1P²(Y₃|F₁|F₂, F₃) = ⎲⎳_{y₂₁, y₂₂}P(y₂₁, y₃₁|x₁₁, x₂₀, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, f¹₂(y₂₁), x^’₃₀) = = P(y₃₂|x₁₂, x_2k, x^’₃₀)P(y₂₀, y₃₁|x₁₁, x₂₀, x₃₀) + P(y₃₂|x₁₂, x_2l, x^’₃₀)⋅\cancelto proof is below!!!{P(y₃₁|x₁₁, x₂₀, x₃₀) − P(y₂₀, y₃₁|x₁₁, x₂₀, x₃₀)}

\strikeout off\uuline off\uwave offPⁿ(Y₃|F₁|F₂F₃) = ∑_Y₁Y₂∏ⁿ_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

Pⁿ(Y₃|F₁|F₂F₃) = ∑_Y₂∏²_k = 1P{y_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

F₂ = {x₂₁, f¹₂(y₂₁)} f¹₂(y₂₁) = ⎧⎨⎩ x_2k if y₂₁ = y₂₀ x_2l if y₂₁ ≠ y₂₀

1Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_{y₂₁y₂₂}P{y₂₁, y₃₁|f⁰₁(x₁₁, x_1, 0;y₁₁, ..., y_1, 0);f⁰₂(x₂₁, ..., x_2, 0;y₂₁, ..., y_2, 0);f⁰₃(x₃₁, ..., x_3, 0;y₃₁, ..., y_3, 0)}⋅ ⋅P{y₂₂, y₃₂|f¹₁(x₁₁;y₁₁);f¹₂(x₂₁;y₂₁);f¹₃(x₃₁;y₃₁)}

1 Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_{y₂₁y₂₂}P{y₂₁, y₃₁|\canceltox₁₁ from F₁ = (x₁₁, x₁₂)f⁰₁(x₁₁, x_1, 0;y₁₁, y_1, 0); \canceltox₂₁ = x₂₀ from F₂ = {x₂₁, f¹₂(y₂₁)}f⁰₂(x₂₁, x_2, 0;y₂₁, y_2, 0); \canceltox₃₁ = x₃₀ from F₃ = (x₃₁, f¹₃)f⁰₃(x₃₁, x_3, 0;y₃₁, y_3, 0)} ⋅ P{y₂₂, y₃₂|\canceltox₁₂ from F₁ = (x₁₁, x₁₂)f¹₁(x₁₁;y₁₁); \canceltof¹₂(y₂₁) from F₂ = {x₂₁, f¹₂(y₂₁)}f¹₂(x₂₁;y₂₁); \canceltof¹₃ = x^’₃₀ from F₃ = (x₃₁, f¹₃)f¹₃(x₃₁;y₃₁)}

Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_{y₂₁y₂₂}P{y₂₁, y₃₁|x₁₁, x₂₀, x₃₀}⋅P{y₂₂, y₃₂|x₁₂;f¹₂(y₂₁);x₃₀’}

(37) Pⁿ(Y₃|F₁|F₂F₃) = P{y₂₀, y₃₁|x₁₁, x₂₀, x₃₀}⋅P{y₃₂|x₁₂;\mathchoicex_2kx_2kx_2kx_2k;x₃₀’} + {P{y₃₁|x₁₁, x₂₀, x₃₀} − P{y₂₀, y₃₁|x₁₁, x₂₀, x₃₀}}P{y₃₂|x₁₂;\mathchoicex_2lx_2lx_2lx_2l;x₃₀’}

Првиот член од сумата на LHS е за y₂₁ = y₂₀ a вторито член е за \strikeout off\uuline off\uwave offy₂₁ ≠y₂₀. Разликата на веројатности во вториот член потекнува од тоа \uuline default\uwave defaultшто првата веројатност е сума на веројатностите за сите вредности на y₂₁\strikeout off\uuline off\uwave off (затоа y₂₁ е елиминиран од здружената веројатност). Она што останува од разликата е всушност P{y₂₁, y₃₁|x₁₁, x₂₀, x₃₀} за y₂₁ ≠ y₂₀.

Now choosing Y₃₀ =(y₃₀, y^’₃₀), X₁₀ = (x_1i, x^’₁₀) and X^’₁₀ = (x_1j, x^’₁₀) one has P²(Y₃₀|X₁₀|F₂F₃) = c_kα_i + c_lβ_i.

\strikeout off\uuline off\uwave offc_k = P(y₃₀’|x₁₀’, x_2k, x₃₀’) ≠ P(y₃₀’|x₁₀’, x_2l, x₃₀’) = c_l; α_i = P(y₂₀, y₃₀|x_1i, x₂₀, x₃₀) = P(y₂₀, y₃₀|x_1j, x₂₀, x₃₀) = α_j

β_i = P(y₃₀|x_1i, x₂₀, x₃₀) − P(y₂₀, y₃₀|x_1i, x₂₀, x₃₀) and β_j = P(y₃₀|x_1j, x₂₀, x₃₀) − P(y₂₀, y₃₀|x_1j, x₂₀, x₃₀).

\strikeout off\uuline off\uwave offPⁿ(Y₃ = Y₃₀|F₁ = X₁₀|F₂F₃) = \mathchoiceP{y₂₀, y₃₁|\canceltox_1ix₁₁, x₂₀, x₃₀}P{y₂₀, y₃₁|\canceltox_1ix₁₁, x₂₀, x₃₀}P{y₂₀, y₃₁|\canceltox_1ix₁₁, x₂₀, x₃₀}P{y₂₀, y₃₁|\canceltox_1ix₁₁, x₂₀, x₃₀}⋅\mathchoiceP{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’} + P{\canceltoy^’₃₀y₃₂|x₁₂;x_2l;x₃₀’}⋅{P{\canceltoy₃₀y₃₁|x₁₁, x₂₀, x₃₀} − P{y₂₀, y₃₁|x₁₁, x₂₀, x₃₀}} следи од: 37↑.

\strikeout off\uuline off\uwave offP²(Y₃ = Y₃₀|F₁ = X^’₁₀|F₂F₃) = \mathchoiceP{y₂₀, \canceltoy₃₀y₃₁|\canceltox_1jx₁₁, x₂₀, x₃₀}P{y₂₀, \canceltoy₃₀y₃₁|\canceltox_1jx₁₁, x₂₀, x₃₀}P{y₂₀, \canceltoy₃₀y₃₁|\canceltox_1jx₁₁, x₂₀, x₃₀}P{y₂₀, \canceltoy₃₀y₃₁|\canceltox_1jx₁₁, x₂₀, x₃₀}⋅\mathchoiceP{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’}P{\canceltoy^’₃₀y₃₂|x₁₂;x_2k;x₃₀’} + P{\canceltoy^’₃₀y₃₂|x₁₂;x_2l;x₃₀’}⋅{P{\canceltoy₃₀y₃₁|x₁₁, x₂₀, x₃₀} − P{y₂₀, y₃₁|x₁₁, x₂₀, x₃₀}}

By 34↑ \strikeout off\uuline off\uwave offP²(Y₃₀|X₁₀|F₂F₃) ≠ P²(Y₃₀|X^’₁₀|F₂F₃)

\strikeout off\uuline off\uwave offc_k(α_i − α_j) ≠ c_l(β_j − β_i)

P²(Y₃₀|X₁₀|F₂F₃) − P²(Y₃₀|X^’₁₀|F₂F₃) = c_kα_i + c_lβ_i − c_kα_j − c_lβ_j = c_k(α_i − a_j) − c_l(β_j − β_i) ≠ 0 ⇒ P(Y₃₀|X₁₀|F₂F₃)≠P²(Y₃₀|X^’₁₀|F₂F₃)

hence the channel matrix P²(Y₃|F₁|F₂F₃) has at least two different rows. This implies that C₂(1, 3) > 0 and thus completes the proof of the lemma (Претпоставката на лемата дека \strikeout off\uuline off\uwave offC₁[1, (2, 3)] > 0\uuline default\uwave default е вградена во α_i ≠ α_j) .

Now we turn to the proof of Theorem 6.1. First suppose both C₁[1, (2, 3)] > 0 and C₁[(1, 2), 3] > 0. By Corollary 4.2, C₁[(1, 2), 3] > 0 implies either \strikeout off\uuline off\uwave offC₁(1, 3) > 0 or C(2, 3) > 0. If C₁(1, 3) > 0 then by 30↑ C₂(1, 3) > 0. If C₁(1, 3) = 0 then C₁(2, 3) > 0 and C₂(1, 3) > 0 by Lemma 6.2. In either case C₂(1, 3) > 0 and thus C₁(1, 3) > 0 by 32↑. Conversely, suppose either \uuline default\uwave defaultC₁[1, (2, 3)] = 0 or C₁[(1, 2), 3] = 0. If C₁[1, (2, 3)] = 0 then C_n[1, (2, 3)] = 0 for all n > = 1 by Lemma 6.1. Thus C_n(1, 3) = 0 for all n ≥ 1 by 28↑ and hence C(1, 3) = 0 by 31↑. Similar argument holds if \strikeout off\uuline off\uwave offC₁[(1, 2), 3] = 0. This completes the proof of Theorem 6.1.

7 The coding Theorem and its week converse

We now shot that C(1, 3) is the actual transmission capacity for sending from terminal 1 to terminal 3, i.e., C(1, 3) = C(1, 3). This result follows immedialtely form Theorems 7.1 and 7.2 below.

Theorem 7.1

Let ϵ > 0 and 0 < λ ≤ 1 be arbitrary. For any d.m. three-terminal channel and all n sufficiently large there exists a (1, 3) -code (n, M, λ) with M > 2^{n[C(1, 3) − ϵ]}.

n⋅C(1, 3) − n⋅ϵ < log₂(M) C(1, 3) < (1)/(n)⋅log₂(M) + ϵ

\strikeout off\uuline off\uwave offR = (1)/(n)⋅log(M) ≤ C; M ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < M

Proof. Let m be positive integer such that

(38) (C_m(1, 3))/(m) > C(1, 3) − (ϵ)/(2)

Let F₂ and F₃ be two strategies of length m such that the corresponding d.m. channel P^m(Y₃|F₁|F₂, F₃) has capacity C_m(1, 3). First suppose \mathchoicen = k⋅mn = k⋅mn = k⋅mn = k⋅m, with k a positive integer. A code (k, M, λ) for the d.m.c P^m(Y₃|F₁|F₂, F₃) is clearly a (1, 3)-code (n, M, λ) for the d.m. three-terminal channel P(y₁y₂y₃|x₁x₂x₃). By [7] there exists, for all k sufficiently large, a code (k, M, λ) for channel P^m(Y₃|F₁|F₂F₃) with

M > 2^{k(C_m(1, 3) − t ⁄ 4)} = 2^{n(C_m(1, 3) ⁄ m − t ⁄ 4m)} > 2^{n(C(1, 3) − 3t ⁄ 4)}.

This proves the theorem for n of the form k⋅m.

Now suppose \mathchoicen = km + t 1 ≤ t < mn = km + t 1 ≤ t < mn = km + t 1 ≤ t < mn = km + t 1 ≤ t < m. Proceeding as before, there exists a code (k, M, λ) for the d.m.c. P^m(Y₃|F₁|F₂, F₃) with

M > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{n⋅((n − t) ⁄ n)⋅(C(1, 3) − 3⋅t ⁄ 4)} > 2^{n(C(1, 3) − t)}.

Ова не успеав да го докажам подолу!!!

Прв обид:

1((n − t) ⁄ n)⋅(C(1, 3) − 3⋅t ⁄ 4m) = (1)/(n)(nC − 3⋅t⋅n ⁄ 4m − t⋅C − 3⋅t² ⁄ 4m) = ⎛⎝C − 3⋅t ⁄ 4m − (t⋅C)/(n) − 3⋅t² ⁄ (4⋅n⋅m)⎞⎠ = |t = n − km| = ⎛⎝C − 3⋅(n − km) ⁄ 4m − ((n − km)⋅C)/(n) − 3⋅(n − km)² ⁄ (4⋅n⋅m)⎞⎠ = ⎛⎝C − (3⋅n)/(4m) + (3k)/(4) − C + (mk)/(n)C − (3⋅(n² − 2nkm + k²m²))/(4⋅n⋅m)⎞⎠

Втор обид:

1((n − t) ⁄ n)⋅(C(1, 3) − 3⋅t ⁄ 4m) ≥ (1)/(n)(n − t)(C(1, 3) − 3⋅m ⁄ 4m) = (1)/(n)(n − t)⎛⎝C(1, 3) − (3)/(4)⎞⎠ = (1 − (t)/(n))⋅⎛⎝C(1, 3) − (3)/(4)⎞⎠ > (1 − (t)/(n))⋅(C(1, 3) − 1) = C(1, 3) − 1 − (t)/(n)⋅C(1, 3) + (t)/(n) > C(1, 3) − 1 − (t)/(n)⋅C(1, 3) = |n = km + t| = C(1, 3) − (km + t)/(n) − (t)/(n)⋅C(1, 3) = C(1, 3) − (km)/(n) − (t)/(n)(1 + C(1, 3))

((n − t) ⁄ n)⋅(C(1, 3) − 3⋅t ⁄ 4m) ≥ (1)/(n)(n − t)(C(1, 3) − 3⋅m ⁄ 4m) = (1)/(n)(n − t)(C(1, 3) − 3 ⁄ 4) = (1)/(n)(n − m)(C(1, 3) − 3 ⁄ 4) > (1)/(n)(n − mk)(C(1, 3) − 3 ⁄ 4) = (t)/(n)(C(1, 3) − 3 ⁄ 4)
Трет обид:
\mathchoiceM > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{k⋅m(C(1, 3) − 3⋅t ⁄ 4)} > 2^{k⋅m(C(1, 3) − t)}M > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{k⋅m(C(1, 3) − 3⋅t ⁄ 4)} > 2^{k⋅m(C(1, 3) − t)}M > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{k⋅m(C(1, 3) − 3⋅t ⁄ 4)} > 2^{k⋅m(C(1, 3) − t)}M > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{k⋅m(C(1, 3) − 3⋅t ⁄ 4)} > 2^{k⋅m(C(1, 3) − t)} ова е најблиску што може до доказ.

\strikeout off\uuline off\uwave offM > 2^{(n − t)(C(1, 3) − 3⋅t ⁄ 4)} > 2^{(n − m)(C(1, 3) − 3⋅t ⁄ 4)} = 2^{n(C(1, 3) − 3⋅t ⁄ 4)}⋅2^{− t(C(1, 3) − 3⋅t ⁄ 4)}

Четврти обид:
(C_nk(1, 3))/(nk) > (C_n(1, 3))/(n)
((n − t) ⁄ n)⋅(C(1, 3) − 3⋅t ⁄ 4) ≥ (1)/(n)(n − t)(C(1, 3) − 3⋅m ⁄ 4m) = (1)/(n)(n − t)(C(1, 3) − 3 ⁄ 4)

for all k sufficiently large. This completes the proof of the theorem.

Theorem 7.2

For any d.m. three-terminal channel a (1, 3)-code (n, M, λ) statisfies

(39) logM ≤ (n⋅C(1, 3) + 1)/(1 − λ)

Proof. We actually have somewhat stronger inequality

(40) logM ≤ (n⋅C_n(1, 3) + 1)/(1 − λ)

which follows form [7], a result which is due to Fano [2].

As a consequence we nao have:

Theorem 7.3

For any d.m. three-terminal channel we have

(41) C(1, 3) = lim_{n → ∞}(C_n(1, 3))/(n)

Proof. Let ϵ > 0 be arbitrary. From Theorem 7.1 and inequality 40↑ we have that for n sufficiently lareg

2^{n(C(1, 3) − ϵ)} < 2^{C_n(1, 3) + nϵ}

\strikeout off\uuline off\uwave off\mathchoiceR = (1)/(n)⋅log(M) ≤ C; M ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < MR = (1)/(n)⋅log(M) ≤ C; M ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < MR = (1)/(n)⋅log(M) ≤ C; M ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < MR = (1)/(n)⋅log(M) ≤ C; M ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < M

M > 2^{n[C(1, 3) − ϵ]} logM ≤ (n⋅C_n(1, 3) + 1)/(1 − λ) (C_nk(1, 3))/(nk) > (C_n(1, 3))/(n)

n(C(1, 3) − ϵ) < C_n(1, 3) + nϵ; nC(1, 3) − nϵ < C_n(1, 3) + nϵ; nC(1, 3) − 2nϵ < C_n(1, 3); C(1, 3) − 2ϵ < (1)/(n)⋅C_n(1, 3);

This together with the definition of C(1, 3) implies

C(1, 3) − 2ϵ < (C_n(1, 3))/(n) ≤ C(1, 3)

for sufficiently large n . This proves the theorem.

8 Lower bounds on the capacity

The capacity C(1, 3) can be described by the limiting expression 32↑ which is hard to evaluate. In this section we derive several lower bonunds on C(1, 3) which are more easily evaluated since they involve a maximizing process over single inputs and outputs to the channel only. Define R₁R₂R₃ and R₄ as follows:

(42) R₁ = C₁(1, 2),

(43) R₂ = ⎧⎨⎩ (C₁(1, 2)C₁(2, 3))/(C₁(1, 2) + C₁(2, 3)) , if C₁(1, 2) > 0 and C₁(2, 3) > 0 0 otherwise

(44) R₃ = (C₁[1, (2, 3)]⋅C₁(2, 3))/(C₁(2, 3) + logb₂)

\strikeout off\uuline off\uwave off

(45) R₄ = (C₁[(1, 2), 3]⋅C₁(1, 2))/(C₁(1, 2) + loga₂)

Here a₂ and b₂ denote the size of the input and ouptut alphabet respecitvely at terminal 2. We will show that R₁, R₂, R₃ and R₄ are lower bounds on C(1, 3) follows immediately form coding theorems 8.1 8.2 and 8.3 below. Which of the lower bounds is largest depends on the praticular channel under consideration. Numerical examples are given in 6↓. There we have evaluated for each example of Section 3 the lower bounds R₁, R₂, R₃ and R₄. In Section 9 another lower bound R₅ is obtained, which applies only to channels with a certain symmetric structure. We have included in the table the values of R₅ as well, for those examples (1 and 2) to which this bound applies. For sake of completnes we have includet in the tabel also for eqach example the values of the upper bounds U and U’ which are derived in Section 10. As can be seen form the table, it turns out that for each example the largest lower bound coincides wiht the smallest upper bound. The capacity C(1, 3) is clearly equal to the common value. The values of C(1, 3) are given in last column of the table.

Table 6 Table VII

We now state and prove the coding theorems 8.1, 8.2 and 8.3.

Theorem 8.1

Let ϵ > 0 and 0 ≤ λ ≤ 1 be arbitrary. For any d.m. three-terminal channel and all n sufficiently large there exists a (1, 3) -code (n, M, λ) with:

(46) M > exp₂{n(R₂ − ϵ)}.

Proof. Assume C₁(1, 2) > 0 and C₁(2, 3) > 0. There exist a pair (x₂₀, x₃₀) of inputs letters such that the d.m.c. s₁ with channel probabilities given by P(y₂|x₁|x₂₀, x₃₀) has capacity C₁(1, 2). Let λ₀ = (λ)/(2). For n₁ sufficintly large there exists a code (n₁, M₁, λ₀) for transmitting M₁ codewords over s₁ with rate arbitrarily close to C₁(1, 2). Similarly there exists a pair (x₁₀’, x₃₀’) such that for n₂ sufficienlty large there exists a code (n₂, M₂, λ₀) with rate arbitrarily close to C₁(2, 3) for d.m.c. s₂ whose channel probabilities are defined by P(y₃|x₂|x₁₀’, x₃₀’). We chose n₁ and n₂ sufficiently large such that the above codes exist and such that

(47) M₂ ≥ M₁ > exp₂{(n₁ + n₂)(R₂ − ϵ)}.

(MMV)

R = (1)/(n)⋅log(M) ≤ C; \mathchoiceM ≤ 2^nCM ≤ 2^nCM ≤ 2^nCM ≤ 2^nC R = C − ϵ; M ≤ 2^{n(R + ϵ)}; R − ϵ < (1)/(n)⋅log(M); n⋅(R − ϵ) < log(M); 2^{n⋅(R − ϵ)} < M
Ако сакаш да нема грешки при преносот т.е. тие да бидат произволно мали треба да се придржуваш кон M ≤ 2^nC.
Присети се на noisy typewriter!!! Тој ја грешеше секоја втора буква. Капацитетот на каналот е log₂(13). Големината на кодната книга треба да биде M ≤ 2^log₂(13) = 13 . Со други зборови во приемникот во случај на ваков канал можеш да препознаеш најмногу 13 различни кодни симболи.

The two codes may be combined to a (1, 3)-code (n₁ + n₂, M₁, λ) in the following way. If the message m is to be sent from terminal 1 to terminal 3, first the m-th codeword of the first code is transmitted over channel s₁. After n₁ channel operations this message is decoded as message j, say, at terminal 2. Next the j-th codeword of the second code is sent at terminal 2, using channel s₂. The received sequence of length n₂ at terminal 3 is decoded as message k, say. Thus after n₁ + n₂ channel operations terminal 3 concludes that message k was originally sent at terminal 1. The total probability of an error in decoding is bounded by 2λ₀ = λ. The code of length n₁ + n₂ with M₁ codewords at terminal 1, consisting of all words of the first code followed by a sequence of n₂ repetitions of the letter x₁₀’ has a rate at least as large as R₂ and error probability bounded by λ. This proves the theorem of n of the form n₁ + n₂ where n₁ and n₂ are chosen so as to satisfy 47↑. For general n we can reduce to the above case by transmitting, a few essentially dummy letters.

Theorem 8.2

Let ϵ > 0 and 1 ≤ λ ≤ 1 be arbitrary. For any d.m. three-terminal channel and all n sufficiently large there exists a (1, 3)-code (n, M, λ) with

(48) M > exp₂{n⋅(R₃ − ϵ)}.

Proof. We proceed as in the proof of Theorem 8.1. Assume C₁[1, (2, 3)] > 0 and C₁(2, 3) > 0. There exist pair (x₂₀, x₃₀) of input letters such that the d.m.c s₁ with channel probabilities P(y₂, y₃|x₁|x₂₀, x₃₀) has capacity C₁[1, (2, 3)] > 0. Let λ₀ = (λ)/(2). For all n₁ sufficiently large there exists code (n₁, M₁, λ₀) for channel s₁ with rate arbitrary close to \strikeout off\uuline off\uwave offC₁[1, (2, 3)]. Similarly there exist a pair (x₁₀’, x₁₀’) such that for n₂ sufficiently large there exists a code (n_2,M₂, λ₀) with rate arbitrarily close to C₁(2, 3) for the d.m.c s₂ whose channel probabilities are given by P(y₃|x₂|x₁₀’, x₃₀’). We chose n₁ and n₂ sufficiently large such that above codes exist and such that the following inequalities are satisfied:

(49) M₁ > exp₂{(n₁ + n₂)⋅(R₃ − ϵ)}

(50) M₂ ≥ b^n₁₂

We now describe how these two codes can be combined to a (1, 3)-code (n₁ + n₂, M₂, λ). If message m is to be sent from terminal 1 to terminal 3 the m-th codeword of the first code is transmitted over channel s₁. A chance sequence (y₂₁, ...y_2n₁) of n₁ letters is received at terminal 2 and a sequence (y₃₁, ..., y_3n₁) is received at terminal 3. Since M₂ ≥ b^n₁₂ there exists a one-to-one mapping form the space of all received sequences at terminal 2 into the set of codewors of the second code. Supppose this mapping associates the j-th codeword of the second code with the sequence \strikeout off\uuline off\uwave off(y₂₁, ...y_2n₁). Then this codeword is transmitted at terminal 2, using channel s₂ ,during the next n₂ channel operations. A chanel sequence (y_{3, n₁ + 1}, ..., y_{3, n₁ + n₂}) is received at terminal 3 and is decoded into message i, say, using the decoding sets of the second code. If the above mapping associates the message i with the sequence (y₂₁’, ..., y_2n₁’), terminal 3 concludes that this sequence was received at terminal 2 during the first n₁ channel operations. Using the decoding sets of the first code terminal 3 decodes the sequence (y₂₁’, ..., y_2n’;y₃₁, ..., y_3n₁) of n₁ pairs of received symbols into message k, say. Terminal 3 then concludes that message k was originally sent at terminal 1. The total probability of an error in decoding is bounded by 2λ₀ = λ. This proves the theorem for n of the form n₁ + n₂ where n₁ and n₂ are chosen so that 49↑ and 50↑ are satisfied. The case for general n can easily be reduced to the above case.

Theorem 8.3

Let ϵ > 0 and 1 ≤ λ ≤ 1, be arbitrary. For any d.m. three-terminal channel and all n sufficiently large there exists a (1, 3)-code (n, M, λ) with

(51) M > exp₂{n(R₄ − ϵ)}.

Proof. Proceeding as before we assume that C₁(1, 2) > 0 and C₁[(1, 2), 3] > 0. There exists a pari (x₂₀, x₃₀) of input letters such that the d.m.c. s_1 with channlel probabilities P(y₂|x₁|x₂₀x₃₀) has capacity C₁(1, 2). Let λ₀ = (λ)/(2). For al n₁ sufficienlty large there exists a code (n₁, M₁, λ₀) for channel s₁ with rate arbitrarily close to C₁(1, 2). similarly there exists an input letter x₃₀’ such that for n₂ sufficiently large there exist a code (n₂, M₂, λ₀) with rate arbitrarily close to C₁[(1, 2), 3] fro channel s₂ whose channel probabilities are given by P(y₃|x₁x₂|x₃₀’). We choose n₁ and n₂ sufficiently large such that the above codes exist and such that the following inequalityies are satisfied:

(52) M₁ ≥ a^n₂₂

(53) M₂ ≥ exp₂{(n₁ + n₂)(R₄ − ϵ)}

The two codes can be combined to a (1, 3)-code (n₁ + n₂, M₂, λ) as follows. If the sender at terminal 1 wants to send message m to terminal 3 he looks up the m-th codeword of the secodn code. Each codeword of the second code consist of pair of input sequences each of length n₂. Suppose the m-th codeword of the second code is the paricular sequence (x₁₁, ..., x_1n₂;x₂₁, ..., x_2n₂). In order to send theis codeword over channel s₂, terminal 1 must put in the successive symbols x₁₁, ..., x_1n₂ and terminal 2 must send the successive symbols x₂₁, ..., x_2n₂. First however terminal 1 must instruct terminal 2 which sequence to send. Since M₁ ≥ a^n₂₂ there exists a one-to-one mapping from the set of all input sequences of length n₂ at terminal 2 into the set of codewords of the fist code. Suppose this mapping associates with the particular sequence \strikeout off\uuline off\uwave offx₂₁, ..., x_2n₂ during the next sequence of n₂ channel operaitions, terminal 1 fist sends the j-th codeword of the first code over channel s₁. A chane sequece (y₂₁, ..., y_2n₁) is received at termina 2 and is decoded to message i , say, using the decoding sets of the first code. Suppose the above mapping associates the i-th codeword of the first code with the input sequence (x₂₁’, ..., x_2n₂’) at terminal 2. Then, during the next n₂ channel opеrations terminal 1 send the sequence (x₁₁, ..., x_1n₂) and terminal 2 transmits simultaneously the sequence (x₂₁’, ...x_2n₂’). A chance sequence (y₃₁,..,y_3n₂) is received at terminal 3 and is decoded into message k, say, using the decoding sets of the second code. Terminal 3 concludes that message k , was originally intended by terminal 1. The total probability of an error in decoding is bounded by 2λ₀ = λ. this proves the theorem for n of the form n₁ + n₂, where n₁ and n₂ are chosen so that 52↑ and 53↑ are satisfied. For general n we can easily reduce to the case above.

9 Three-terminal channels with symmetric structure

There are channels wich have a special symetric structure which permits terminal 1 and terminal 2 to transmit independently and simultaneously over the channel. In this case, if terminla 1 first sends his message to terminal 2 who then sends the received information on to terminal 3, terminal 1 can keep sending new message during the same time as terminal 2 sends the previous ones on to terminal 3. Thus, after wasting the initial n letters by sending the first message to termina 2, no further delay is caused in sending from terminal 1 to terminal 3. For an important class of channels this procedure leads to a new bound

\mathchoiceR₅ = min(C₁(1, 2), C₁(2, 3))R₅ = min(C₁(1, 2), C₁(2, 3))R₅ = min(C₁(1, 2), C₁(2, 3))R₅ = min(C₁(1, 2), C₁(2, 3))

which is an improvement over R₂.

We first prove the following theorem:

Theorem 9.1

suppose a d.m. three-terminal channel P(y₁y₂y₃|x₁x₂x₃) satisfies the following conditions:

(i) C₁(1, 3) = 0

(ii) \strikeout off\uuline off\uwave offP(y₂y₃|x₁x₂x₃) = P(y₂|x₁x₂x₃)P(y₃|x₁x₂x₃) for all x₁, x₂, x₃, y₂ and y₃ .

(iii) There exists an input letter x₃₀ and function g₂:A₂xB₂ → A₂, such that the d.m.c K(y₃₂|x₁₁|g₂, x₃₀) with inputs x₁₁ and outputs y₃₂ defined by

(54) K(y₃₂|x₁₁|g₂, x₃₀) = ⎲⎳_y₂₁P(y₃₂|x₁₂, g(x₂₁, y₂₁), x₃₀)⋅P(y₂₁|x₁₁x₂₁x₃₀)

Мене ми изгледа дека P(y₂₁|x₁₁x₂₁x₃₀) = 1 зошто имаш ∑_y₂₁. Слични претпоставки имам во главното изведување подолу. Ако загледаш подобро изглда како усреднување по \strikeout off\uuline off\uwave offP(y₂₁|x₁₁x₂₁x₃₀) . \uuline default\uwave defaultСепак многу добро се уклопува во изведувањето подолу и мора да има некој сличен резон.

does not depend on x₂₁. Then

(55) \mathchoiceC(1, 3) ≥ C{K(y₃₂|x₁₁|g₂, x₃₀)}C(1, 3) ≥ C{K(y₃₂|x₁₁|g₂, x₃₀)}C(1, 3) ≥ C{K(y₃₂|x₁₁|g₂, x₃₀)}C(1, 3) ≥ C{K(y₃₂|x₁₁|g₂, x₃₀)}

where \strikeout off\uuline off\uwave offC{K(y₃₂|x₁₁|g₂, x₃₀)} is capacity of channel K(y₃₂|x₁₁|g₂, x₃₀).

Proof. For each n ≥ 2 we construct a channel Pⁿ(Y₃|X₁|F₂, F₃) by specifying F₂ and F₃ as follows. In 25↑ let

F₂ = {x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})}

\strikeout off\uuline off\uwave off (ова е неуспешен обид)

\strikeout off\uuline off\uwave off

Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃)

Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ⁿ∏_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1});f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1}); f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

\strikeout off\uuline off\uwave off

Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}); f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1});f^k − 1₃(x₃₁, ..., x_{3, k − 1};y₃₁, ..., y_{3, k − 1})}

\strikeout off\uuline off\uwave off

P²(Y₃|F₁|F₂, F₃) = ⎲⎳_{y₂₁, y₂₂}P(y₂₁, y₃₁|x₁₁, x₂₀, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, f¹₂(y₂₁), x^’₃₀)

(ова е неуспешен обид)

\strikeout off\uuline off\uwave off

Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ⎲⎳_Y₂Pⁿ(Y₂Y₃|F₁F₂F₃) = = ⎲⎳_Y₂ⁿ∏_k = 1P{y_2k, y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1}), (x₃₀, ..x₃₀)} = ⁿ∏_k = 1P{y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1}), (x₃₀, ..x₃₀)} = (y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2P{y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}), (x₃₀, ..x₃₀)}

\strikeout off\uuline off\uwave off

1 Pⁿ(Y₃|F₁|F₂F₃) = ⎲⎳_Y₁Y₂Pⁿ(Y₁Y₂Y₃|F₁F₂F₃) = ⎲⎳_Y₂Pⁿ(Y₂Y₃|F₁F₂F₃) = = ⎲⎳_Y₂ⁿ∏_k = 1P{y_2k, y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₂(x₂₁, ..., x_{2, k − 1};y₂₁, ..., y_{2, k − 1}), (x₃₀, ..x₃₀)} = = ⎲⎳_Y₂(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2P{y_2k, y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}), (x₃₀, ..x₃₀)} = ⎲⎳_Y₂ⁿ∏_k = 2P{y_2k|(x₁₁, ..., x_1k − 1), f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}), (x₃₀, ..x₃₀)}⋅P{y_3k|(x₁₁, ..., x_1k − 1), f^k − 1₁(x₁₁, ..., x_{1, k − 1};y₁₁, ..., y_{1, k − 1}), (x₃₀, ..x₃₀)}

where x₂₁ is chosen arbitrary but fixed, and let F₃ = {x₃₀, ..., x₃₀}. With this choice of F₂ and F₃, and for all X₁ = (x₁₁, ..., x_1n) and Y₃ = (y₃₁, ..., y_3n)

(56) \mathchoicePⁿ(Y₃|X₁|F₂, F₃) = P(y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2⎲⎳_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀)Pⁿ(Y₃|X₁|F₂, F₃) = P(y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2⎲⎳_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀)Pⁿ(Y₃|X₁|F₂, F₃) = P(y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2⎲⎳_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀)Pⁿ(Y₃|X₁|F₂, F₃) = P(y₃₁|x₁₁, x₂₁, x₃₀)⋅ⁿ∏_k = 2⎲⎳_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀)

(MMV!!! Oвде дефинитивно е докажан изразот 56↑!!!)

Да видам што се добива за k = 2:
Pⁿ(Y₃|X₁|F₂, F₃) = P(y₃₁|x₁₁, x₂₁, x₃₀)∏ⁿ_k = 2∑_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀) =
= P(y₃₁|x₁₁, x₂₁, x₃₀)∑_{y_2, 1}P(y₃₂|x₁₂, g₂(x_2, 1, y_2, 1), x₃₀)⋅P(y_2, 1|x_1, 1, g₂(x_2, 0, y_2, 0), x₃₀) =
\mathchoice = P(y₃₁|x₁₁, x₂₁, x₃₀)∑_{y_2, 1}P(y₃₂|x₁₂, g₂(x_2, 1, y_2, 1), x₃₀)⋅P(y_2, 1|x_1, 1, x₂₁, x₃₀) = P(y₃₁|x₁₁, x₂₁, x₃₀)∑_{y_2, 1}P(y₃₂|x₁₂, g₂(x_2, 1, y_2, 1), x₃₀)⋅P(y_2, 1|x_1, 1, x₂₁, x₃₀) = P(y₃₁|x₁₁, x₂₁, x₃₀)∑_{y_2, 1}P(y₃₂|x₁₂, g₂(x_2, 1, y_2, 1), x₃₀)⋅P(y_2, 1|x_1, 1, x₂₁, x₃₀) = P(y₃₁|x₁₁, x₂₁, x₃₀)∑_{y_2, 1}P(y₃₂|x₁₂, g₂(x_2, 1, y_2, 1), x₃₀)⋅P(y_2, 1|x_1, 1, x₂₁, x₃₀)
Да видам што се добива за k = 3:

Pⁿ(Y₃|X₁|F₂, F₃) = = P(y₃₁|x₁₁, x₂₁, x₃₀)ⁿ∏_k = 2⎲⎳_{y_{2, k − 1}}P(y_3k|x_1k, g₂(x_{2, k − 1}, y_{2, k − 1}), x₃₀)⋅P(y_{2, k − 1}|x_{1, k − 1}, g₂(x_{2, k − 2}, y_{2, k − 2}), x₃₀) =

Претпоставувам исто се добива и со:

\mathchoiceX₁ = (x₁₁, ..., x_1n), F₂ = {x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})}, F₃ = {x₃₀, ..., x₃₀}X₁ = (x₁₁, ..., x_1n), F₂ = {x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})}, F₃ = {x₃₀, ..., x₃₀}X₁ = (x₁₁, ..., x_1n), F₂ = {x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})}, F₃ = {x₃₀, ..., x₃₀}X₁ = (x₁₁, ..., x_1n), F₂ = {x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})}, F₃ = {x₃₀, ..., x₃₀}

\strikeout off\uuline off\uwave off

\mathchoicePⁿ(Y₃|X₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|X₁;{x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})};{x₃₀, ..., x₃₀}}Pⁿ(Y₃|X₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|X₁;{x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})};{x₃₀, ..., x₃₀}}Pⁿ(Y₃|X₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|X₁;{x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})};{x₃₀, ..., x₃₀}}Pⁿ(Y₃|X₁|F₂F₃) = ⎲⎳_Y₁Y₂ⁿ∏_k = 1P{y_1ky_2k, y_3k|X₁;{x₂₁, g₂(x₂₁, y₂₁), ..., g₂(x_{2, n − 1}, y_{2, n − 1})};{x₃₀, ..., x₃₀}}

n = 2

P²(Y₃|F₁|F₂, F₃) = ⎲⎳_Y₂\mathchoiceP(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀) = ⎲⎳_Y₂\mathchoiceP(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₁|x₁₁, x₂₁, x₃₀)P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₁|x₁₁, x₂₁, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀) = P(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_{y₂₁y₂₂}P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀) = P(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_y₂₁P(y₂₁|x₁₁, x₂₁, x₃₀)⋅⎲⎳_y₂₂P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀) = \mathchoiceP(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_y₂₁P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)P(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_y₂₁P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)P(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_y₂₁P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)P(y₃₁|x₁₁, x₂₁, x₃₀)⎲⎳_y₂₁P(y₂₁|x₁₁, x₂₁, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)

Значи на двата начини се добива истиот резултат. Претпоставувам дека 56↑ е само посебна форма од 36↑ .

n = 3

P(y₃₁|x₁₁, x₂₁, x₃₀)⋅⎲⎳_{y₂₁y₂₂y₂₃} \oversetfor k = 1P(y₂₁|x₁₁, x₂₁, x₃₀)⋅\oversetfor k = 2P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅\overset for k = 3P(y₂₃, y₃₃|x₁₂₃, g₂(x₂₂, y₂₂), x₃₀) =

\strikeout off\uuline off\uwave off

P²(Y₃|F₁|F₂, F₃) = ⎲⎳_{y₂₁y₂₂y₂₃}P(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅P(y₂₃, y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀) =

\strikeout off\uuline off\uwave off

⎲⎳_{y₂₁y₂₂}P(y₂₁, y₃₁|x₁₁, x₂₁, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅⎲⎳_y₂₃P(y₂₃, y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀) =

⎲⎳_{y₂₁y₂₂}P(y₂₁, y₃₁|x₁₁, x₁₂, x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅P(y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀) =

⎲⎳_y₂₁P(y₂₁, y₃₁|x₁₁, x₁₂, x₃₀)⋅⎲⎳_y₂₂[P(y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀)⋅P(y₂₂, y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)] =

⎲⎳_y₂₁P(y₂₁, y₃₁|x₁₁, x₁₂, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅⎲⎳_y₂₂P(y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀) =

⎲⎳_y₂₁\cancelto1P(y₂₁|x₁₁, x₁₂, x₃₀)⋅P(y₃₁|x₁₁, x₁₂, x₃₀)⋅P(y₃₂|x₁₂, g₂(x₂₁, y₂₁), x₃₀)⋅⎲⎳_y₂₂P(y₃₃|x₁₃, g₂(x₂₂, y₂₂), x₃₀) =

Значи и за k = 2 (магента) и за k = 3 (цијан) добив дека всушност изразите добиени со36↑ и 56↑ се еквивалентни што значи дека изразот 36↑ за условите од теорема 9.1 може да се сведе на изразот 56↑.

(For k = 2 , g₂(x_{2, k − 2}, y_{2, k − 2}) = x₂₁.) Since P(y₃₁|x₁₁, x₂₁, x₃₀) does not depend on x₁₁ (заради тоа што C(1, 3) = 0) the capacity of channel Pⁿ(Y₃|X₁|F₂F₃) is equal to \mathchoice(n − 1)C{K(y₃₂|x₁₁|g₂, x₃₀)}(n − 1)C{K(y₃₂|x₁₁|g₂, x₃₀)}(n − 1)C{K(y₃₂|x₁₁|g₂, x₃₀)}(n − 1)C{K(y₃₂|x₁₁|g₂, x₃₀)} Претпоставувам дека ова лесно ќе се докаже ако се напише преносната матрица. Затоа што мислам дека е очигледно го оставам за понатаму. by theorem of [3] (оваа теорема вели дека за проширување со должина n капацитетот е nC) .

Hence

(57) (C_n(1, 3))/(n) ≥ (n − 1)/(n)⋅C{K(y₃₂|x₁₁|g₂, x₃₀)}

Овде се работи за C_n затоа што имаш Pⁿ(...) каде Y₃ и X₁ се случајни процеси.

And letting n tend to infinity (32↑)

(58) C(1, 3) ≥ C{K(y₃₂|x₁₁|g₂, x₃₀)}

This completes the proof of the theorem.

Examples.

Examples 1 and 2 of Section 3 clearly satisfy the conditions of Theorem 9.1 In Example 1 chose x₃₀ arbitrary and definite g₂ by g₂(y₂) = y₂ for all y₂. Then the channel probabilities

K(y₃₂|x₁₁|g₂, x₃₀) = ⎲⎳_y₂₁P(y₃₂|x₁₂, g₂(y₂₁), x₃₀)⋅P(y₂₁|x₁₁)

are independent of x₂₁ and constitute together a noisles binary channel with capacity equal to one. Thus C(1, 3) = C{K(y₃₂|x₁₁|g₂, x₃₀)} = 1. also, in this particular example, one has C_n(1, 3) = n − 1 for all n ≥ 1, and thus C(1, 3) = C₂(1, 3). In Example 2 choose x₃₀ = 0 and define g₂ by g₂(x₂, y₂) = x₂ + y₂(\mod2). Then channel probabilities

K(y₃₂|x₁₁|g₂, x₃₀) = ⎲⎳_y₂₁P(y₃₂|x₁₂, g(x₂₁, y₂₁), x₃₀)⋅P(y₂₁|x₁₁x₂₁)

are again independent of x₂₁ не ми изгледа така? Тоа е согласно условите на Theorem 9.1. and consitute a noisless binary channel with capacity equal to one. Thus, also in Example 2,

C(1, 3) = C{K(y₃₂|x₁₁|g₂, x₃₀)} = 1

A given channel satisfies condition (iii) of Theorem 9.1 if for every input x₃ the various matrices {P(y₂|x₁|x₂|x₃)} can be obtained from each other, for different x₂, by permutions of the columns. That is, whenever any pair of input letters x₂ is interchanged there exists a corresponding relabeling of the output letters y₂ which leaves the set of probabilitiies P(y₂|x₁|x₂|x₃) the same, for each x₃ fixed. If such a symmmetry exists in the channel, then choose x₂₀ and x₃₀ arbitrarily and let g₂(x₂₀, y₂) be any function form B₂ into A₂. For and x₂ different from x₂₀ weh obtain g₂(x₂, y₂) by fist applying the permutation h_x₂(y₂) which carries P(y₂|x₁|x₂₀|x₃₀) over into P(y₂|x₁|x₂|x₃₀) to the y₂ in g₂(x₂₀, y₂) thus g₂(x₂, y₂) = g₂(x₂₀, h_x(y₂)). Using this function g₂ the set of conditional probabilities K(y₃₂|x₁₁|g₂, x₃₀) does not depend on x₂₁. In order to get rid of the dependence of y₂ on x₃ we assume for convinience also that \mathchoiceC₁(3, 2) = 0C₁(3, 2) = 0C₁(3, 2) = 0C₁(3, 2) = 0. We now have

Theorem 9.2

\strikeout off\uuline off\uwave offSuppose a d.m. three-terminal channel P(y₁, y₂, y₃|x₁, x₂, x₃) satisfies the follownig conditions:

(i) C₁(1, 3) = C₁(3, 2) = 0

(ii) \strikeout off\uuline off\uwave offP(y₂y₃|x₁x₂x₃) = P(y₂|x₁x₂x₃)P(y₃|x₁x₂x₃) for all x₁, x₂, x₃, y₂ and y₃ .

(iii) For every pair of input letters x₂ which is interchanged there exists a permutation of the output letters y₂ which leaves the set of conditional probabilities P(y₂|x₁|x₂) unchanged.

(59) \mathchoiceC(1, 3) ≥ R₅ = min(C₁(1, 2), C₁(2, 3))C(1, 3) ≥ R₅ = min(C₁(1, 2), C₁(2, 3))C(1, 3) ≥ R₅ = min(C₁(1, 2), C₁(2, 3))C(1, 3) ≥ R₅ = min(C₁(1, 2), C₁(2, 3))

Proof. Since C(1, 3) = C₁(3, 2) = 0 we may write \mathchoiceP(y₂, y₃|x₁x₂x₃) = P(y₂|x₁x₂)⋅P(y₃|x₂x₃)P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁x₂)⋅P(y₃|x₂x₃)P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁x₂)⋅P(y₃|x₂x₃)P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁x₂)⋅P(y₃|x₂x₃). For each x₂ the capacity of channel P(y₂|x₁|x₂) is equal to C₁(1, 2), by condition (iii). Chose x₂₀ arbitrary but fixed. Let x₃₀ be such that the d.m.c. P(y₃|x₂|x₃₀) has capacity C₁(2, 3). Let X₂₀ = (x₂₀, ..., x₂₀) and X₃ = (x₃₀, .., x₃₀). Let 0 ≤ λ ≤ 1, be arbitrary and λ₀ = (λ)/(2). Select n sufficiently large such that there exists a code (n, M, λ₀) for channel P(y₂|x₁|x₂₀) and such that there exists a code (n, M, λ₀) for channel P(y₃|x₂|x₃₀) both wiht rate close to R₅. We then have M distinct codewords at terminal 1; X₁(1), ..., X₁(M);X₁(m) ∈ Aⁿ₁; and M disjoint decoding subsets D₂(1), ...D₂(M) at terminal 2; D₂(m) ⊂ Bⁿ₂. Similarly we have M distinct codewors at terminal 2; X₂(1), ...X₂(M); X₂(m) ∈ Aⁿ₂; and M disjoint decoding subsets D₃(1), ..., D₃(M) at terminal 3; D₃(m) ⊂ Bⁿ₃. The probability of an error in decoding is for each code bounded by λ₀. For all X₁ = (x₁₁, ..., x_1n), X₂ = (x₂₁, ..., x_2n) \strikeout off\uuline off\uwave offY₂ = (y₂₁, ..., y_2n) and Y₃ = (y₃₁, ..., y_3n) let:

Pⁿ(Y₂|X₁X₂) = ⁿ∏_k = 1P(y_2k|x_1k, x_2k) Pⁿ(Y₃|X₂X₃) = ⁿ∏_k = 1P(y_3k|x_12k, x_3k)

Observe that condition (iii) also implies that if X₂₀ is interchanged with any other sequence X₂ = (x₂₁, ..., x_2n) then there exists a premutation h_x₂ of the output sequence Y₂ = (y₂₁, ..., y_2n) which carries the set of probabilities Pⁿ(Y₂|X₁|X₂₀) into the set of probabilities Pⁿ(Y₂|X₁|X₂). Thus for each X₂ and Y₂, there exist h_X₂(Y₂) such:

Pⁿ(h_X₂(Y₂)|X₁X₂) = Pⁿ(Y₂|X₁X₂)

for all X₁. Now define a funciton g₂:Aⁿ₂xBⁿ₂ → Aⁿ₂ by

g₂(X₂Y₂) = X₂(m) if

h_X₂(Y₂) ∈ D₂(m), m = 1, ...M.

Define the d.m.c Kⁿ(Y₃|X₁|g₂, X₃₀) with inputs X₁ and outputs Y₃ by

(60) Kⁿ(Y₃|X₁|g₂, X₃₀) = ⎲⎳_Y₂Pⁿ(Y₃|g₂(X₂, Y₂), X₃₀)⋅Pⁿ(Y₂|X₁X₂)

Clearly

(61) Kⁿ(Y₃|X₁|g₂, X₃₀) = ⎲⎳_Y₂Pⁿ(Y₃|g₂(X₂, Y₂), X₃₀)⋅Pⁿ(Y₂|X₁\mathchoiceX₂₀X₂₀X₂₀X₂₀)

for all X₂ and thus the channel is independent of X₂. Therefore the d.m. three-terminal channel Pⁿ(Y₁, Y₂, Y₃|X₁X₂X₃) satisfies the conditions of Theorem 9.1. For n sufficienlty large the system {X₁(m), D₃(m);m = 1, ..., M} forms a code (1, M, λ) for channel Kⁿ(Y₃|X₁|g₂, X₃₀). Thus for ϵ > 0 and n sufficiently large

(62) C{Kⁿ(Y₃|X₁|g₂, X₃₀)} ≥ n(R₅ − ϵ)

Applying Theorem 9.1 to cha\strikeout off\uuline off\uwave offPⁿ(Y₁, Y₂, Y₃|X₁X₂X₃) we obtain

C(1, 3) ≥ R₅

which completes the proof of the theorem.

Examples

Examples 1 and 2 of Section 3 clearly stisfy the conditions of theorem 9.2. Thus again for bot examples C(1, 3) = min(C₁(1, 2), C₁(2, 3)) = 1. Another example fo the same type is the channel with transition probabilities as follows. Al inputs and outputs are binary. Let P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁, x₂)⋅P(y₃|x₂x₃) for all x₁, x₂, x₃, y₂ adn y₃. If x₂ = 0, the channel P(y₂|x₁|x₂) is binary symettric channel wiht probability of error p, say. If x₂ = 1, the channel P(y₂|x₁|x₂) is b.s.c. with probability of error 1 − p. Thus

P(y₂ = 1|x₁ = 0, x₂ = 0) = P(y₂ = 0|x₁ = 1, x₂ = 0) = P(y₂ = 0|x₁ = 0, x₂ = 1) = P(y₂ = 1|x₁ = 1, x₂ = 1) = p

For all x₃ the channel P(y₃|x₂|x₃) is b.s.c with probabilty of error s, say. If we interchange the input letters x₂ and simultaneously interchange the output letters y₂ the channel P(Y₂|X₁|X₂) remains unaltered. Accoriding to the analysis of Theorem 9.2, \mathchoiceC(1, 3) ≥ min(1 − H(p), 1 − H(s))C(1, 3) ≥ min(1 − H(p), 1 − H(s))C(1, 3) ≥ min(1 − H(p), 1 − H(s))C(1, 3) ≥ min(1 − H(p), 1 − H(s)) where H(p) = − p⋅log₂(p) − (1 − p)⋅log₂(1 − p). In Section 10 it is shown that the capacity of this channel is in fact equal to min(1 − H(p), 1 − H(s)).

10 Upper bounds on the capacity

In this section it is shown that C₁[1, (2, 3)] and C₁[(1, 2), 3] are both an upper bound on the capacity C₁(1, 3). If the structure of a particular channel is such that one of these upper bounds coincides with one of the lower bounds, then the capacity of that channel is equal to this common value. This is the case if the channel has sufficient symetric structure. This result yields an important class of channels for which the capacity C(1, 3) can be determined with relative ease. If we define

(63) U = min{C₁[1, (2, 3)], C₁[(1, 2), 3]}

we have the following

Theorem 10.1

For any n a (1, 3)-code (n, M, λ) satisfies

(64) logM ≤ (n⋅U + 1)/(1 − λ)

This theorem clearly implies C(1, 3) ≤ U , i.e. , U is an upper bound on the capacity C(1, 3). In proving Theorem 10.1 let a (1, 3)-code (n, M, λ) be given for transmission over the channel from terminal 1 to terminal 3. This code is a code (1, M, λ) for some d.m.c Pⁿ(Y₃|F₁|F₂F₃) where the pair (F₂, F₃) is fixed. Let the input distribution (on strategies F₁ of length n) for this d.m.c be deined by the uniform distribution on messages (numbered from 1 to M). As usual we denote by \mathchoiceH(m) − H(m|Yⁿ₃)H(m) − H(m|Yⁿ₃)H(m) − H(m|Yⁿ₃)H(m) − H(m|Yⁿ₃) the amount of information received through the channel if this particular code and input distribution are used. We intend ot show that for all choices of F₂ and F₃

(65) H(m) − H(m|Yⁿ₃) ≤ n⋅C₁[1, (2, 3)]

(66) H(m) − H(m|Yⁿ₃) ≤ n⋅C₁[(1, 2), 3]

From this and Fano’s inequality [7] \strikeout off\uuline off\uwave offH(W|Ŵ) = H(W) − P(ϵ)log2^nR = H(W) − P(ϵ)n⋅R the desired result follows. In proving the inequlaities 65↑ and 66↑. we employ the technique of Shannon [5], i.e. we will consider the change in equivocation of message due to the next received letter at terminal 3. Let Y^k_t denote the sequence (y_t1, ..., y_tk) of k received letters at terminal t; t = 1, 2, 3; k = 1, ..., n; and let x_1k, x_2k, x_3k denote the k-th transmitted letters. also assume F₂ and F₃ are arbitrary but fixed. We first prove 65↑. Proceeding as Shannon in [5] and [6] we have:

H(m) − H(m|Yⁿ₃) ≤ H(m) − H(m|Yⁿ₂, Yⁿ₃) = ⁿ⎲⎳_k = 1{H(m|Y^k − 1₂, Y^k − 1₃) − H(m|Y^k₂, Y^k₃)}

∑²_k = 1{H(m|Y^k − 1₂, Y^k − 1₃) − H(m|Y^k₂, Y^k₃)} = H(m|Y⁰₂, Y⁰₃) − \cancelH(m|Y¹₂, Y¹₃) + \cancelH(m|Y¹₂, Y¹₃) − H(m|Y²₂, Y²₃) = H(m) − H(m|Y²₂Y²₃) = H(m) − H(m|Yⁿ₂, Yⁿ₃)
Внатрешните членови секогаш се поништуваат остануваат само првиот и последниот. Го имам негде видено но не знам каде(веројатно EIT). (MMV)

From the basic inequalitiew of information theory we also obtain:

\strikeout off\uuline off\uwave offF_t(m) = {x_t1, f¹_t(x_t1, y_t1), ..., f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})} \mathchoicex_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})x_tk = f^k − 1_t(x_t1, .., x_{t, k − 1};y_t1, ..., y_{t, k − 1})

H(y_2k, y_3k|Y^k − 1₂, Y^k − 1₃) = H[P(y_2k, y_3k|Y^k − 1₂, Y^k − 1₃)] P(y_2k, y_3k|F₂, F₃)P(y_2k, y_3k|Y^k − 1₂, Y^k − 1₃)
H(X|Y) ≥ H(X|Y, f(Y)) = H(X|f(Y))
Ова подолу во засега ми држи најмногу вода:
H(y_2k, y_3k|Y^k − 1₂, Y^k − 1₃) ≥ H(y_2k, y_3k|X^k − 1₂, Y^k − 1₂, X^k − 1₃Y^k − 1₃) = H(y_2k, y_3k|f(X^k − 1₂, Y^k − 1₂), f(X^k − 1₃Y^k − 1₃)) = H(y_2k, y_3k|x_2k, x_3k)
H(y_2k, y_3k|m, x_1k, x_2k, x_3k) ≤ H(y_2k, y_3k|m, Y^k − 1₁, Y^k − 1₂, Y^k − 1₃) ова е логично зошто x_2k = f(x₂₁...x_2k − 1;y₂₁...y_2k − 1) , со оглед на тоа што во RHS не ги знаеш x₂₁, ...x_2k − 1 логчно е таа неизвесност да биде поголема. Истото се добива ако се оди и со горниот доказ. Е сеа дали разликата е поголема тоа е под знак прашање.

This proves 66↑.

We thus showed that C₁[1, (2, 3)] and C₁[(1, 2), 3] are upper bounds on the capacity C(1, 3). We now investigate the consequences of this result for channels with symmetric structure.

(i) If a channel has sufficiently symetric structure that it satisfies the conditions of Theorem 9.2 then, by Lemmas 4.2 and 4.4, C₁(1, 2) = C₁[1, (2, 3)] and C₁(2, 3) = C₁[(1, 2), 3]. From this it follows immediately that for such a channle C(1, 3) = R₅ = U. Thus in Examples 1 and 2 of Section 3 the capacity of either channel is equal to one. The capacity of the channel in the last paragraph of Section 9 is exactly Equal to min(1 − H(p), 1 − H(s)).

(ii) If channel satisfies C₁(1, 2) = 0 and for all x₁, x₂, x₃, y₂ and y₃, P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁x₂x₃)⋅P(y₃|x₁x₂x₃) then by Lemma 4.1 C(1, 3) = C₁(1, 3) = C₁[1, (2, 3)].

(iii) If a channel satisfies C₁(2, 3) = 0, then, by Lemma 4.3 C(1, 3) = C₁(1, 3) = C₁[(1, 2), 3].

Examples of the last two types are quite trivial. In either case terminal 2 cannot help in the transmission procedure, other than transmtting the same letter each period.

For some channels the largest lower bound L = max(R₁, R₂, R₃, R₄, R₅) coincides wiht U and then the capacity of the channel is determined. Fro other channels the values of L and U are clearly different, as is the case in Examples 3, 4 and 5 of Section 3 6↑, and then the capacity C(1, 3) is still undetermined. For an important class of channels, however, which are not of the type (i), (ii), or (iii) above, it is possible to derive another upper bound smaller than U, namely

(67) U’ = (C₁[1, (2, 3)]⋅C₁[(1, 2), 3])/(C₁[1, (2, 3)] + C₁[(1, 2), 3])

This upper boudn applies to the Examples 3, 4 and 5 of Section 3 and in fact equalst the best lower bound in each case, and hence the capacity C(1, 3) for these channels is again eaual to this common value L = U’. We argue as follows. Suppose a channel is not of the type (i) above and assume also that C₁(1, 3) < C(1, 3). That is , suppose we know that the best transmission procedure for sending from terminal 1 to termina 3 must involve strategies at terminal 2, but also we know that terminal 2 cannot send to terminal 3 independently of terminal 1. Examples 3, 4 and 5 clearly satisfy these assumptions. Thus, at best, during n₁ transmission periods the input x₂ is fixed, and terminal 1 sens information to the pair to terminals 2 and 3, and during n − n₁ transmission periods terminals 1 and 2 send jointly to terminal 3. Then the change in equivocation of message at terminal 3, due to the next received letter is equal to zero for n₁ transmission periods. The only positive change in equivocation at terminla 3 is due to the n − n₁ letters received when the inputs at terminal 2 are random. That is:

(68) H(m) − H(m|Yⁿ₃) ≤ (n − n₁)⋅C₁[(1, 2), 3]

Also, the largest possible change in equivocation at terminal 3 is equal to the change in equivocation of message at terminals 2 and 3 due to the received letters y₂ and y₃ during the n₁ transmission periods terminal 1 sends information away. That is, (n − n₁)⋅C₁[(1, 2), 3] is at most equal to n₁⋅C₁[1, (2, 3)] or

H(m) − H(m|Yⁿ₃) ≤ (C₁[1, (2, 3)]⋅C₁[(1, 2), 3])/(C₁[1, (2, 3)] + C₁[(1, 2), 3])

As in Theorem 10.1, this shows that U’ is an upper bound on C(1, 3) for the particular type of channels for which „timesharing” is best. This also proves that for Example 3 of Section 3 the capacity is exactly equal to 0.5, for Example 4 C(1, 3) = 0.243 and for Example 5 C(1, 3) = 0.5.

References

[1] Ash. R B. (1965) Information Theory. Interscience , New York.

[2] Fano, R. M. (1952) (1954) Statistical theory of communication. Notes on a course given at the Massachusetts Institute of Technology

[3] Feinstein, A. (1958) Foundations of Information Theory. McGraw Hill, New York.

[4] C. E. Shannon, (1948) A mathematical theory of communication,” BeN Syst. Tech. J., vol. 27, pp. 379-423, July 1948.

[5] C. E. Shannon, (1958) Channels with side information at the transmitter. IBM J. Res. Develop. 2, 289-293.

[6] C. E. Shannon, (1958) Two way communication channels. Proc. Fourt Berkley Symp. math. Statist. and Prob, 1, 611-644

[7] J. Wolfowitz, Coding Theorems of Information Theory, New York: Springer-Verlag, Third Ed., 1964.