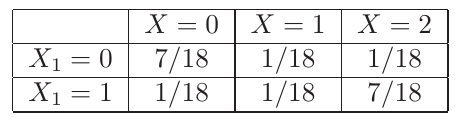Paper- T.Cover, Capacity theorem for the Relay Channels

\sloppy

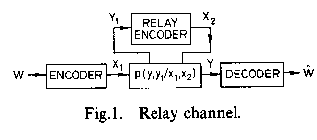
Abstract- Relay channel consist of an input x₁, a relay output y₁, a channel output y , and a relay sender x₂ (whose transmission is allowed to depend on the past symbols y₁). The dependence of the received symbols upon the inputs is given by p(y, y₁|x₁, x₂₎. The channel is assumed to be memoryless. In this paper following capacity theorems are proved.

1. If y is a degraded form of y₁, then

C = max_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y₁|X₂)}.

2. If y₁ is degraded form of y, then

C = max_p(x₁₎max_x₂{I(X₁;Y|x₂).

3. If p(y, y₁|x₁, x₂) is an arbitrary relay channel with feedback from (y, y₁) to both x₁ and x₂, then

C = max_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁; Y, Y₁|X₂)}

4. For a general relay channel

\mathchoiceC ≤ max_{p(x₁, x₂)}minI(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)C ≤ max_{p(x₁, x₂)}minI(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)C ≤ max_{p(x₁, x₂)}minI(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)C ≤ max_{p(x₁, x₂)}minI(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)

Од овој израз може да сконташ дека капацитетот на генерален рејлиев канал е аналоген на max-flow min-cut алгоритамот. Го сконтав откако ја помина вглавата 15.7 од EIT.

Во EIT книгата наместо X₂ користат X₁, а наместо X₁ користат X. Таму кпацитетот на генерален рејлиев канал е:
C ≤ sup_p(x, x₁)min{I(X, X₁;Y), I(X;Y, Y₁|X₁)}

Figure 1 Relay Channel

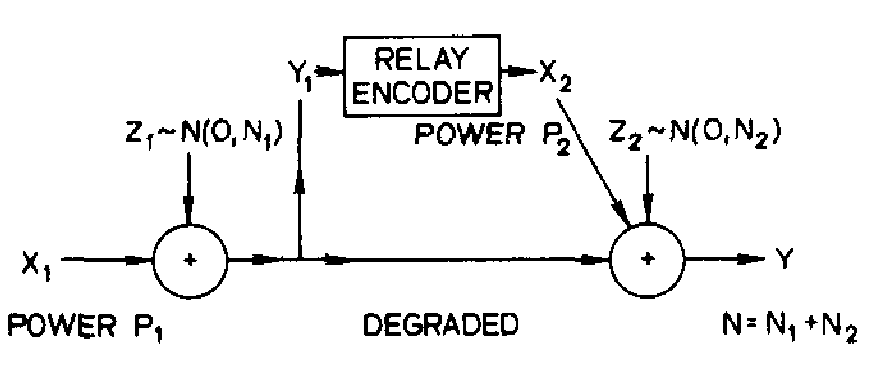
THE Discrete memoryless relay channel denoted as (X₁x X₂ , p(y, y₁|x₁, x₂), YxY₂) consist of four finite sets: X_\mathnormal1, X_\mathnormal2, Y, Y_\mathnormal1 and a collection of probability distributions p(., .|x₁, x₂) on YxY_\mathnormal1one for each (x₁, x₂) ∈ X_\mathnormal1xX_\mathnormal2. The interpretation is that x₁ is the input to the channel and y is the output, y₁ is the relay output and x₂ is the input symbol chosen by the relay as shown on 1↑. The channel is memoryless in the sense that the current received symbols (Yⁱ₂, Yⁱ₃) and the message and past symbols (m, Xⁱ⁻¹₁, Xⁱ⁻¹₂, Yⁱ⁻¹₂, Yⁱ⁻¹₃) are conditionally independent given the current transmitted symbols (Xⁱ₁, Xⁱ₂). The problem is to find the capacity of the channel between the sender x₁ and the receiver y. The model that motivates our investigation of degraded relay channels is perhaps best illustrated in the Gaussian case (4↓). Suppose the transmitter x₁ has power P₁ and the relay transmitter has power P₂. The relay receiver \mathchoicey₁y₁y₁y₁ sees \mathchoicex₁ + z₁x₁ + z₁x₁ + z₁x₁ + z₁, z₁ = N(0, N₁). The intended receiver y sees the sum of the relay signal x₂ and a corrupted version of y₁, i.e., y = x₂ + y₁ + z₂ z₂ ~ N(0, N₂). How should x₂ use his knowledge of x₁ (obtained through y₁) to help y understand x₁?

Figure 2 Ternary relay channel

За да сватиш зошто се вакви ознаките треба да го видиш чланакот од van der Meulen

We shell show that capacity is given with

C^* = max_{0 ≤ α ≤ 1}min⎧⎩C⎛⎝⎛⎝(P₁ + P₂ + 2√( α⋅P₁P₂))/(N₁ + N₂)⎞⎠, C⎛⎝(αP)/(N₁)⎞⎠⎞⎠⎫⎭

where C(x) = (1)/(2)log(1 + x). An interpretation consistent with achieving C^* in this example is that y₁ discovers x₁ perfectly, then x₂ and x₁ cooperate coherently in the next block to resolve the remaining y uncertainty about x₁. Многу убаво кажано H(x₁|y) неизвесност колку добро го знаеш x₁ ако го знеш y However, in this next block, fresh x₁ information is superimposed, thus resulting in a steady-state resolution of the past uncertainty and infusion of new information.

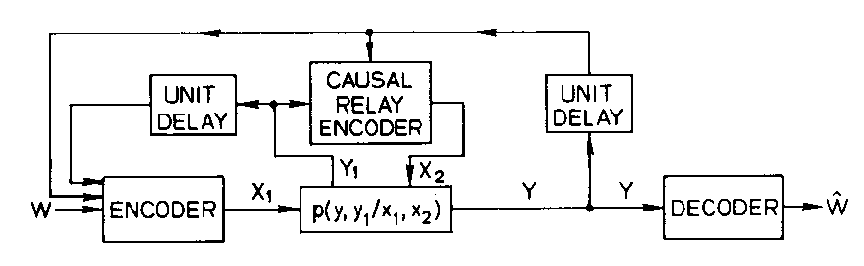
An (M, n) code for the relay channel consist of a set of integers:

(1) \mathnormalW = {\mathnormal\mathnormal1, 2, ..., M}\overset△ = \mathnormal\mathnormal[\mathnormal\mathnormal1, M]

an encoding function

(2) x₁: W → X^\mathnormaln_\mathnormal1

a set of relay functions {f_i}ⁿ_i = 1 such that:

(3) x_2i = f_i(Y₁₁, Y₁₂, …, Y_{1 i − 1}), 1 ≤ i ≤ n

Дефиницијата на симболот што се испраќа одговара на дефиницијата на стратегиите во релето во чланакот од van der Meulen. Со други зборови овде сака да каже дека сигналот што го испраќа релето во i-от тајмслот зависи од (i − 1)-те претходно примените сигнали во релето.

and a decoding function

(4) g: Yⁿ → W

For generality, the encoding functions x₁(⋅), f_i(⋅) and decoding function g(⋅) are allowed to be stochastic functions.

Note that the allowed relay encoding functions actually form part of the definition o the relay channel because of the non-anticipatory relay condition. The relay channel input x_2i is allowed to depend only on the past \mathchoiceyⁱ₁ = (y₁₁, y_i1, …, y_{1 i − 1})yⁱ₁ = (y₁₁, y_i1, …, y_{1 i − 1})yⁱ₁ = (y₁₁, y_i1, …, y_{1 i − 1})yⁱ₁ = (y₁₁, y_i1, …, y_{1 i − 1}). The channel is memory-less in the sense that (y_i, y_{1 i}) depends on the past (xⁱ₁, xⁱ₂) only through the current transmitted symbols (x_{1 i}, x_{2 i}). Thus, for any choice p(w), w ∈ M, and code choice x₁: W → X^\mathnormaln_\mathnormal1 and relay functions {f_i}ⁿ_i = 1, the joint probability mass function on W\mathnormalxX^\mathnormaln_\mathnormal1\mathnormalxX^\mathnormaln_\mathnormal2\mathnormalxY^\mathnormaln\mathnormalxY^\mathnormaln_\mathnormal1 is given by:

If the message w ∈ W is sent, let

(6) λ(w) = Pr{g(Y) ≠ w}

Потсетување од EIT на Cover

λ(w) = Pr(g(Yⁿ) ≠ w|Xⁿ = xⁿ(w)) = ⎲⎳_yⁿP(yⁿ|xⁿ(w))⋅I(g(yⁿ) ≠ w)

denote the conditional probability of error. We define the average probability of error of the code to be:

(7) P_n(e) = (1)/(M) ⎲⎳_wλ(w)

The probability of error is calculated under a special distribution - uniform distribution over the codewords w ∈ [1, M]. Finally let:

λ_n = max_w ∈ W{λ(w)}

be the maximal probability of error for the (M, n) code.

The rate R of an (M, n) code is defined by:

(8) R = (1)/(n)⋅log(M) bits/transmission

The rate R is said to be achievable by a relay channel if, for any ϵ > 0 and for all n sufficiently large, there exist an (M, n)code with

(9) \mathchoiceM ≥ 2^nRM ≥ 2^nRM ≥ 2^nRM ≥ 2^nR

R − ϵ ≤ (1)/(n)⋅log(M); n⋅(R − ϵ) ≤ log(M); 2^{n⋅(R − ϵ)} ≤ M

such as that λ_n ≤ ϵ. The capacity C of the relay channel is the supremum of the set of achievable rates.

мое прво резонирање:

log(M) ≥ nR; R ≤ (1)/(n)⋅log(M)

(This is bit different definition of achievability compared to the definition in the T. Cover textbook.)

Кога го преведував за докторатот, ми стана логичен на крај изразот 9↑. Се сетив на noisy typewriter. Таму дактилографката ја греши секоја втора буква. M = 28 а R = log(14)

M ≥ 2^log(14) = 14. Значи ако имаш безгрешна дактилографка тогаш M = 28 = 2^log(|X|) = 2^log(28).

We now consider a family of relay channels in which the relay receiver y₁ is better than the ultimate receiver y in the sense defined below.

The relay channel (X_\mathnormal1xX_\mathnormal2, \mathnormalp(y, y₁|x₁, x₂), YxY_\mathnormal1) is said to be degraded if p(y, y₁|x₁, x₂) can be written in the form

Equivalently, we see by inspection of 10↑ that a relay channel is degraded if p(y|x₁, x₂, y₁) = p(y|x₂, y₁) i.e., \mathchoiceX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → Y form Markov chain .

The previously discussed Gaussian channel is therefore degraded. For the reader familiar with the definition of the degraded broadcast channel, we observe that a degraded relay channel can be looked at as a family of physically degraded broadcast channels indexed by x₂. A weaker form of degradation (stochastic) can be defined for relay channels, but Theorem 1 below then becomes only an inner bound to the capacity. The case in which the relay y₁ is worse than y is less interesting (except for the converse) and is defined as follows. Сака да каже дека во нормални услови сигналот во релето y₁ е подобар од сигналот во приемникот. За обратно деградиран канал сигналот во приемникот е подобар од сигналот во релето.

The relay channel (X_\mathnormal1xX_\mathnormal2, \mathnormalp(y, y₁|x₁, x₂), YxY_\mathnormal1) is reversely degraded if p(y, y₁|x₁, x₂) can be written in following form

The main contribution of this paper is summarized by the following three theorems.

The capacity C of the degraded relay channel is given

(12) C = sup_p(x1, x2)min{I(X₁, X₂;Y), I(X₁;Y₁|X₂)}

where supremum is over all joint distributions p(x₁, x₂) on (X_\mathnormal1, X_\mathnormal2).

The capacity C₀ of the reversely degraded relay channel is given by

(13) C₀ = max_{x₂ ∈ X₂}max_p(x₁)I(X₁;Y|x₂).

Theorem 2 has a simple interpretation. Since the relay y₁ sees a corrupted version of what y sees, x₂ can contribute no new information to y - thus x₂ is set constantly at the symbol that „opens“ the channel for the transmission of x₁ directly to y at rate I(X₁;Y|x₂). The converse proves that one can do no better.

Theorem 1 has a more interesting interpretation. The first term in the brackets in 12↑ sugest that a rate I(X₁, X₂;Y) can be achieved where p(x₁, x₂) is arbitrary. However, this rate can only be achieved by complete cooperation of x₁ and x₂. To set up this cooperation x₂ must know x₁. Thus the x₁ rate of transmission should be less than I(X₁;Y₁|X₂). (How they cooperate given these two conditions will be left to the proof.) Finally, both constraints lead to the minimum characterization in 12↑.

Сака да каже ако x₂ може да придонесе со нова информација на y тогаш \strikeout off\uuline off\uwave offI(X₁, X₂;Y) ≥ I(X₁;Y₁|X₂) ако не придонесува нова информација тогаш\uuline default\uwave default \strikeout off\uuline off\uwave offI(X₁, X₂;Y)=I(X₁;Y₁|X₂)

\strikeout off\uuline off\uwave offКоја е поентата тогаш да зема минимум?

18.06.14
I(X₁, X₂;Y) = \overset(*)I(X₂;Y₁) + I(X₁;Y₁|X₂) = I(X₁;Y₁) + I(X₂;Y₁|X₁); I(X₁, X₂;Y) ≥ I(X₁;Y₁|X₂)
(*) - Мислам дека овој член е 0 зошто X₂ е функција од Y₁.

The obvious notion of an arbitrary relay channel with causal feedback (from both y and y₁ to x₁ and x₂) will be formalized in Section V. The following theorem can then be proved.

The Capacity of C_FB of an arbitrary relay channel with feedback is given by:

(14) C_FB = sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}

Note that C_FB is the same as C except that Y₁ is replaced by (Y, Y₁) in I(X₁;Y₁|X₂). The reason is that the feedback changes an arbitrary relay channel into a degraded relay channel in which x₁ transmits information to x₂ by way of y₁ and y. Clearly Y is a degraded form of (Y, Y₁).

Theorem 2 is included for reasons of completeness, but it can be shown to follow from a chain of remarks in [1] under slightly stronger conditions. Specifically in [1] .

R₁ = C₁(1, 2),

\mathchoiceLema4.1.Lema4.1.Lema4.1.Lema4.1. C₁(1, 3) ≤ C₁[1, (2, 3)] with equality if both

P(y₂, y₃|x₁x₂x₃) = P(y₂|x₁, x₂, x₃)P(y₃|x₁, x₂, x₃)
(i.e., the outputs y₂ and y₃ are conditionally independent given the inputs x₁x₂ and x₃, and \mathchoiceC₁(1, 2) = 0C₁(1, 2) = 0C₁(1, 2) = 0C₁(1, 2) = 0.

\strikeout off\uuline off\uwave off\mathchoiceTheorem 10.1.Theorem 10.1.Theorem 10.1.Theorem 10.1. \uuline default\uwave defaultFor any n a (1, 3)-code (n, M, λ) satisfies

logM ≤ (n⋅U + 1)/(1 − λ)

\mathchoiceTheorem7.1.Theorem7.1.Theorem7.1.Theorem7.1.Let ϵ > 0 and 0 < λ ≤ 1 be arbitrary. For any d.m. three-terminal channel and all n sufficiently large there exists a (1, 3) -code (n, M, λ) with M > 2^{n[C(1, 3) − ϵ]}.

Figure 3 Degraded Gaussian relay channel.

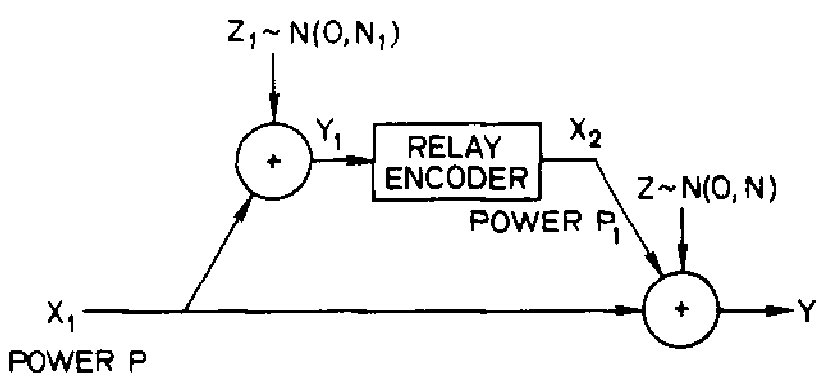
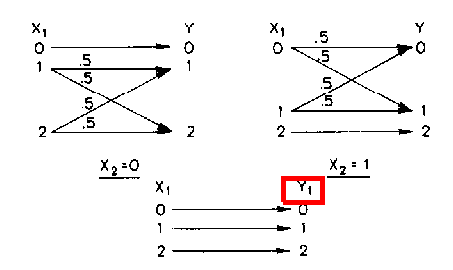
Before proving the theorems, we apply the result 12↑ to a simple example introduced by Sato [4]. The channel as shown in 2↑ has X_\mathnormal1 = Y = Y_\mathnormal1 = \mathnormal\mathnormal\mathnormal{0, 1, 2}, X_\mathnormal2 = \mathnormal{0, 1}, and the conditional probability p(y, y₁|x₁, x₂) satisfies 10↑. Specifically, the channel operation is:

(15) y₁ ≡ x₁

and

p(y|y₁, x₂ = 0) = y₁ = 0 y₁ = 1 y₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦

Sato calculated a cooperative upper bound to the channel capacity of the channel, \mathchoiceR_UG = max_{p(x₁, x₂)}I(X₁, X₂;Y) = 1.170R_UG = max_{p(x₁, x₂)}I(X₁, X₂;Y) = 1.170R_UG = max_{p(x₁, x₂)}I(X₁, X₂;Y) = 1.170R_UG = max_{p(x₁, x₂)}I(X₁, X₂;Y) = 1.170.

By restricting the relay encoding functions to

i) x_2i = f(y₁₁, ..., y_1i − 1) = f(y_1i − 1) 1 < i ≤ n, ii) x_2i = f(y₁₁, ..., y_1i − 1) = f((y_1i − 2, y_1i − 1) 1 < i ≤ n.

Sato calculated two lower bounds to the capacity of the channel:

i) R₁ = 1.0437 ii) R₂ = 1.0549

From Theorem 1 we obtain the true capacity C = 1.161878. The optimal joint distribution on X_\mathnormal1xX_\mathnormal2 is given in Table 1.

We shall see that instead of letting the encoding functions of the relay depend only on a finite number of previous y₁ transmissions, we can achieve C by allowing block Markovian dependence of x₂ and y₁ in a manner similar to [6].

Од El Gamal NIT:
Since the relay codeword transmitted in a block depends statistically on the message transmited in the previous block, we reffer to this scheme as block Markov coding (BMC)

Подолу се обидите да го добијам C = 1.161878. Го добив во последниот обид 5↓. Пресметувам само I(X₁, X₂;Y) но не и I(X₁;Y₁|X₂). Исто така сеуште не успеав да ја добијам сам оптималната дистрибуција од чланакот но ја добив 5↓ дистрибуцијата од NIT Lecture Notes Relay with limmited lookahead (која претходно ја проверував во 5↓). Тоа е таа дистрибуција од која Cover го добива R_UG = max_{p(x₁, x₂)}I(X₁, X₂;Y).

02.07.14
Сега ми текна дека дистрибуцијата од чланакот ја имаат добиено со Lagrange Multipliers. Така немам пробано. Само легитимен ми е начинот со извод и не знам зошто би пробувал на дру начин.
04.07.14
Ова од 02.07 мислам дека не треба да се проверува. C = 1.161878 се добива со рестрикција на кодирачката функција да зависи од еден претходен симбол но не и порака. Не знам како се прави сега тоа. Веројатно треба да работам со n-битни низи. Засега ќе го оставам на on-hold.
Не, не, не!!! C = 1.161878 е true capacity изгледа треба да го пресметам I(X₁;Y₁Y|X₂). Јас цело време се мотав пресметувајќи го I(X₁;Y₁|X₂) а тоа е за деградиран релеен канал.

C = max_{p(x₁, x₂)}I(X₁, X₂;Y); I(X₁, X₂;Y) = H(Y) − H(Y|X₁, X₂) = H(X₁, X₂) − H(X₁, X₂|Y)H(Y|X₂ = 0) = ∑_xp(x₁)⋅H(Y|X₂ = 0, X₁ = x₁) = p(X₁ = 0)⋅H(Y|X₂ = 0, X₁ = 0) + p(X₁ = 1)⋅H(Y|X₂ = 0, X₁ = 1) + p(X₁ = 2)⋅H(Y|X₂ = 0, X₁ = 2)

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₂p(x₂)⋅H(Y|X₁, X₂ = x₂) = p(X₂ = 0)⋅H(Y|X₂ = 0, X₁) + p(X₂ = 1)⋅H(Y|X₂ = 1, X₁) =

= \mathchoicep(X₂ = 0)⋅(p(X₁ = 1) + p(X₁ = 2)) + p(X₂ = 1)⋅(p(X₁ = 0) + p(X₁ = 1))p(X₂ = 0)⋅(p(X₁ = 1) + p(X₁ = 2)) + p(X₂ = 1)⋅(p(X₁ = 0) + p(X₁ = 1))p(X₂ = 0)⋅(p(X₁ = 1) + p(X₁ = 2)) + p(X₂ = 1)⋅(p(X₁ = 0) + p(X₁ = 1))p(X₂ = 0)⋅(p(X₁ = 1) + p(X₁ = 2)) + p(X₂ = 1)⋅(p(X₁ = 0) + p(X₁ = 1))

\strikeout off\uuline off\uwave offI(X₁, X₂;Y) = H(Y) − (p(X₂ = 0)⋅p(X₁ = 1) + p(X₂ = 0)⋅p(X₁ = 2) + p(X₂ = 1)⋅p(X₁ = 0) + p(X₂ = 1)⋅p(X₁ = 1))

\strikeout off\uuline off\uwave offC = log(3) − H(Y|X₁, X₂) = log(3) − (p(X₂ = 0)⋅p(X₁ = 1) + p(X₂ = 0)⋅p(X₁ = 2) + p(X₂ = 1)⋅p(X₁ = 0) + p(X₂ = 1)⋅p(X₁ = 1)) = \normalcolor1.2935825010

\strikeout off\uuline off\uwave off

Ова последново во е согласно веројатностите дадени во чланакот

\strikeout off\uuline off\uwave off x₂ = 0 x₂ = 1 \overset x₁ = 0 x₂ = 1 x₃ = 2 ⎡⎢⎣ 0.35431 0.072845 0.072845 0.072845 0.072845 0.35431 ⎤⎥⎦

\strikeout off\uuline off\uwave offp(X₂ = 0)⋅p(X₁ = 1) + p(X₂ = 0)⋅p(X₁ = 2) + p(X₂ = 1)⋅p(X₁ = 0) + p(X₂ = 1)⋅p(X₁ = 1) = p(x₂ = 0, x₁ = 1) + p(02) + p(10) + p(11) = 0.2913800000

0.072845 + 0.072845 + 0.072845 + 0.072845 = 0.29138

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₁, x₂p(x₁, x₂)⋅H(Y|X₂ = x₂, X₁ = x₁) = p(0, 0)H(Y|00) + p(01)H(Y|01) + p(0, 2)H(Y|02) + p(1, 0)H(Y|10) + p(11)H(Y|11) + p(1, 2)H(Y|12)

H(Y|00) = H(Y|X₂ = 0, X₁ = 0) = 0; H(Y|01) = 1; H(Y|02) = 1H(Y|10) = H(Y|X₂ = 1, X₁ = 0) = 1; H(Y|11) = 1; H(Y|12) = 0

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₁, x₂p(x₁, x₂)⋅H(Y|X₂ = x₂, X₁ = x₁) = 0 + 0.072845⋅1 + 0.072845⋅1 + 0.072845⋅1 + 0.072845⋅1 + 0 = 0.2913800000

log₂(3) − H(Y|X₁,X₂) = 1.585 − 0.2913800000 = 1.29362
И на овој начин пак го добивам истиот капацитет

Мојот резултат 5↑ не одговара на резултатот од чланакот. Мислам дека лошо го рачунам H(Y) !?

Дали можеби треба вака:
log₃(3) − H(Y|X₁,X₂) = 1 − 0.2913800000 = 0.70862 ternary symbols/transmission
(0.70862)/(log₃(2)) = 1.123136127 bits/transmission
x = log_m(y) m^x = y ⁄ log₂(...) x⋅log₂(m) = log₂(y) x = (log₂(y))/(log₂(m)) log_m(y) = (log₂(y))/(log₂(m))
x = log₂(y) 2^x = y ⁄ log_m(...) x⋅log_m(2) = log_m(y) x = (log_m(y))/(log_m(2)) log₂(y) = (log_m(y))/(log_m(2))

Ова е втор обид откако го поминав чланакот од van der Meulen

p(y|x₁, x₂ = 0) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦

p(y|x₁, x₂ = 1) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦

\strikeout off\uuline off\uwave offH(Y|X₁X₂) = P(X₂ = 0)⋅H(Y|X₁X₂ = 0) + P(X₂ = 1)⋅H(Y|X₁X₂ = 1) = P(X₂ = 0)[p(X₁ = 1) + p(X₁ = 2)] + P(X₂ = 1)⋅[p(X₁ = 0) + p(X₁ = 1)]

I(X₁, X₂;Y) = H(Y) − H(Y|X₁, X₂) = H(Y) − p(X₂ = 0)⋅[p(X₁ = 1) + p(X₁ = 2)] − P(X₂ = 1)⋅[p(X₁ = 0) + p(X₁ = 1)]
= H(Y) − p(X₁ = 1) − (X₂ = 0)⋅p(X₁ = 2) + P(X₂ = 1)⋅p(X₁ = 0)
log₂(3) = 1.585 − − 1 ⁄ 3 − 1 ⁄ 2⋅1 ⁄ 3 − 1 ⁄ 2⋅1 ⁄ 3 = 1.585 − (2)/(3) = 1.585 − 0.67 = 0.918 ternary symbols/transmission
(0.918)/(log₂[3]) = 0.5791 bits/transmission

\strikeout off\uuline off\uwave offI(X₁;Y₁|X₂) = H(Y₁) − H(Y₁|X₁X₂) = log₂(3) зошто x₁ ≡ y₁

I(X₁, X₂;Y) ≥ I(X₁;Y₁|X₂)
Ако одам со оптималните вредности за веројатноста од чланакот

\strikeout off\uuline off\uwave off x₂ = 0 x₂ = 1 \overset x₁ = 0 x₂ = 1 x₃ = 2 ⎡⎢⎣ 0.35431 0.072845 0.072845 0.072845 0.072845 0.35431 ⎤⎥⎦

I(X₁, X₂;Y) = H(Y) − H(Y|X₁, X₂) = H(Y) − (X₂ = 0)⋅[p(X₁ = 1) + p(X₁ = 2)] − P(X₂ = 1)⋅[p(X₁ = 0) + p(X₁ = 1)] = \mathchoiceH(Y) − p(X₂ = 0)⋅p(X₁ = 1) − p(X₂ = 0)⋅p(X₁ = 2) − p(X₂ = 1)⋅p(X₁ = 0) − p(X₂ = 1)⋅p(X₁ = 1) = H(Y) − p(X₂ = 0)⋅p(X₁ = 1) − p(X₂ = 0)⋅p(X₁ = 2) − p(X₂ = 1)⋅p(X₁ = 0) − p(X₂ = 1)⋅p(X₁ = 1) = H(Y) − p(X₂ = 0)⋅p(X₁ = 1) − p(X₂ = 0)⋅p(X₁ = 2) − p(X₂ = 1)⋅p(X₁ = 0) − p(X₂ = 1)⋅p(X₁ = 1) = H(Y) − p(X₂ = 0)⋅p(X₁ = 1) − p(X₂ = 0)⋅p(X₁ = 2) − p(X₂ = 1)⋅p(X₁ = 0) − p(X₂ = 1)⋅p(X₁ = 1) = log₂(3) − p(01) − p(02) − p(10) − p(11) = log₂(3) − 4⋅0.072845 = 0.585 − 0.2913800000 = 1.29362

p(10) + p(20) + p(01) + p(11)
Сега сакам да го пресметам H(Y) како што треба:

p(Y = 0|X₂ = 0) = p(X₁ = 0) = p₁₀; p(Y = 1|X₂ = 0) = (p(X₁ = 1))/(2) + (p(X₁ = 2))/(2) = (p₁₁)/(2) + (p₁₂)/(2); p(Y = 2|X₂ = 0) = (p₁₁)/(2) + (p₁₂)/(2) пази индексот „12“ одговара на x₁ = 2

p(Y = 0|X₂ = 1) = (p(X₁ = 0))/(2) + (p(X₁ = 1))/(2) = (p₁₀)/(2) + (p₁₁)/(2); p(Y = 1|X₂ = 1) = (p(X₁ = 0))/(2) + (p(X₁ = 1))/(2) = (p₁₀)/(2) + (p₁₁)/(2); p(Y = 2|X₂ = 1) = p(X₁ = 2) = p₁₂;
p(Y = 0) = p₂₀⋅p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠; p(Y = 1) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₂)/(2); p(Y = 2) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂
Ова во квадратчево не е добро требa да биде p₁₁.

А̀ко земам дека p₂₀ = p₂₁ = (1)/(2)

p(Y = 0) = (p₁₀)/(2) + (1)/(2)⋅⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠ = (3p₁₀)/(4) + (p₁₁)/(4); p(Y = 1) = (1)/(2)⋅(p₁₁ + p₁₂)/(2) + (1)/(2)⋅(p₁₀ + p₁₁)/(2) = (p₁₀)/(4) + (p₁₁)/(2) + (p₁₂)/(4); p(Y = 2) = (1)/(2)⋅(p₁₁ + p₁₂)/(2) + (p₁₂)/(2) = (p₁₁)/(4) + (3⋅p₁₂)/(4)
− H(Y) = p(Y = 0)⋅log(p(Y = 0)) + p(Y = 1)⋅log(p(Y = 1)) + p(Y = 2)⋅log(p(Y = 2))
H(Y) = H⎛⎝(3⋅p₁₀ + p₁₁)/(4), (p₁₀ + 2⋅p₁₁ + p₁₂)/(4), (p₁₁ + 3⋅p₁₂)/(4)⎞⎠
− H(Y) = (3⋅p₁₀ + p₁₁)/(4)⋅log⎛⎝(3⋅p₁₀ + p₁₁)/(4)⎞⎠ + (p₁₀ + 2⋅p₁₁ + p₁₂)/(4)⋅log⎛⎝(p₁₀ + 2⋅p₁₁ + p₁₂)/(4)⎞⎠ + (p₁₁ + 3⋅p₁₂)/(4)⋅log⎛⎝(p₁₁ + 3⋅p₁₂)/(4)⎞⎠

\strikeout off\uuline off\uwave offH(Y) = (3⋅p₁₀ + p₁₁)/(4)⋅log⎛⎝(3⋅p₁₀ + p₁₁)/(4)⎞⎠ + (p₁₀ + 2⋅p₁₁ + 1 − p₁₀ − p₁₁)/(4)⋅log⎛⎝(p₁₀ + 2⋅p₁₁ + 1 − p₁₀ − p₁₁)/(4)⎞⎠ + (p₁₁ + 3⋅(1 − p₁₀ − p₁₁))/(4)⋅log⎛⎝(p₁₁ + 3⋅(1 − p₁₀ − p₁₁))/(4)⎞⎠

H(Y) = (3⋅p₁₀ + p₁₁)/(4)⋅log⎛⎝(3⋅p₁₀ + p₁₁)/(4)⎞⎠ + (p₁₁ + 1)/(4)⋅log⎛⎝(p₁₁ + 1)/(4)⎞⎠ + (p₁₁ + 3 − 3p₁₀ − 3p₁₁)/(4)⋅log⎛⎝(p₁₁ + 3 − 3p₁₀ − 3p₁₁)/(4)⎞⎠
H(Y) = (3⋅p₁₀ + p₁₁)/(4)⋅log⎛⎝(3⋅p₁₀ + p₁₁)/(4)⎞⎠ + (p₁₁ + 1)/(4)⋅log⎛⎝(p₁₁ + 1)/(4)⎞⎠ + (3 − 3⋅p₁₀ − 2⋅p₁₁)/(4)⋅log⎛⎝(3 − 3⋅p₁₀ − 2⋅p₁₁)/(4)⎞⎠

Ако земам 5↑ тогаш со изводи во мапле најдов дека H(Y) = log₂(3).

Треба да се реши со произволни вредности на p₂₀, p₂₁. Го решив во maple ама пак добив дека H(Y) = log(3). Кога барав извод од изразот во магента не добивав резултат.

Треба да се реши каде p(x₁) и p(x₂) нема да ги третирам независно туку каде ќе зависат еден од друг т.е. да го претставам I(...) преку здружените веројатностиp(x₁, x₂) па потоа да вадам извод по p(x₁, x₂) .

p(y|x₁, x₂ = 0) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦

p(y|x₁, x₂ = 1) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦

p(x₂) = 0; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦ p(x₂) = 1; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₁, x₂p(x₁, x₂)⋅H(Y|X₂ = x₂, X₁ = x₁) = p(0, 0)H(Y|00) + p(10)H(Y|10) + p(20)H(Y|20) + p(01)H(Y|01) + p(11)H(Y|11) + p(2, 1)H(Y|21)

= p(00)⋅0 + \mathchoicep(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11) + p(21)⋅0 го имав p(11) пропуштено!!!

Пази на индексите овде се разликуваат од индексите кога ги пресметував условните веројатности погоре. На пример овде „20” подразбира x₁ = 2, x₂ = 0

Подолниве изрази за p(Y) се точни овие погоре немаат врска!!!
p(Y = 0) = p(X₁ = 0, X₂ = 0)⋅p(Y = 0|X₁ = 0, X₂ = 0) + p(X₁ = 0, X₂ = 1)⋅p(Y = 0|X₁ = 0, X₂ = 1) + p(X₁ = 1, X₂ = 1)⋅p(Y = 0|X₁ = 1, X₂ = 1) = \mathchoicep(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);
p(Y = 1) = \mathchoice(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2); p(Y = 2) = \mathchoice(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)
H(Y) = − ⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠
p(00) + p(10) + p(20) + p(01) + p(11) + p(21) = 1 p(00) = 1 − p(10) + p(20) + p(01) + p(11) + p(21)

\strikeout off\uuline off\uwave off\mathchoicep(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;

\strikeout off\uuline off\uwave offa + b + c + d + e + f = 1

\strikeout off\uuline off\uwave offH(Y) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠

I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − e
Можеби решението е:
\mathchoiceC = max(I(X₁, X₂;Y)) = log₂(3) − b − c − d − e = log₂(3) − 4⋅0.072845 = 1.2936C = max(I(X₁, X₂;Y)) = log₂(3) − b − c − d − e = log₂(3) − 4⋅0.072845 = 1.2936C = max(I(X₁, X₂;Y)) = log₂(3) − b − c − d − e = log₂(3) − 4⋅0.072845 = 1.2936C = max(I(X₁, X₂;Y)) = log₂(3) − b − c − d − e = log₂(3) − 4⋅0.072845 = 1.2936

\strikeout off\uuline off\uwave offC = sup_p(x1, x2)min{I(X₁, X₂;Y), I(X₁;Y₁|X₂)}

После бара минимум. Може долната граница ја диктира: \strikeout off\uuline off\uwave offI(X₁;Y₁|X₂) но како да го пресметам?

Со овој пристап и со претпоставка \mathchoiced + e = p(01) + p(11) = hd + e = p(01) + p(11) = hd + e = p(01) + p(11) = hd + e = p(01) + p(11) = h и \mathchoiceb + c = p(10) + p(20) = kb + c = p(10) + p(20) = kb + c = p(10) + p(20) = kb + c = p(10) + p(20) = k во мапле со парцијални изводи добив:
\mathchoice{a = 1 ⁄ 2 k, h = 2 ⁄ 3 − k, k = k}{a = 1 ⁄ 2 k, h = 2 ⁄ 3 − k, k = k}{a = 1 ⁄ 2 k, h = 2 ⁄ 3 − k, k = k}{a = 1 ⁄ 2 k, h = 2 ⁄ 3 − k, k = k}

\strikeout off\uuline off\uwave off x₂ = 0 x₂ = 1 \overset x₁ = 0 x₁ = 1 x₁ = 2 ⎡⎢⎣ 0.35431 0.072845 0.072845 0.072845 0.072845 0.35431 ⎤⎥⎦

\strikeout off\uuline off\uwave offp(00) = a = 0.35431 p(10) = b = 0.072845; p(20) = c = 0.072845; p(01) = d = 0.072845; p(11) = e = 0.072845; p(21) = f = 0.35431;

Ако го пресметам I(X₁, X₂;Y) за овие вредности се добива: I(X₁, X₂;Y) = 1.04256 што приближно одговара на R₁ дадено подолу.

k = 2⋅0.072845 = 0.14569 h = 2 ⁄ 3 − 0.14569 = 0.52097666666667

h = 2⋅0.072845 = 0.14569 0.14569⋅2 = 0.29138

H(Y|X₁, X₂) = p(10) + p(20) + p(01) + p(11) = b + c + d + e
{a = 1 ⁄ 3 − 1 ⁄ 2 d − 1 ⁄ 2 e, b = 2 ⁄ 3 − c − d − e, d = d}
d = 0.072845

\strikeout off\uuline off\uwave offb = 2 ⁄ 3 − 0.072845 − 0.072845 − 0.072845 = 0.44813166666667

a = (1)/(2) − (0.072845)/(2) − (0.072845)/(2) = 0.26048833333333
{a = 4 ⁄ 9 − 1 ⁄ 2 d − 1 ⁄ 2 e, b = 2 ⁄ 9 − c − d − e, d = d}
a = 4 ⁄ 9 − 0.072845 ⁄ 2 − 0.072845 ⁄ 2 = 0.37159944444444

b = 2 ⁄ 9 − 0.072845 − 0.072845 − 0.072845 = 0.0036872222222222 0.0036872222222222⋅2 = 0.0073744444444444

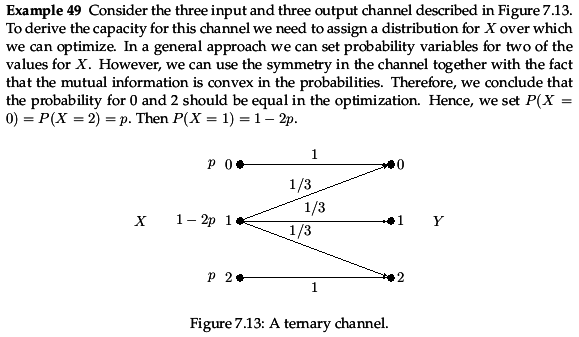
Пример за ternary channel од Lund University скриптата figure Ternary Channel Example.png

p(Y = 0) = (p + (1 − 2p)/(3)) = (1)/(3) + (p)/(3); p(Y = 1) = (1)/(3)⋅(1 − 2p) = (1)/(3) − (2p)/(3); p(Y = 2) = p + (1)/(3)⋅(1 − 2p) = (1)/(3) + (p)/(3);

H(Y) = H⎛⎝(1)/(3) + (p)/(3), (1)/(3) − (2p)/(3), (1)/(3) + (p)/(3)⎞⎠

\strikeout off\uuline off\uwave offI(X;Y) = H⎛⎝(1)/(3) + (p)/(3), (1)/(3) − (2p)/(3), (1)/(3) + (p)/(3)⎞⎠ − (1 − 2p)log₃(3)

(d)/(dx)(I(X;Y)) = 0 → p₀ = ...

После потстетувањето на проблемите од EIT 7.18 и 7.28

2^C = 2^C₁ + 2^C₂ = 2^{1 − H(p)} + 2⁰ = 3 ако p = 0 C = log₂(3) = 1.585

C = log₂(2^{1 − H(p)} + 1)

\strikeout off\uuline off\uwave off\mathchoiceC = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦C = log₂⎡⎣exp₂⎛⎝((1 − β)H_α + (α − 1)H_β)/(β − α)⎞⎠ + exp₂⎛⎝( − βH_α + αH_β)/(β − α)⎞⎠⎤⎦

\strikeout off\uuline off\uwave off⎡⎢⎣ p(y₀) p(y₁) ⎤⎥⎦ = ⎡⎢⎣ 1 0 0.5 0.5 ⎤⎥⎦⎡⎢⎣ p(x₀) p(x₁) ⎤⎥⎦

Дефинитивно се работи за канал како оној во EIT 7.28
⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦
2^C = 2^{1 − H(p)} + 2^{1 − H(q)} = 2^1 − 0 + 2^1 − 1 = 2 + 1 = 3
C = log₂(3) = 1.585
Theorem 3.3.3 од Ash не можеш да ја користиш зошто каналната матрица е сингуларна (проверив во Maple)!!!!

Се навраќам повторно на 5↑

p(y|x₁, x₂ = 0) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦

p(y|x₁, x₂ = 1) = x₁ = 0 x₁ = 1 x₁ = 2 \overset y = 0 y = 1 y = 2 ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦

p(x₂) = 0; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦ p(x₂) = 1; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦
p(y|x₁x₂) y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₁, x₂p(x₁, x₂)⋅H(Y|X₂ = x₂, X₁ = x₁) = p(0, 0)H(Y|00) + p(10)H(Y|10) + p(20)H(Y|20) + p(01)H(Y|01) + p(11)H(Y|11) + p(2, 1)H(Y|21)

= p(00)⋅0 + p(10) + p(20) + p(01) + p(11) + p(21)⋅0 го имав p(11) пропуштено!!!
p(Y = 0) = p(X₁ = 0, X₂ = 0)⋅p(Y = 0|X₁ = 0, X₂ = 0) + p(X₁ = 0, X₂ = 1)⋅p(Y = 0|X₁ = 0, X₂ = 1) + p(X₁ = 1, X₂ = 1)⋅p(Y = 0|X₁ = 1, X₂ = 1) = \mathchoicep(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);
p(Y = 1) = \mathchoice(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2); p(Y = 2) = \mathchoice(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)
H(Y) = − ⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠
p(00) + p(10) + p(20) + p(01) + p(11) + p(21) = 1 p(00) = 1 − p(10) + p(20) + p(01) + p(11) + p(21)

\strikeout off\uuline off\uwave off\mathchoicep(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;

\strikeout off\uuline off\uwave offa + b + c + d + e + f = 1

\strikeout off\uuline off\uwave offH(Y) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = p(10) + p(20) + p(01) + p(11) = b + c + d + e

I(X₁, X₂;Y) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − e
a = (4)/(9) − (d)/(2) − (e)/(2); b = (2)/(9) − c − d − e
p(x₂) = 0; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 1 0 0 0 0.5 0.5 0 0.5 0.5 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦
H(Y|X₁|X₂ = 0) = ∑_x₁,p(x₁)⋅H(Y|X₁ = x₁) = p(x₀)⋅0 + p(x₁)⋅1 + p(x₂)⋅1
p(x₂) = 1; ⎡⎢⎢⎢⎣ p(y₀) p(y₁) p(y₂₎ ⎤⎥⎥⎥⎦ = ⎡⎢⎢⎢⎣ 0.5 0.5 0 0.5 0.5 0 0 0 1 ⎤⎥⎥⎥⎦⎡⎢⎢⎢⎣ p(x₀) p(x₁) p(x₂₎ ⎤⎥⎥⎥⎦
H(Y|X₁|X₂ = 0) = ∑_x₁,p(x₁)⋅H(Y|X₁ = x₁) = p(x₀)⋅1 + p(x₁)⋅1
H(Y|X₁X₂) = ∑_x₂,p(x₂)⋅H(Y|X₁X₂ = x₂) = p(x₂ = 0)⋅(p(x₁) + p(x₂)) + p(x₂ = 1)⋅(p(x₀) + p(x₁)) = p₂(0)⋅p₁(1) + p₂(0)⋅p₁(2) + p₂(1)⋅p₁(0) + p₂(1)⋅p₁(1)

\strikeout off\uuline off\uwave offI(X₁, X₂;Y) = H(Y) − H(Y|X₁, X₂) = H(X₁, X₂) − H(X₁, X₂|Y)

Сега сакам да го пресметам H(Y) како што треба:
p(Y = 0|X₂ = 0) = p(X₁ = 0) = p₁(0); p(Y = 1|X₂ = 0) = (p(X₁ = 1))/(2) + (p(X₁ = 2))/(2) = (p₁(1))/(2) + (p₁(2))/(2); p(Y = 2|X₂ = 0) = (p₁(1))/(2) + (p₁(2))/(2)
p(Y = 0|X₂ = 1) = (p(X₁ = 0))/(2) + (p(X₁ = 1))/(2) = (p₁(0))/(2) + (p₁(1))/(2); p(Y = 1|X₂ = 1) = (p(X₁ = 0))/(2) + (p(X₁ = 1))/(2) = (p₁(0))/(2) + (p₁(1))/(2); p(Y = 2|X₂ = 1) = p(X₁ = 2) = p₁(2);
\mathchoicep(Y = 0) = p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠; p(Y = 1) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2); p(Y = 2) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂p(Y = 0) = p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠; p(Y = 1) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2); p(Y = 2) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂p(Y = 0) = p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠; p(Y = 1) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2); p(Y = 2) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂p(Y = 0) = p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠; p(Y = 1) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2); p(Y = 2) = p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂

\strikeout off\uuline off\uwave offI(X₁, X₂;Y) = H⎛⎝p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠, p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2), p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂⎞⎠ − p₂₀⋅p₁₁ − p₂₀⋅p₁₂ − p₂₁⋅p₁₀ − p₂₁⋅p₁₁

\strikeout off\uuline off\uwave off\mathchoicep₂₀ = a; p₂₁ = b; p₁₀ = c; p₁₁ = d; p₁₂ = e;p₂₀ = a; p₂₁ = b; p₁₀ = c; p₁₁ = d; p₁₂ = e;p₂₀ = a; p₂₁ = b; p₁₀ = c; p₁₁ = d; p₁₂ = e;p₂₀ = a; p₂₁ = b; p₁₀ = c; p₁₁ = d; p₁₂ = e;

\strikeout off\uuline off\uwave off(ac + b(1 ⁄ 2 c + 1 ⁄ 2 d))ln(ac + b(1 ⁄ 2 c + 1 ⁄ 2 d)) − (a(1 ⁄ 2 d + 1 ⁄ 2 e) + b(1 ⁄ 2 c + 1 ⁄ 2 d))ln(a(1 ⁄ 2 d + 1 ⁄ 2 e) + b(1 ⁄ 2 c + 1 ⁄ 2 d)) − a(1 ⁄ 2 d + 1 ⁄ 2 e) − be⋅log₂(a(1 ⁄ 2 d + 1 ⁄ 2 e) − be)

\strikeout off\uuline off\uwave offI(X₁, X₂;Y) = H⎛⎝p₂₀p₁₀ + p₂₁⎛⎝(p₁₀ + p₁₁)/(2)⎞⎠, p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅(p₁₀ + p₁₁)/(2), p₂₀⋅(p₁₁ + p₁₂)/(2) + p₂₁⋅p₁₂⎞⎠ − p₂₀⋅p₁₁ − p₂₀⋅p₁₂ − p₂₁⋅p₁₀ − p₂₁⋅p₁₁

Мислам дека униформна распределба е оптимална за p(X₁).
I(X₁, X₂;Y) = H⎛⎝(p₂₀)/(3) + p₂₁⎛⎝(1)/(3)⎞⎠, p₂₀⋅(1)/(3) + p₂₁⋅(1)/(3), p₂₀⋅(1)/(3) + (p₂₁)/(3)⎞⎠ − p₂₀⋅(1)/(3) − p₂₀⋅(1)/(3) − p₂₁⋅(1)/(3) − p₂₁⋅(1)/(3)
I(X₁, X₂;Y) = H⎛⎝(p₂₀)/(3) + (p₂₁)/(3), (p₂₀)/(3) + (p₂₁)/(3), (p₂₀)/(3) + (p₂₁)/(3)⎞⎠ − (p₂₀)/(3) − (p₂₀)/(3) − (p₂₁)/(3) − (p₂₁)/(3)
I(X₁, X₂;Y) = − log₂⎛⎝(p₂₀)/(3) + (p₂₁)/(3)⎞⎠ − (2⋅p₂₀)/(3) − (2⋅p₂₁)/(3)
Во Maple ги добив следниве вредности
d = 1 − c − e
{{a = 0, c = 1 ⁄ 3, e = 1 ⁄ 2}, {a = 1, c = 1 ⁄ 2, e = 1 ⁄ 3}}
e = 1 − d − e
{{a = 0, d = 1 ⁄ 6, e = 1 ⁄ 2}, {a = 1, d = 1 ⁄ 6, e = 1 ⁄ 3}}
За првото решение:

c = 1 − d − e = 1 − (1)/(6) − (1)/(2) = 1 − (1 + 3)/(6) = 1 − (2)/(3) = (1)/(3) во согласност е со резултатот за d = 1 − c − e.

(a, b, c, d, e) = ⎛⎝0, 1, (1)/(3), (1)/(6), (1)/(2)⎞⎠
За второто решение:

c = 1 − d − e = 1 − (1)/(6) − (1)/(3) = 1 − (1 + 2)/(6) = 1 − (1)/(2) = (1)/(2) во согласност е со резултатот за d = 1 − c − e.

(a, b, c, d, e) = ⎛⎝1, 0, (1)/(2), (1)/(6), (1)/(3)⎞⎠
За овие вредности
I(X₁, X₂;Y) = 1

Моево изведување ми изгледа добро но се прашувам каде е шумот???

Врз основ на 5↑ да го најдам \strikeout off\uuline off\uwave offI(X₁;Y₁|X₂) за да потоa побарам минимум.

I(X₁;Y₁|X₂) = H(Y₁) − H(Y₁|X₁, X₂) = H(Y₁) − ⎲⎳_x₁, x₂p(x₁, x₂)⋅H(Y₁|X₁X₂ = x₁, x₂) = H(Y₁) − p(0, 0)H(Y₁|00) + p(01)H(Y₁|01) + p(0, 2)H(Y₁|02) + p(1, 0)H(Y₁|10) + p(11)H(Y₁|11) + p(1, 2)H(Y₁|12) = H(Y₁) − 0 = H(Y₁)

C = sup_p(x1, x2)min{I(X₁, X₂;Y), I(X₁;Y₁|X₂)}

I(X₁;Y₁|X₂) = H(Y₁)

\strikeout off\uuline off\uwave offI(X₁, X₂;Y) = H(Y) − (p(X₂ = 0)⋅p(X₁ = 1) + p(X₂ = 0)⋅p(X₁ = 2) + p(X₂ = 1)⋅p(X₁ = 0) + p(X₂ = 1)⋅p(X₁ = 1))

I(X₁, X₂;Y) ≤ I(X₁;Y₁|X₂)
C = sup_{p(x₁, x₂)}(I(X₁, X₂;Y))
H(X, f(X)) = H(X) + H(f(X)|X) = H(f(X)) + H(X|f(X)); H(f(X)|X) = 0; H(X) > H(f(x));
Бараме капацитет за деградиран релеен канал, а не го користам изразот кој го дефинира

\strikeout off\uuline off\uwave offp(y, y₁|x₁, x₂) = p(y|x₁, x₂)⋅p(y₁|x₁, x₂)

\strikeout off\uuline off\uwave offp(y, y₁|x₁, x₂) = p(y|x₁, x₂)⋅p(y₁|x₁, x₂) Ова врска нема

for degraded: \mathchoiceX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → YX₁ → (X₂, Y₁) → Y for reversly degraded:\mathchoiceX₁ → (X₂, Y) → Y₁X₁ → (X₂, Y) → Y₁X₁ → (X₂, Y) → Y₁X₁ → (X₂, Y) → Y₁

\strikeout off\uuline off\uwave offI(X₁X₂;Y) + I(X₁X₂;Y₁|Y) = H(Y₁) + I(X₁;Y₁|X₂) + I(X₂;Y|Y₁)

I(X₁X₂;Y) + I(X₁;Y₁|Y) + I(X₂;Y₁|Y, X₁)

Овој обид е од второто читање на чланакот (после EIT chapter 15).
Ми изгледа многу едноставен и точен. Најмногу му верувам. Сепак не се добиваат вредностите што ги добил Sato.

H(Y|X₁X₂) = ⎲⎳_x₁x₂yp(x₁x₂)H(y|x₁x₂) = 2⋅p⋅0 + 4⋅p⋅log2 = 4⋅p⋅log2 = 4⋅p⋅log2

I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = − 6⋅plog(2p) − H(Y|X₁X₂) = − 6⋅p⋅log(2p) − 4p⋅log2
(d)/(dp)(I(X₁X₂;Y)) = 0 → p = 0.116; → max_pI(X₁X₂;Y) = 0.8 ternary symbols = 1.263 bits
0.116⋅6 = 0.696
Не бива со извод зошто после не излегува вкупната веројатност 1. Затоа мора со униформна распределба на p(x₁x₂) = p = (1)/(6).
N⎡⎣1 − 4⋅(1)/(6)⋅Log[3, 2]⎤⎦ = 0.57938 ternary digits/transmission
N⎡⎣Log[2, 3] − 4⋅(1)/(6)⋅Log[2, 2]⎤⎦ = 0.918296 bits/transmission
y = log₃(x) → x = 3^y|⋅log₂() → log₂x = y⋅log₂(3) → y = (log₂(x))/(log₂(3))
y = log₂(x) → x = 2^y|⋅log₃() → log₃x = y⋅log₃(2) → y = (log₃(x))/(log₃(2))
Види ги примерите во Network Information Theory од A. E. Gamal. Таму ќе ти стане јасно зошто не ти излегуваат вреднотите како горе.
Ова е добро ама капацитетот е
C ≥ max_p(x, y)min{I(X₁, X₂;Y₂)I(X₁;Y₂|X₂)}
- Значи не го имам пресметано I(X₁;Y₂|X₂)
Ама што е во случајов Y₂?????
I(X₁;Y₂|X₂) = H(Y|X₂) − H(Y|X₁X₂)
H(Y|X₂) = ?
H(Y|X₂) = p(X₂ = 0)H(Y|X₂ = 0) + p(X₂ = 1)H(Y|X₂ = 1)
y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 y|x₁x₂ y₀ y₁ y₂ 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1
H(Y|X₂ = 0)
H(Y|X₁X₂ = 0) = p(X₁ = 0, X₂ = 0)⋅H(Y|X₁ = 0, X₂ = 0) + p(X₁ = 1, X₂ = 0)⋅H(Y|X₁ = 1, X₂ = 0) + p(X₁ = 2, X₂ = 0)⋅H(Y|X₁ = 2, X₂ = 0) =
= p(X₁ = 1, X₂ = 0)log2 + p(X₁ = 2, X₂ = 0)log2
H(Y|X₁X₂ = 1) = p(X₁ = 0, X₂ = 1)⋅H(Y|X₁ = 0, X₂ = 1) + p(X₁ = 1, X₂ = 1)⋅H(Y|X₁ = 1, X₂ = 1) + p(X₁ = 2, X₂ = 1)⋅H(Y|X₁ = 2, X₂ = 1) =
= p(X₁ = 0, X₂ = 1)log2 + p(X₁ = 1, X₂ = 1)log2
H(Y|X₂) = p(X₂ = 0)H(Y|X₂ = 0) + p(X₂ = 1)H(Y|X₂ = 1) =
= p(X₂ = 0)(p(X₁ = 1|X₂ = 0) + p(X₁ = 2|X₂ = 0))log2 + p(X₂ = 1)(p(X₁ = 0|X₂ = 1) + p(X₁ = 1|X₂ = 1))log2
= (p(X₁ = 1, X₂ = 0) + p(X₁ = 2, X₂ = 0) + p(X₁ = 0, X₂ = 1) + p(X₁ = 1, X₂ = 1))log2 = 4plog2
I(X₁;Y|X₂) = H(Y|X₂) − H(Y|X₁X₂) = 4plog2 − 2p⋅log2 = 2plog2 ternary digits/transmission
I(X₁;Y|X₂) = 2p bits/transmission
maxI(X₁;Y|X₂) = ||p = (1)/(6)|| = (1)/(3)

Овој обид е после El Gamal, Network Information Theory Ch.16.

p(y|x₁x₂) p(x₁x₂, y)
y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 p₁ 0 0 p₁ 10 0 0.5p₂ 0.5p₂ p₂ 20 0 0.5p₃ 0.5p₃ p₃ 01 0.5p₄ 0.5p₄ 0 p₄ 11 0.5p₅ 0.5p₅ 0 p₅ 21 0 0 p₆ p₆ p(y) 1 ⁄ 3 1 ⁄ 3 1 ⁄ 3

(16) p₁ + (p₄ + p₅)/(2) = (1)/(3) (p₂ + p₃)/(2) + (p₄ + p₅)/(2) = (1)/(3) (p₂ + p₃)/(2) + p₆ = (1)/(3)

H(Y|X₁X₂) = ⎲⎳_x₁x₂yp(x₁x₂)H(y|x₁x₂) = 2⋅p⋅0 + 4⋅p⋅log2 = 4⋅p⋅log2 = 4⋅p⋅log2

I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = − 6⋅plog(2p) − H(Y|X₁X₂) = − 6⋅p⋅log(2p) − 4p⋅log2
(d)/(dp)(I(X₁X₂;Y)) = 0 → p = 0.116; → max_pI(X₁X₂;Y) = 0.8 ternary symbols = 1.263 bits
0.116⋅6 = 0.696
Не бива со извод зошто после не излегува вкупната веројатност 1. Затоа мора со униформна распределба на p(x₁x₂) = p = (1)/(6).
N⎡⎣1 − 4⋅(1)/(6)⋅Log[3, 2]⎤⎦ = 0.57938 ternary digits/transmission
N⎡⎣Log[2, 3] − 4⋅(1)/(6)⋅Log[2, 2]⎤⎦ = 0.918296 bits/transmission
Следново изведување е ептен точно. Дефинитивно не можам да најдам грешка. Евентуално да дозволиш p(y) да не биде униформно

Ги решив во Мапле 16↑

y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 1 ⁄ 6 0 0 1 ⁄ 6 10 0 0.5(1 ⁄ 3 − x) 0.5(1 ⁄ 3 − x) 1 ⁄ 3 − x 20 0 0.5x 0.5x x 01 0.5(1 ⁄ 3 − x) 0.5(1 ⁄ 3 − x) 0 1 ⁄ 3 − x 11 0.5x 0.5x 0 x 21 0 0 1 ⁄ 6 1 ⁄ 6 p(y) 1 ⁄ 3 1 ⁄ 3 1 ⁄ 3
p₂ + p₃ = (1)/(3) → p₂ = 1 ⁄ 3 − p₃ = 1 ⁄ 3 − x
p₄ + p₅ = (1)/(3) → p₄ = 1 ⁄ 3 − p₅ = 1 ⁄ 3 − y
I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = log3 − H(Y|X₁X₂)
H(Y|X₁X₂ = 00) = H(Y|X₁X₂ = 21) = (1⋅log1) = 0
H(Y|X₁X₂ = 10) = p(Y = 1|(X₁X₂) = 10)log(p(Y = 1|(X₁X₂) = 10)) + p(Y = 1|(X₁X₂) = 10)log(p(Y = 1|(X₁X₂) = 10))
= (1)/(2)log2 + (1)/(2)log2 = log2
H(Y|X₁X₂ = 20) = H(Y|X₁X₂ = 01) = H(Y|X₁X₂ = 11) = log2

H(Y|X₁X₂) = ⎲⎳_x₁x₂yp(x₁x₂)H(y|x₁x₂) = 2⋅(1)/(6)⋅0 + (2⋅x + 2 ⁄ 3 − 2x)⋅log2 = 2 ⁄ 3⋅log2

I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = 1 − (2 ⁄ 3)⋅log2
max[I(X₁X₂;Y)] = 1 − (2)/(3)log2 ternary digits/transmission
N⎡⎣1 − (2)/(3)⋅Log[3, 2]⎤⎦ = 0.57938
N⎡⎣Log[2, 3] − (2)/(3)⋅Log[2, 2]⎤⎦ = 0.918296 bits/transmission
Исто како при претпоставката дека p(x₁x₂) е униформно распределена
I(X₁;Y₂|X₂) = I(X₁;Y₂) = H(X₁) − H(Y₂|X₁) = log3 = 1 ternary digits/transmission
N[Log[2, 3]] = 1.58496
Min[0.92, 1.585] = 0.92
Не мора да се глупираш и да пишуваш log2. Најлесно е цело време да работиш со log₂ и одма ќе добиеш резултат во бити.

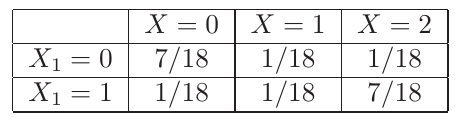
Од NIT Lecture Notes Relay with limmited lookahead. figure Optimization PDF.png

y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 7 ⁄ 18 0 0 7 ⁄ 18 10 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 20 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 01 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 11 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 21 0 0 7 ⁄ 18 7 ⁄ 18 p(y) 4 ⁄ 9 1 ⁄ 9 4 ⁄ 9
(8)/(36) + (7)/(9) = 1 (7)/(18) + (2)/(36) = (4)/(9)
N[7 ⁄ 18] = 0.388889
I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂)
H(Y) = N⎡⎣(8)/(9)Log[2, 9 ⁄ 4] + (1)/(9)Log[2, 9]⎤⎦ = 1.39215
H(Y|X₁X₂ = 00) = H(Y|X₁X₂ = 21) = (1⋅log1) = 0
H(Y|X₁X₂ = 10) = p(Y = 1|(X₁X₂) = 10)log(p(Y = 1|(X₁X₂) = 10)) + p(Y = 1|(X₁X₂) = 10)log(p(Y = 1|(X₁X₂) = 10))
= (1)/(2)log₂2 + (1)/(2)log₂2 = 1
H(Y|X₁X₂ = 20) = H(Y|X₁X₂ = 01) = H(Y|X₁X₂ = 11) = log₂2 = 1

H(Y|X₁X₂) = ⎲⎳_x₁x₂yp(x₁x₂)H(y|x₁x₂) = 2⋅(7)/(8)⋅0 + (4)/(18)⋅1 = 2 ⁄ 9

N[2 ⁄ 9] = 0.222222
I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = 1.39215 − 0.222222 = 1.16993
N[Log[2, 9 ⁄ 4]] = 1.16993
(8)/(9)log₂⎛⎝(9)/(4)⎞⎠ + (1)/(9)log₂(9) − (2)/(9) = (8)/(9)log₂(9) + (1)/(9)log₂(9) − (8)/(9)log₂(4) − (2)/(9) = (8)/(9)log₂(9) + (1)/(9)log₂(9) − (16)/(9) − (2)/(9) = log(9) − (18)/(9) = log(9) − 2 = log(9) − log₂(4) = \mathchoicelog₂(9 ⁄ 4)log₂(9 ⁄ 4)log₂(9 ⁄ 4)log₂(9 ⁄ 4)

\strikeout off\uuline off\uwave off x₂ = 0 x₂ = 1 \overset x₁ = 0 x₂ = 1 x₃ = 2 ⎡⎢⎣ 0.35431 0.072845 0.072845 0.072845 0.072845 0.35431 ⎤⎥⎦

y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 0.35431 0 0 0.35431 10 0 0.0364225 0.0364225 0.072845 20 0 0.0364225 0.0364225 0.072845 01 0.0364225 0.0364225 0 0.072845 11 0.0364225 0.0364225 0 0.072845 21 0 0 0.35431 0.35431 p(y) 0.427155 0.14569 0.427155

H(Y|X₁X₂) = ⎲⎳_x₁x₂yp(x₁x₂)H(y|x₁x₂) = 2⋅0.35431⋅0 + 4⋅0.072845⋅1

4⋅0.072845⋅1 = 0.29138
I(X₁X₂;Y) = H(Y) − H(Y|X₁X₂) = 1.45326 − 0.29138 = 1.16188
Фала богу!!! Немам поим каде сум грешел до сега!

Барање на отпимална дистрибуција
——————————————————————————–——————————
y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 a 0 0 a 10 0 0.5b 0.5b b 20 0 0.5c 0.5c c 01 0.5d 0.5d 0 d 11 0.5e 0.5e 0 e 21 0 0 f f p(y) a + 0.5(d + e) 0.5(b + c + d + e) f + 0.5(b + c)

\strikeout off\uuline off\uwave offH(Y|X₁, X₂) = ∑_x₁, x₂p(x₁, x₂)⋅H(Y|X₂ = x₂, X₁ = x₁) = p(0, 0)H(Y|00) + p(10)H(Y|10) + p(20)H(Y|20) + p(01)H(Y|01) + p(11)H(Y|11) + p(2, 1)H(Y|21)

= p(00)⋅0 + \mathchoicep(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11)p(10) + p(20) + p(01) + p(11) + p(21)⋅0 го имав p(11) пропуштено!!!
p(Y = 0) = \mathchoicep(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2);p(00) + (p(01) + p(11))/(2); = a + (d + e)/(2)
p(Y = 1) = \mathchoice(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2)(p(10) + p(20))/(2) + (p(01) + p(11))/(2) = (b + c)/(2) + (d + e)/(2); p(Y = 2) = \mathchoice(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21)(p(10) + p(20))/(2) + p(21) = (b + c)/(2) + f
H(Y) = − ⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝p(00) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + (p(01) + p(11))/(2)⎞⎠ − ⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠⋅log₂⎛⎝(p(10) + p(20))/(2) + p(21)⎞⎠
p(00) + p(10) + p(20) + p(01) + p(11) + p(21) = 1 p(00) = 1 − p(10) + p(20) + p(01) + p(11) + p(21)

\strikeout off\uuline off\uwave off\mathchoicep(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;p(00) = a; p(10) = b; p(20) = c; p(01) = d; p(11) = e; p(21) = f;

\strikeout off\uuline off\uwave offa + b + c + d + e + f = 1

\strikeout off\uuline off\uwave offH(Y) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠

\mathchoiceI(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − eI(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − eI(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − eI(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − ⎛⎝a + (d + e)/(2)⎞⎠⋅log₂⎛⎝a + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠⋅log₂⎛⎝(b + c)/(2) + (d + e)/(2)⎞⎠ − ⎛⎝(b + c)/(2) + f⎞⎠⋅log₂⎛⎝(b + c)/(2) + f⎞⎠ − b − c − d − e

Да симплифицирам:

y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 a 0 0 a 10 0 0.5b 0.5b b 20 0 0.5b 0.5b b 01 0.5b 0.5b 0 b 11 0.5b 0.5b 0 b 21 0 0 a a p(y) a + b 2b a + b
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − 2(a + b)⋅log₂(a + b) − (2b)⋅log₂(2b) − 4b
2a + 4b = 1 → a = (1 − 4⋅b)/(2)
− 2⎛⎝(1 − 4⋅b)/(2) + b⎞⎠⋅log₂⎛⎝(1 − 4⋅b)/(2) + b⎞⎠ − (2b)⋅log₂(2b) − 4b = − 2⎛⎝(1 − 4⋅b + 2b)/(2)⎞⎠⋅log₂⎛⎝(1 − 4⋅b + 2b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b = − 2⎛⎝(1 − 2⋅b)/(2)⎞⎠⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
I(X₁, X₂;Y) = − (1 − 2⋅b)⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
Од Maple добив:
(d)/(dp)(I(X₁X₂;Y)) = 0 → b = (1)/(8) ; a = (1 − 4⋅1 ⁄ 18)/(2) = (7)/(18)
max_pI(X₁X₂;Y) = \mathchoice1.16991.16991.16991.1699 bits
y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 7 ⁄ 18 0 0 7 ⁄ 18 10 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 20 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 01 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 11 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 21 0 0 7 ⁄ 18 7 ⁄ 18 p(y) 4 ⁄ 9 1 ⁄ 9 4 ⁄ 9
Да ова е решението што го дава Cover за R_UG = max_p(x₁x₂)I(X₁X₂;Y) докажано!!!

Пресметка на вториот член од cutset theorem.

p(y|x₁x₂) p(x₁x₂y)
y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) p(x₂) 00 7 ⁄ 18 0 0 7 ⁄ 18 x 10 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 y 20 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 y 01 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 y 11 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 y 21 0 0 7 ⁄ 18 7 ⁄ 18 x p(y) 4 ⁄ 9 1 ⁄ 9 4 ⁄ 9
(p(x₁x₂))/(p(x₂)) = p(x₁|x₂)
2x + 4y = 1 → x = (1 − 4y)/(2) → y = (1 − 2x)/(4)
I(X₁;Y₁|X₂) = H(Y₁|X₂) − \cancelto0H(Y₁|X₁X₂) = H(X₁|X₂) − \cancelto0H(X₁|Y₁X₂) = H(Y₁|X₂) = H(X₁|X₂)?
H(X₁|X₂) = − ∑_x₁x₂p(x₁x₂)logp(x₁|x₂) = − (4)/(18)log(1)/(18y) − (14)/(18)log⎛⎝(7)/(18x)⎞⎠ = (4)/(18)log18y + (14)/(18)log⎛⎝(18x)/(7)⎞⎠ = (4)/(18)log18⋅(1 − 2x)/(4) + (14)/(18)log⎛⎝(18x)/(7)⎞⎠
(d)/(dp)(I(X₂;Y₁|X₂)) = 0 → x = 0.3181181 ;
(1 − 2⋅0.3181182)/(4) = 0.0909409
2⋅0.318181 + 4⋅0.0909409 = 1.00013
I(X₂;Y₁|X₂) = 0.0453
——————————————————————————–——————————————————–
y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) p(x₂) 00 7 ⁄ 18 0 0 7 ⁄ 18 x 10 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 x 20 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 x 01 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 y 11 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 y 21 0 0 7 ⁄ 18 7 ⁄ 18 y p(y) 4 ⁄ 9 1 ⁄ 9 4 ⁄ 9
x + y = 1 → y = 1 − x
H(X₁|X₂) = − ∑_x₁x₂p(x₁x₂)logp(x₁|x₂) = − (2)/(18)log(1)/(18x) − (7)/(18)log⎛⎝(7)/(18x)⎞⎠ − (2)/(18)log(1)/(18y) − (7)/(18)log⎛⎝(7)/(18y)⎞⎠ = (2)/(18)log18x + (7)/(18)log⎛⎝(18x)/(7)⎞⎠ + (2)/(18)log18y + (7)/(18)log⎛⎝(18y)/(7)⎞⎠
= (2)/(18)log(18²xy) + (7)/(18)log⎛⎝(18²xy)/(7²)⎞⎠ = (2)/(18)log(18²x⋅(1 − x)) + (7)/(18)log⎛⎝(18²)/(7²)x⋅(1 − x)⎞⎠ = (2)/(18)log(324⋅(x − x²)) + (7)/(18)log⎛⎝(324)/(49)⋅(x − x²)⎞⎠
(18²)/(7²) = (324)/(49)
Со користење на Maple и изводи:
H(X₁|X₂) = 0.986
Нема потреба од изводи зошто се е дефинирано:
p(x₁x₂) p(x₁|x₂)
x₁|x₂ 0 1 p(x₁) 0 7 ⁄ 18 1 ⁄ 18 8 ⁄ 18 1 1 ⁄ 18 1 ⁄ 18 2 ⁄ 18 2 1 ⁄ 18 7 ⁄ 18 8 ⁄ 18 p(x₂) 1 ⁄ 2 1 ⁄ 2 x₁|x₂ 0 1 0 14 ⁄ 18 2 ⁄ 18 1 2 ⁄ 18 2 ⁄ 18 2 2 ⁄ 18 14 ⁄ 18
H(X₁|X₂) = (14)/(18)log₂⎛⎝(18)/(14)⎞⎠ + (4)/(18)log₂⎛⎝(18)/(2)⎞⎠
N⎡⎣(14)/(18)⋅Log⎡⎣2, (18)/(14)⎤⎦ + (4)/(18)⋅Log⎡⎣2, (18)/(2)⎤⎦⎤⎦ = 0.986427

Веројатно треба со башка вредности за p(x₁x₂):

p(x₁x₂) p(x₁|x₂)
x₁|x₂ 0 1 p(x₁) 0 a b a + b 1 b b 2b 2 b a a + b p(x₂) a + 2b a + 2b p(x₂) 1 ⁄ 2 1 ⁄ 2 x₁|x₂ 0 1 0 2a 2b 1 2b 2b 2 2b 2a
2a + 4b = 1 → b = (1 − 2a)/(4) → a + 2b = (1)/(2)
H(X₁|X₂) = − ∑_x₁x₂p(x₁x₂)logp(x₁|x₂) = 2⋅a⋅log(1)/(2a) + 4⋅b⋅log(1)/(2b) = 2⋅a⋅log(1)/(2a) + 4⋅(1 − 2a)/(4)⋅log(4)/(2 − 4a)
Maple
a = 1 ⁄ 6
b = (1 − 2⋅1 ⁄ 6)/(4) = (1)/(6)
I(X₁;Y₁|X₂) = H(X₁|X₂) = 1.585

Уште еднаш пресметка на вториот член од Cutset Theorem
y|x₁x₂ y₀ y₁ y₂ 00 1 0 0 10 0 0.5 0.5 20 0 0.5 0.5 01 0.5 0.5 0 11 0.5 0.5 0 21 0 0 1 y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 a 0 0 a 10 0 0.5b 0.5b b 20 0 0.5b 0.5b b 01 0.5b 0.5b 0 b 11 0.5b 0.5b 0 b 21 0 0 a a p(y) a + b 2b a + b
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = − 2(a + b)⋅log₂(a + b) − (2b)⋅log₂(2b) − 4b
2a + 4b = 1 → a = (1 − 4⋅b)/(2)
− 2⎛⎝(1 − 4⋅b)/(2) + b⎞⎠⋅log₂⎛⎝(1 − 4⋅b)/(2) + b⎞⎠ − (2b)⋅log₂(2b) − 4b = − 2⎛⎝(1 − 4⋅b + 2b)/(2)⎞⎠⋅log₂⎛⎝(1 − 4⋅b + 2b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b = − 2⎛⎝(1 − 2⋅b)/(2)⎞⎠⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
I(X₁, X₂;Y) = − (1 − 2⋅b)⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
Од Maple добив:
(d)/(db)(I(X₁X₂;Y)) = 0 → b = (1)/(1g(8) ; a = (1 − 4⋅1 ⁄ 18)/(2) = (7)/(18)
max_pI(X₁X₂;Y) = \mathchoice1.16991.16991.16991.1699 bits
y|x₁x₂ y₀ y₁ y₂ p(x₁x₂) 00 7 ⁄ 18 0 0 7 ⁄ 18 10 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 20 0 1 ⁄ 36 1 ⁄ 36 1 ⁄ 18 01 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 11 1 ⁄ 36 1 ⁄ 36 0 1 ⁄ 18 21 0 0 7 ⁄ 18 7 ⁄ 18 p(y) 4 ⁄ 9 1 ⁄ 9 4 ⁄ 9
Да ова е решението што го дава Cover за R_UG = max_p(x₁x₂)I(X₁X₂;Y) докажано!!!
За време на читање на докторатот
I(X₁;Y₁|X₂) = H(Y₁|X₂) − H(Y₁|X₁X₂) = H(Y₁) = H(X₁) = − p₁log(p₁) − p₂log(p₂) − p₃log(p₃) = − 2⋅(a + b)log(a + b) − 2b⋅log(2b)
p(x₁x₂)
x₁ ⁄ x₂ 0 1 p(x₁) 0 a b a + b 1 b b 2b 2 b a a + b p(x₂) a + 2b a + 2b
− 2⋅(a + b)log(a + b) − 2b⋅log(2b) = − (1 − 2⋅b)⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
a = (1 − 4⋅b)/(2)
− 2⋅((1 − 4⋅b)/(2) + b)log⎛⎝(1 − 4⋅b)/(2) + b⎞⎠ − 2b⋅log(2b) = − (1 − 2⋅b)⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b
(1 − 4⋅b)/(2) + b = (1 − 4⋅b + 2b)/(2) = (1 − 2⋅b)/(2)
− 2⋅((1 − 2⋅b)/(2))log⎛⎝(1 − 2⋅b)/(2)⎞⎠ − 2b⋅log(2b) = − (1 − 2⋅b)⋅log₂⎛⎝(1 − 2⋅b)/(2)⎞⎠ − (2b)⋅log₂(2b) − 4b → b = 0
Значи двете функции се сечат за b = 0.
(d)/(db)I(X₁;Y₁|X₂) = 0 → b = (1)/(6) → a = (1)/(6) → I(X₁;Y₁|X₂) = 1.585
Дефинитивно I(X₁X₂;Y) ≥ I(X₁;Y₁|X₂)
Пак истото се добива.
Последно што пробав во Maple да барам извод по a после по b и да ги решам равенките после. Не се добиваат добри резултати.

The achievability of \mathchoiceC₀ = sup_p(x₁)max_x₂I(X₁;Y|x₂)C₀ = sup_p(x₁)max_x₂I(X₁;Y|x₂)C₀ = sup_p(x₁)max_x₂I(X₁;Y|x₂)C₀ = sup_p(x₁)max_x₂I(X₁;Y|x₂) in Theorem 2 follows immediately form Shannon’s basic result [5] if we set X_2i = x₂, i = 1, 2, ... . Also the achievability of C_FB in Theorem 3 is a simple corollary of Theorem 1, when it is realized that the feedback relay channel is a degraded relay channel. The converses will be delayed until Section III.

We are left only with the proof of Theorem 1 - the achievability of C for the degraded relay channel. We begin with a brief outline of the proof. We consider B blocks , each of n symbols. A sequence of B − 1 messages w_i ∈ [1, 2^nR], i = 1, 2, ..., B − 1 will be sent over the channel in nB transmissions. (Note that as B → ∞, for fixed n, the rate \mathchoiceR(B − 1) ⁄ BR(B − 1) ⁄ BR(B − 1) ⁄ BR(B − 1) ⁄ B is arbitrary close to R.) Многу е важно да се сконта дека праќа B − 1 пораки во B блокови. Ако претпоставиш дека еден блок се прaќа во една употреба на каналот (на пример n паралелни бинарни канали=еден блок) тогаш доколку нема грешки во преносот во приемникот ќе препознаеш B-1 блокови за B употреби на каналот т.е капацитетот ќе биде (B − 1) ⁄ B. Секогаш потсеќај се на noisy typewriter. Што и да правиш тој пола од буквите ги греши (шум) па на излез препознаваш само 13 од вкупно 26. Затоа капацитетот во бити беше log₂(13) или во букви 0.5. (после EIT) Мислам дека едната порака не е стигната во приемникот затоа што сеуште се процесира во релето.

In each n-block b = 1, 2, ..., B we shall use the same doubly indexed set of codewords

(17) \mathchoiceC\mathnormal = {x₁(w_b|s_b), x₂(s_b)}; w_b ∈ [1, 2^nR], s_b ∈ [1, 2^nR₀], x₁(⋅|⋅) ∈ X^\mathnormaln_\mathnormal1, x₂(⋅) ∈ X^\mathnormaln_\mathnormal2.C\mathnormal = {x₁(w_b|s_b), x₂(s_b)}; w_b ∈ [1, 2^nR], s_b ∈ [1, 2^nR₀], x₁(⋅|⋅) ∈ X^\mathnormaln_\mathnormal1, x₂(⋅) ∈ X^\mathnormaln_\mathnormal2.C\mathnormal = {x₁(w_b|s_b), x₂(s_b)}; w_b ∈ [1, 2^nR], s_b ∈ [1, 2^nR₀], x₁(⋅|⋅) ∈ X^\mathnormaln_\mathnormal1, x₂(⋅) ∈ X^\mathnormaln_\mathnormal2.C\mathnormal = {x₁(w_b|s_b), x₂(s_b)}; w_b ∈ [1, 2^nR], s_b ∈ [1, 2^nR₀], x₁(⋅|⋅) ∈ X^\mathnormaln_\mathnormal1, x₂(⋅) ∈ X^\mathnormaln_\mathnormal2.

We shall also need a partition

(18) \mathchoiceS = \mathnormal{S₁, S₂, ..., S_2^nR₀} of W = \mathnormal{1, 2, ...2^nR} into 2^nR₀ cells, S_i∩S_j = 0, i ≠ j, ∪S_i = WS = \mathnormal{S₁, S₂, ..., S_2^nR₀} of W = \mathnormal{1, 2, ...2^nR} into 2^nR₀ cells, S_i∩S_j = 0, i ≠ j, ∪S_i = WS = \mathnormal{S₁, S₂, ..., S_2^nR₀} of W = \mathnormal{1, 2, ...2^nR} into 2^nR₀ cells, S_i∩S_j = 0, i ≠ j, ∪S_i = WS = \mathnormal{S₁, S₂, ..., S_2^nR₀} of W = \mathnormal{1, 2, ...2^nR} into 2^nR₀ cells, S_i∩S_j = 0, i ≠ j, ∪S_i = W

The partition S will allow us to send information to the receiver using the random binning proof of the source coding theorem of Seplian and Wolf [7].

The choice of C and S achieving C will be random, but the description of the random code and partition will be delayed until the use of the code is described. For the time being, the code should be assumed fixed.

We pick up the story in block i − 1. First, let us assume that the receiver y knows w_i − 2 and s_i − 1 at the end of block i − 1. Let us also assume that the relay receiver knows w_i − 1. We shall show that a good choice of {C, S} will allow the receiver to know (w_i − 1, s_i) and the relay receiver to know w_i at the end of block i (with probability of error ≤ ϵ). Thus the information state (w_i − 1, s_i) of the receiver propagates forward, and a recursive calculation of the probability of error can be made, yielding probability of error ≤ Bϵ.

We summarize the use of the code as follows.

Transmission in block i − 1: x₁(w_i − 1|s_i − 1), x₂(s_i − 1).

Received signals in block i − 1: Y₁(i − 1), Y(i − 1) .

Computation at the end of block i − 1: the relay receiver Y₁(i − 1) is assumed to know w_i − 1. The integer w_i − 1 falls in some cell of the partition S. Call the index of this cell s_i. Then the relay is prepared to send x₂(s_i) in block i. Transmitter x₁ also computes s_i from w_i − 1. Thus s_i will furnish the basis for cooperative resolution of the y uncertainty about w_i − 1.

Remark: In the first block, the relay has no information s₁ necessary for cooperation. However any good sequence x₂ will allow the block Markov scheme to get started, and the slight loss in rate in the first block becomes asymptotically negligible as the number of blocks B → ∞.

Transmission in block i: x₁(w_i|s_i), x₂(s_i).

Received signals in block i: y₁(i), y(i).

Computation at end of block i: 1) The relay calculates w_i from y₁(i). 2) The unique jointly typical x₂(s_i) with the received y(i) is calculated. Thus the s_i is known to the receiver. 3) The receiver calculates his ambiguity set J(\mathnormaly(i − 1)) i.e., the set of all w_i − 1 such that (x₁(w_i − 1|s_i − 1), x₂(s_i − 1), y(i − 1)) are jointly ϵ-typical.

The receiver then intersects \strikeout off\uuline off\uwave offJ(\mathnormaly(i − 1)) and the cell S_{s_i}. By controlling the size of J, we shall (1 − ϵ)-guarantee that this intersection has one and only one member- the correct value w_i − 1. We conclude that the receiver y(i) has correctly computed (w_i − 1, s_i) from (w_i − 2, s_i − 1) \strikeout off\uuline off\uwave offЗошто му треба (w_i − 2, s_i − 1)??? and (y(i − 1), y(i)).

We shall use the code as outlined previously in this section. It is important to note that, although Theorem 1 treats degraded relay channels, the proof of achievability of C and all constructions in this section apply without change to arbitrary relay channels. It is only in the converse that degradedness is needed to establish that the achievable rate C is indeed the capacity. the converse is proved in Section III.

We shall now describe the random codes. Fix a probability mass function p(x₁, x₂).

First generate at random M₀ = 2^nR₀ independent identically distributed n-sequences in X^\mathnormaln_\mathnormal2 , each drawn according to p(x₂) = ∏ⁿ_i = 1p(x_2i). Index them as x₂(s), s ∈ [1, 2^nR₀]. For each x₂(s), Ова е многу важно! Сака да каже дека за секоj bin s генерираш посебна кодна подкнига од 2^nR елементи. Вкупната кодна книга содржи 2^nR₀ x2^nR₁ елементи. generate M = 2^nR conditionally independent n-sequences x₁(w|s), w ∈ [1, 2^nR] drawn according to p(x₁|x₂(s)) = ∏ⁿ_i = 1p(x_1i|x_2i(s)). This defines a random code book C\mathnormal = {x₁(w|s), x₂}. Reveal the assignments to both the encoder and the decoder.

Тhe random partition S\mathnormal = {S₁, S₂..., S_2^nR₀} of {1, 2, ..., 2^nR} is defined as follows. Let each integer w ∈ [1, 2^nR] be assigned independently, according to a uniform distribution over the indices s = 1, 2, ..., 2^nR₀, to cell S_s. We shall use the functional notation s(w) to denote the index of the cell in which w lies. Reveal the s(w) assignments to Relay and Destination.

We recall some basic results concerning typical sequences. Let {X⁽¹⁾, X⁽²⁾..., X^(k)} denote a finite collection of discrete random variables with some fixed joint distribution p(x⁽¹⁾, x⁽²⁾, ..., x^(k)), for (x⁽¹⁾, x⁽²⁾, ..., x^(k)) ∈ X⁽¹⁾ xX⁽²⁾ x...xX^{\mathnormal(k)}. Let S denote an ordered subset of these random variables, and consider n independent copies of S. Thus

(19) Pr{S = s} = ⁿ∏_i = 1Pr(S_i = s_i), s ∈ Sⁿ

Let \mathchoiceN(s;s)N(s;s)N(s;s)N(s;s) be the number of indices i ∈ {1, 2, ..., n} such that S_i = s. By the law of large numbers, for any subset S of random variables and for all s ∈ S,

(20) (1)/(n) N(s, s) → p(s)

N(s;s) го замислувам во експеримент на фрлање на коцка како број на пати коцката паѓа на одредена бројка. n го замислувам е колку пати е направен експериментот (фрлање на коцка). За подолу истото го замислуваш за случаен процес кој се состои од секвенца од k коцки.
18.06.14
Внимавај не се работи за секвенца од случајни променливи како гореш што замислувам туку се работи за секвенца од случајни процеси.
Последното замислување е следново. Множеството s е секвенца од секвенци од кое вадиш примерок од n обзервации. (1)/(n)N(s, s) сака да каже дека
количникот од бројот на појавувања на секвенцата s во примерокот од обзервации и вкупната должина на примерокот, стреми кон веројатноста на појавување на секвенцата s.

Also

(21) − (1)/(n)⋅logp(s₁, s₂, ..., s_n) = − (1)/(n) ⁿ⎲⎳_i = 1log(p(s_i)) → H(S)

Convergence in 20↑ and 21↑ takes place simultaneously with probability one for all 2^k subsets

S ⊆ {X⁽¹⁾, X⁽²⁾, ..., X^(k)}

Consider the following definition of joint typicality.

The set A_ϵ of ϵ-typical n-sequences (x⁽¹⁾, x⁽²⁾, ..., x^(k)) is defined by:

A_ϵ(X⁽¹⁾, X⁽²⁾..., X^(k)) = A_ϵ = ⎧⎩(x⁽¹⁾, x⁽²⁾, ..., x^(k)):||(1)/(n)N(x⁽¹⁾, x⁽²⁾, ..., x^(k);x⁽¹⁾, x⁽²⁾, ..., x^(k)) − p(x⁽¹⁾, x⁽²⁾, ..., x^(k))|| <

< ϵ||X⁽¹⁾ xX⁽²⁾ x...xX^{\mathnormal(k)}|| for (x⁽¹⁾, x⁽²⁾, ..., x^(k)) ∈ X⁽¹⁾ xX⁽²⁾ x...xX^{\mathnormal(k)}}

where ||ℛ|| is cardinality of the set ℛ.

Remark: The definition of typicality, sometimes called strong typicality Се потсетив на дефиницијата на strong typicality во EIT Chapter 15.8. can be found in work of Wolfowitz [13] and Berger [12]. Strong typicality implies (week) typicality used in [8], [14]. The distinction is not needed until the proof of Theorem 6 in Section VI of this paper.

The following is a version of the asymptotic equipartition property involving simultaneous constraints [12], [14].

For any ϵ > 0 , there exist and integer n such that A_ϵ(S) satisfies

i) Pr{A_ϵ(S)} ≥ 1 − ϵ, for all S ⊆ {X⁽¹⁾, X⁽²⁾..., X^(k)}

ii) s ∈ A_ϵ(S) ⇒ || − (1)/(n)logp(s) − H(s)|| ≤ ϵ

(22) iii) (1 − ϵ)⋅2^{n(H(S) − ϵ)} ≤ ||A_ϵ(S)|| ≤ 2^{n(H(S) + ϵ)}

We shall need to know the probability that conditionally independent sequences are jointly typical. Let S₁, S₂ and S₃ be three subsets of X⁽¹⁾, X⁽²⁾..., X^(k). Let S^’₁, S^’₂ be conditionally independent given S₃ with the marginals

p(s₁|s₃) = ∑_s₂p(s₁, s₂, s₃) ⁄ p(s₃)

p(s₂|s₃) = ∑_s₁p(s₁, s₂, s₃) ⁄ p(s₃)

The following lemma is provided in [14].

Let (S₁, S₂, S₃) ~ ∏ⁿ_i = 1p(s_1i, s_2i, s_3i) and \strikeout off\uuline off\uwave off(S^’₁, S^’₂, S^’₃) ~ ∏ⁿ_i = 1p(s_1i|s_3i)p(s_2i|s_3i)p(s_3i). Then, for n such that P{A_ϵ(S₁, S₂, S₃)} > 1 − ϵ,

(1 − ϵ)2^{− n⋅(I(S₁;S₂|S₃ + 7⋅ϵ)} ≤ P{(S^’₁, S^’₂, S₃) ∈ A_ϵ(S₁, S₂, S₃)} ≤ 2^{− n⋅(I(S₁;S₂|S₃) − 7ϵ)}

Ова лема мислам ја дава веројатноста некоја друга секвенца да припаѓа на типичното множество. (потсeти се на EIT Theorem 7.6.1 - Joint AEP)
18.06.2014
Да ова е всушност Теоремата 15.2.3 од EIT
Доказот од EIT е:

P{(S₁’, S₂’, S₃’) ∈ A⁽ⁿ⁾_ϵ} = ⎲⎳_{(s₁, s₂, s₃) ∈ A⁽ⁿ⁾_ϵ}p(s₃)p(s₁|s₃)p(s₂|s₃)≐|A⁽ⁿ⁾_ϵ(S₁S₂S₃)|2^{− n(H(S₃)±2ϵ)}2^{− n(H(S₁|S₃)±2ϵ)}2^{− n(H(S₂|S₃)±2ϵ)}

≐2^{n(H(S₁S₂S₃)±ϵ) − n(H(S₃)±ϵ) − n(H(S₁|S₃)±2ϵ) − n(H(S₂|S₃)±2ϵ)}≐2^{− n(I(S₁;S₂|S₃)±6ϵ)}

Повторување од EIT

recall AEP from EIT textbook let: X = Xⁿ₁, Y = Yⁿ₁

2^{− n(H(X, Y) + ϵ)} ≤ p(X, Y) ≤ 2^{− n(H(X, Y) − ϵ)}
1) Pr(p(X, Y) ∈ A⁽ⁿ⁾_ϵ) ≥ 1 − ϵ
2) (1 − ϵ)⋅2^{n(H(X, Y) − ϵ)} ≤ |A⁽ⁿ⁾_ϵ| ≤ 2^{n(H(X, Y) + ϵ)}
3) (1 − ϵ)2^{− n(I(X, Y) + 3ϵ)} ≤ Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) ≤ 2^{− n(I(X, Y) − 3ϵ)}

1 = ⎲⎳_x, yp(X, Y) ≥ ⎲⎳_x, y2^{− n(H(X, Y) + ϵ)} ≥ ⎲⎳_{(x, y) ∈ A⁽ⁿ⁾_ϵ}2^{− n(H(X, Y) + ϵ)} = |A⁽ⁿ⁾_ϵ|⋅2^{− n(H(X, Y) + ϵ)} ⇒ |A⁽ⁿ⁾_ϵ| ≤ 2^{n(H(X, Y) + ϵ)}

1 − ϵ ≤ ⎲⎳_{(X, Y) ∈ A⁽ⁿ⁾_ϵ}p(X, Y) ≤ ⎲⎳_{(X, Y) ∈ A⁽ⁿ⁾_ϵ}2^{− n(H(X, Y) − ϵ)} = |A⁽ⁿ⁾_ϵ|⋅2^{− n(H(X, Y) − ϵ)} ⇒ |A⁽ⁿ⁾_ϵ| ≥ (1 − ϵ)⋅2^{n(H(X, Y) − ϵ)}

\strikeout off\uuline off\uwave off

Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) = ⎲⎳_{(\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ}p(\widetildeX, \widetildeY) = |A⁽ⁿ⁾_ϵ|p(\widetildeX)⋅p(\widetildeY) ≤ 2^{n(H(X, Y) + ϵ)}⋅2^{− n(H(\widetildeX) − ϵ)}⋅2^{− n(H(\widetildeY) − ϵ)} = 2^{n⋅H(X, Y) + nϵ − nH(\widetildeX) + nϵ − nH(\widetildeY) + nϵ}

= 2^{− n⋅( − H(X, Y) + H(\widetildeX) + H(\widetildeY)) + 3nϵ} = 2^{− n⋅( − H(\widetildeY|\widetildeX) + H(\widetildeY)) + 3nϵ} = 2^{− n(I(\widetildeX:\widetildeY) − 3ϵ)} ⇒ Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) ≤ 2^{− n(I(\widetildeX;\widetildeY) − 3ϵ)}

Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) = ⎲⎳_{(\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ}p(\widetildeX, \widetildeY) = ⎲⎳_{(\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ}p(\widetildeX)⋅p(\widetildeY) = |A⁽ⁿ⁾_ϵ|p(\widetildeX)⋅p(\widetildeY) ≥ (1 − ϵ)⋅2^{n(H(X, Y) − ϵ)}⋅2^{− n(H(\widetildeX) + ϵ)}⋅2^{− n(H(\widetildeY) + ϵ)} =

(1 − ϵ)⋅2^{nH(X, Y) − n⋅ϵ − nH(\widetildeX) − n⋅ϵ − nH(\widetildeY) − n⋅ϵ} = (1 − ϵ)⋅2^{− n( − H(X, Y) + H(\widetildeX) + H(\widetildeY)) − 3n⋅ϵ} = (1 − ϵ)⋅2^{− n( − H(\widetildeY|\widetildeX) + H(\widetildeY)) − 3n⋅ϵ} = (1 − ϵ)⋅2^{− n(I(X;Y) + 3⋅ϵ)}

⇒ Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) ≥ (1 − ϵ)⋅2^{− n(I(X;Y) + 3⋅ϵ)} i.e. (1 − ϵ)⋅2^{− n(I(X;Y) + 3⋅ϵ)} ≤ Pr((\widetildeX, \widetildeY) ∈ A⁽ⁿ⁾_ϵ) ≤ 2^{− n(I(\widetildeX;\widetildeY) − 3ϵ)}

Let w_i ∈ [1, 2^nR] be the next index to be sent in block i, and assume that w_i − 1 ∈ S_{s_i}. The encoder then sends x₁(w_i|s_i). The relay has an estimate ŵ̂_i − 1 of the previous index w_i − 1 ∈ S_{s_i}. (This will be made precise in the decoding section.) Assume that ŵ̂_i − 1 ∈ S_{ŝ̂_i}. Then the relay encoder sends the codeword x₂(s_î̂) in block i. Ова е многу важно! Значи релето гледа во којa клетка припаѓа примениот сигнал и врз основ на индексот на таа клетка го праќа содветниот симбол x₂ во наредниот блок.

i 1 2 3 4 ... i ... b X₁ x₁(w₁|s₁) x₁(w₂|s₂) x₁(w₃|s₃) x₁(w₄|s₄) x₁(w_j|s_j) x₁(w_b|s_b) X₂ 0 x₂(s₂) x₂(s₃) x₂(s₄) x₂(s_j) x₂(s_b) Y y(1) y(2) y(3) y(4) y(j) y(b)

We assume that at the end of block (i − 1) the receiver knows (w₁, w₂, ...w_i − 2) and (s₁, s₂, ..., s_i − 1) and the relay knows (w₁, w₂, ...w_i − 1) and consequently \mathchoice(s₁, s₂, ..., s_i)(s₁, s₂, ..., s_i)(s₁, s₂, ..., s_i)(s₁, s₂, ..., s_i).

The decoding procedures at the end of block i are as follows.

\mathchoice1.1.1.1. Knowing s_i, and upon receiving y₁(i), the relay receiver estimates the message of the transmitter w_î̂ = w if there exists a unique w such that (x₁(w|s_i), x₂(s_i), y₁(i)) are jointly ϵ-typical. Using Lemma 2, it can be shown that \mathchoicew_î̂ = w_iw_î̂ = w_iw_î̂ = w_iw_î̂ = w_i with arbitrary small probability of error if

(23) \mathchoiceR < I(X₁;Y₁|X₂)R < I(X₁;Y₁|X₂)R < I(X₁;Y₁|X₂)R < I(X₁;Y₁|X₂)

and n is sufficiently large. Овој израз ја дефинира горната граница на брзината на пренос во каналот!!! Односно изразот R < I(X₁, X₂;Y).

\mathchoice2.2.2.2. The receiver declares that s_î = s was sent if there exist one and only one s such that (x₂(s), Y(i)) are jointly ϵ -typical. From Lemma 2 we know that s_i can be decoded with arbitrary small probability of error if s_i can be decoded with arbitrarily small probability of error if s_i takes on less than 2^nI(X₂;Y) values , i.e. if

(24) \mathchoiceR₀ < I(X₂;Y)R₀ < I(X₂;Y)R₀ < I(X₂;Y)R₀ < I(X₂;Y)

and n is sufficiently large.

\mathchoice3.3.3.3. Assuming that s_i is decoded successfully at the receiver, then ŵ_i − 1 = w is declared to be the index sent in bloc i − 1 if there is a unique \mathchoicew ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1))w ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1))w ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1))w ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1)). It will be shown that if n is sufficiently large and if

(25) \mathchoiceR < I(X₁;Y|X₂) + R₀R < I(X₁;Y|X₂) + R₀R < I(X₁;Y|X₂) + R₀R < I(X₁;Y|X₂) + R₀

then \mathchoiceŵ_i − 1 = w_i − 1ŵ_i − 1 = w_i − 1ŵ_i − 1 = w_i − 1ŵ_i − 1 = w_i − 1 with arbitrary small probability of error.

Претпоставувам дека ℒ(y(i-1)) функцијата за декодирање (decoding function - g(...)) која го дава излезниот симбол во приемникот. Да ама излезот од оваа функција е множество. Подолу има формула за кардиналност на тоа множество. Веројатно го дава множеството на можни излезни симболи.
25.06.2014
Накратко сакам да ја опишам целата постапка како функционира релејниот систем и како се остварува кооперацијата.
Имаш w ∈ [1, ..., 2^nR] пораки односно Xⁿ(w) кодни зборови кои сакаш да ги пренесеш. Прво ги складираш случајно во 2^nR₀ кошнички. Ако бројот на кошнички е доволно голем можеш да очекуваш во секоја кошничка да има само еден типичен коден збор. Со тоа ја формираш коднага книга x(w|s(w)). Кодната книга ја соопштуваш на релето и дестинацијата. Кога ќе го испратиш еден кодниот зборо x₁(w_i − 1|s_i) тој се декодира во релето и во дестинацијата. Релето е поблиску до изворот од дестинацијата и затоа неговата естимација на овој симбол е поточна (посигурна) од естимациајта во дестинацијата. Со други зборови на дестинацијата и е потребна дополнителна информација за да со поголема сигурност го реконструира испратениот коден збор. Таа дополнителна информација ќе ја добие во наредниот блок кога изворот ќе го испрати x₁(w_i|s_i + 1). Во меѓувреме релето го реконструирал w_i − 1 (ŵ̂_i − 1)од приемениот деградиран x₁(w_i − 1|s) т.е. од y₁ (гледа во претходно дистрибуираната кодна книга), а дестинацијата врз основ на деградиранот x₁(w_i − 1|s_i) т.е y₂ го идентивикува множеството на можни кодни зборови ℒ(y(i − 1)). Кога изворот ќе го прати x₁(w_i|s_i + 1) тогаш релето ќе го прати x₂(s_i). Дестинацијата врз основ на x₂(ŝ̂_i) ќе го реконструира ŝ_i т.е. ќе ја естимира коншничката каде припаѓал w_i − 1. Во кошничката може да припаѓаат повеќе кодни зборови. Пресекот меѓу кошничката и множеството на можни кодни зборови: S_{s_i}∩ℒ(y(i − 1)) ќе ја дате точната естимација на испратената порака w_i − 1.

Гледаш во i-от тајмслот приемникот го декодира w_i − 1, a предаватеот всушност го пратил w_i, Ова w_i е наменето за релето за да тоа го најде s_i + 1 кое ќе го прати како x(s_i + 1) во наредниот тајмслот кога предавателот ќе испраќа x(w_i + 1|s_i + 1) .

Заттоа вкупната информација е R ≈ I(X₁;Y|X₂) + R₀ ја сумираш информацијата пратена од изворот до релето во претходниот слот и информацијата пратена од релето кон приемникот во сегашниот слот.
30.07.2014
Не е баш вака ова е сума од информацијата од изворот до релето и информацијата од изворот до дестинацијата.

Thus combining 24↑ and 25↑ yields R < I(X₁, X₂;Y) (R < I(X₁;Y|X₂) + R₀ < I(X₁;Y|X₂) + I(X₂;Y) = I(X₁, X₂;Y)) , the first term in the capacity expression in Theorem 1. The second term is given by constraint 23↑.

For the above scheme, we will declare an error in block i if one or more of the following events occurs.

E_0i (x₁(w_i|s_i), x₂(s_i), y₁(i), y(i)) is not jointly ϵ-typical.

E_1i in decoding step 1, there exists w̃ ≠ w_i such that x₁((w̃|s_i), x₂(s_i), Y₁(i)) is jointly typical. Сака да каже дека не постои unique w.

E_2i in decoding step 2, there exist s̃ ≠ s_i such that (x₂(s̃), y(i)) is jointly typical. Сака да каже дека постои и друго s = s̃ така што (x₂(s̃), Y(i)) се jointly typical.

E_3i decoding step 3 fails. Let E_3i = E^’_3i∪E^’’_3i , where

E^’_3i w_i − 1∉S_{s_i}∩ℒ\mathnormal(y(i − 1)) Сака да каже дека не може да се најде такво w такаш што w ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1)).

E^’’_3i there exists w̃ ∈ [1, 2^nR], w̃ ≠ w_i − 1, such that w̃ ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1)). Сака да каже дека постои и другo w = w̃ за кое што исто така важи w̃ ∈ S_{s_i}∩ℒ\mathnormal(y(i − 1)) .

Now we bound the probability of error over the B n-blocks. Let \mathchoiceW = (W₁, W₂, .., W_B − 1, ∅)W = (W₁, W₂, .., W_B − 1, ∅)W = (W₁, W₂, .., W_B − 1, ∅)W = (W₁, W₂, .., W_B − 1, ∅) be the transmitted sequence of indices. We assume the indices W_i are independent identically distributed random variables uniformly distributed on [1, 2^nR] . The relay estimates W to be \mathchoiceŴ̂ = (Ŵ̂₁, Ŵ̂₂, ...Ŵ̂_B − 1, ∅)Ŵ̂ = (Ŵ̂₁, Ŵ̂₂, ...Ŵ̂_B − 1, ∅)Ŵ̂ = (Ŵ̂₁, Ŵ̂₂, ...Ŵ̂_B − 1, ∅)Ŵ̂ = (Ŵ̂₁, Ŵ̂₂, ...Ŵ̂_B − 1, ∅). The receiver estimates \mathchoiceŜ = (∅, Ŝ₂, Ŝ₃, ...Ŝ_B)Ŝ = (∅, Ŝ₂, Ŝ₃, ...Ŝ_B)Ŝ = (∅, Ŝ₂, Ŝ₃, ...Ŝ_B)Ŝ = (∅, Ŝ₂, Ŝ₃, ...Ŝ_B) and \strikeout off\uuline off\uwave off\mathchoiceŴ = (∅, Ŵ₁, Ŵ₂, .., Ŵ_B − 1)Ŵ = (∅, Ŵ₁, Ŵ₂, .., Ŵ_B − 1)Ŵ = (∅, Ŵ₁, Ŵ₂, .., Ŵ_B − 1)Ŵ = (∅, Ŵ₁, Ŵ₂, .., Ŵ_B − 1). Define the error events F_i for \uuline default\uwave defaultdecoding errors in block i\strikeout off\uuline off\uwave off by:

(26) \mathchoiceF_i = {Ŵ̂_i ≠ W_i or Ŵ_i ≠ W_{\mathchoicei − 1i − 1i − 1i − 1} or S_î ≠ S_i} = ∪³_k = 0E_{k_i}F_i = {Ŵ̂_i ≠ W_i or Ŵ_i ≠ W_{\mathchoicei − 1i − 1i − 1i − 1} or S_î ≠ S_i} = ∪³_k = 0E_{k_i}F_i = {Ŵ̂_i ≠ W_i or Ŵ_i ≠ W_{\mathchoicei − 1i − 1i − 1i − 1} or S_î ≠ S_i} = ∪³_k = 0E_{k_i}F_i = {Ŵ̂_i ≠ W_i or Ŵ_i ≠ W_{\mathchoicei − 1i − 1i − 1i − 1} or S_î ≠ S_i} = ∪³_k = 0E_{k_i}.

19.06.14

Дури сега во суштина ја сконтав 26↑ и зошто само Ŵ ≠ W_{\mathchoicei − 1i − 1i − 1i − 1}. Види ги подвлекувањата во црвено. Тие всушност го потврдуваат она што го кажав во 13↑

Се ми се чини дека треба наместо F_i овде да биде F_i − 1. Не, не, не со F^c_i − 1 во наредните изрази сака да исклучи дека во претходниот блок се случила грешка.

\strikeout off\uuline off\uwave off \strikeout off\uuline off\uwave offНе знам што значи индексот „c”. Претпоставив, а потоа и видов потврда на yahoo answers дека се работи за негација т.е. комплемент.

Да така е ов EIT Chapter 15 постојано ја користи таа нотација.

We have argued in encoding-decoding steps 1 and 2 that: негација од дисјункција е конјукција од негациите (de morgan law).

(27) P(E_0i|F^c_{\mathchoicei − 1i − 1i − 1i − 1}) ≤ (ϵ)/(4B)

Ова е логично негација од 26↑ согласно законот на de morgan вели дека \strikeout off\uuline off\uwave offŴ̂_i − 1 = W_i − 1 and Ŵ_i − 1 = W_i − 2 and Ŝ_i − 1 = S_i − 1 (негација од дисјункција е конјукција од поединечните негации.). Од друга страна тоа значи дека\uuline default\uwave default (x₁(w|s_i), x₂(s_i), y₁(i)) се jointly ϵ-typical што е спротивно на E_0i.

Зошто дели со 4B???

(28) P(E_1i∩E^c_0i|F^c_{\mathchoicei − 1i − 1i − 1i − 1}) ≤ (ϵ)/(4B)

Сака да каже дека штом \strikeout off\uuline off\uwave offимаме настанE^c_0i\uuline default\uwave default кој вели дека не е точно дека \strikeout off\uuline off\uwave off(x₁(w_i|s_i), x₂(s_i), y₁(i), y(i)) не се типични од една страна и од друга страна настан (F^c_i − 1) кој вели дека се случило Ŵ̂_i − 1 = W_i − 1 and Ŵ_i − 1 = W_i − 2 and Ŝ_i − 1 = S_i − 1 тогаш веројатност да се случи настан (E_1i) \uuline default\uwave defaultw̃ ≠ w_i така што (x₁(w̃|s_i), x₂(s_i), Y₁(i)) се здружено типични е многу мала. Слично е и толкувањето за 29↓.

(29) P(E_2i∩E^c_0i|F^c_{\mathchoicei − 1i − 1i − 1i − 1}) ≤ (ϵ)/(4B)

Малку ме бунат сините (cyan) индексите ама и со нив е ОК толкувањето. E настаните се за сегашниот тајмслот, а F настаните за претхондиот.

We now show that \strikeout off\uuline off\uwave offP(E_3i∩E^c_2i∩E^c_0i|F^c_i − 1) can be made small.

If

\mathchoiceR < I(X₁;Y|X₂) + R₀ − 7ϵR < I(X₁;Y|X₂) + R₀ − 7ϵR < I(X₁;Y|X₂) + R₀ − 7ϵR < I(X₁;Y|X₂) + R₀ − 7ϵ,

then for sufficiently large n

(30) P(E_3i∩E^c_2i∩E^c_0i|F^c_i − 1) ≤ (ϵ)/(4B)

\mathchoiceProof:Proof:Proof:Proof:First we bound E{||L\mathnormal(Y(i − 1))|||\mathnormalF^c_i − 1}, where ||ℒ|| denotes the number of elements in ℒ. Let

(31) ψ(w|y(i − 1)) = ⎧⎨⎩ 1 (x₁(w|s_i − 1), x₂(s_i − 1), y(i − 1)) is jointly typical, 0 otherwise.

The cardinality of L\mathnormal(y(i − 1)) is the random variable

(32) ||L\mathnormal(y(i − 1))|| = ⎲⎳_wψ(w|y(i − 1))

and

E{||ℒ\mathnormal(y(i − 1))|||\mathnormalF^c_i − 1} = \mathchoiceE{ψ(w_i − 1|y(i − 1))|F^c_i − 1}E{ψ(w_i − 1|y(i − 1))|F^c_i − 1}E{ψ(w_i − 1|y(i − 1))|F^c_i − 1}E{ψ(w_i − 1|y(i − 1))|F^c_i − 1} + \mathchoice⎲⎳_{w ≠ w_i − 1}E{ψ(w|y(i − 1))|F^c_i − 1}⎲⎳_{w ≠ w_i − 1}E{ψ(w|y(i − 1))|F^c_i − 1}⎲⎳_{w ≠ w_i − 1}E{ψ(w|y(i − 1))|F^c_i − 1}⎲⎳_{w ≠ w_i − 1}E{ψ(w|y(i − 1))|F^c_i − 1}

From Lemma 2 we obtain, for each w ∈ [1, M],

(33) E{ψ(w|y(i − 1))|F^c_i − 1} ≤ 2^{− n(I(X₁;Y|X₂) − 7ϵ)} w≠w_i − 1

(Веројатноста некоја друга секвенца да припаѓа на типилното множество е мала)

Therefore (by introducing 33↑ in 32↑)

E{||ℒ\mathnormal(y(i − 1))|||\mathnormalF^c_i − 1} ≤ \cancelto зеленото од Eq341 + \cancelto портокаловото од Eq34(2^nR − 1)⋅(2^{− n(I(X₁;Y|X₂) − 7ϵ)}) = 1 + 2^nR⋅2^{− n(I(X₁;Y|X₂) − 7ϵ)} − 2^{− n(I(X₁;Y|X₂) − 7ϵ)} ≤ 1 + 2^{n⋅(R − I(X₁;Y|X₂) + 7ϵ)}

The event F^c_i − 1 implies that w_i − 1 ∈ L\mathnormal(y(i − 1)). Also E^c_2i ⇒ ŝ_i = s_i ⇒ w_i − 1 ∈ S_{s_i}. Thus

(34) P(E^’_3i∩E^c_2i∩E^c_0i|F^c_i − 1) = 0

E^’_3i вели дека се случил настанот \strikeout off\uuline off\uwave offw_i − 1∉S_{s_i}∩ℒ\mathnormal(y(i − 1)) што е во контрадикција со горното тврдење. Затоа веројатноста тој настан да се случи во вакви услови е 0.\uuline default\uwave default

Hence

P(E_3i∩E^c_2i∩E^c_0i|F^c_i − 1) = P(E^’’_3i∩E^c_2i∩E^c_0i|F^c_i − 1) ≤ P{there exists w ≠ W_i − 1such that w ∈ ℒ\mathnormal(y(i − 1)∩S_{s_i}|F^c_i − 1)} ≤

≤ E{⎲⎳_{\oversetw ≠ W_i − 1w ∈ ℒ\mathnormal(y(i − 1))}P(w ∈ S_{s_i})|F^c_i − 1} ≤ E{||ℒ\mathnormal(y(i − 1))||⋅2^− nR₀|F^c_i − 1} ≤ |\undersetВеројатностанекојадругасеквенцадаприпаѓанатипилнотомножествоемалаПретпоставувам дека P(w ∈ S_{s_i}) = (1)/(2^nR₀)|

= 2^− nR₀⋅E{||ℒ\mathnormal(y(i − 1))|||F^c_i − 1} ≤ | introduce Eq.35| ≤ 2^− nR₀⋅{1 + 2^{n⋅(R − I(X₁;Y|X₂) + 7ϵ)}}

Thus, if \mathchoiceR₀ > R − I(X₁;Y|X₂) + 7⋅ϵR₀ > R − I(X₁;Y|X₂) + 7⋅ϵR₀ > R − I(X₁;Y|X₂) + 7⋅ϵR₀ > R − I(X₁;Y|X₂) + 7⋅ϵ then for sufficiently large n, P(E_3i∩E^c_2i∩E^c_0i|F^c_i − 1) ≤ (ϵ)/(4B). Proof of the lemma But from 24↑ we required: \mathchoiceR₀ < I(X₂;Y)R₀ < I(X₂;Y)R₀ < I(X₂;Y)R₀ < I(X₂;Y).

Combining the two constraints, R₀ drops out, leaving

(35) I(X₂;Y) > R − I(X₁;Y|X₂) + 7⋅ϵ R < I(X₂;Y) + I(X₁;Y|X₂) − 7⋅ϵ = I(X₁, X₂;Y) − 7ϵ ⇒ \mathchoiceR < I(X₁, X₂;Y) − 7ϵR < I(X₁, X₂;Y) − 7ϵR < I(X₁, X₂;Y) − 7ϵR < I(X₁, X₂;Y) − 7ϵ

.

The probability of error is given by

(36) P(W ≠ Ŵ) ≤ P(∪^B_i = 1F_i) = |не разбирам од каде го добива| = P(∪^B_i = 1 { F_i-∪^i − 1_j = 1F_j} )

(37) \overset(a) = ^B⎲⎳_i = 1P{F_i∩F^c₁∩F^c₂...∩F^c_i − 1} ≤ ^B⎲⎳_i = 1P{F_i∩F^c_i − 1}.

Обичната унија ја разбирам. Имено вели грешка се случува или во блокот i = 1 или во i = 2 или ... или во i = B. Ова со одземањето под знакот на унијата не го контам!? Можеби треба да бидеF^c_j. Сепак конјукциите во (а) ги контам вака. Веројатноста на грешка во i-от интервал, подразбира дека се случил настанот F_i. Сите претхонди (во претходните слотови) настани се со негација т.е не се случиле.
P(A∪B∪C) = P(A∪B) + P(C) − P((A∪B)∩C) = P(A) + P(B) − P(A∩B) + P(C) − P((A∪B)∩C) = P(A) + P(B) + P(C) − P(A∩B) − P((A∪B)∩C)

\strikeout off\uuline off\uwave off\mathnormal∪³_i = 1 { F_i-∪^i − 1_j = 1F_j} = \cancelF₁ + \cancelF₂ − \cancelF₁ + F₃ − F₁ − \cancelF₂ = F₃ − F₁

24.06.14
Дефинитивно минусот мислам дека значи негација!!!!

But:

(38) {F_i∩F^c_i − 1} = ∪³_k = 0E_ki∩F^c_i − 1

Thus,

{F_i∩F^c_i − 1} = ³⎲⎳_k = 0 {E_ki − ∪^k − 1_m = 1E_m}∪F^c_i − 1 ≤ ³⎲⎳_k = 0P({E_ki∩E^c_0i...∩E^c_{(k − 1)i}}|F^c_i − 1).

The conditional probabilities of error are bounded by:

P(E_ki∩E^c_0i...∩E^c_{(k − 1)i}|F^c_i − 1) ≤ (ϵ)/(4B).

Thus

(39) P(Ŵ ≠ W) ≤ ϵ

This concludes the proof of Lemma 3.

It is now standard procedure to argue that there exists a code C^* such that P(W ≠ Ŵ|C^*) ≤ ϵ. Finally, by throwing away the worst half of the w in {1, ...2^nR}^B − 1 and re-indexing them, we have the maximal error

(40) P(Ŵ = w_i|C^*, w_i) ≤ 2ϵ, for i ∈ [1, 2^{nR(B − 1) − 1}].

Thus for ϵ > 0, and n sufficiently large,

(41) λ_n ≤ 2ϵ for rates R̃ = (nR(B − 1) − 1)/(nB)where R < C.

Во формулта 41↑ се јавува n затоа што капацитетот т.е. брзината ја изразува во симболи(бити)/трансмисија, а не пораки/трансмисија. Бројот на различни симболи е 2^nR а бројот на различни пораки е B − 1

Ова е многу слично на доказот за Achievability на Channel Coding Theorem 7.7.1 од EIT.

First letting n → ∞, then B → ∞ , and finally ϵ → 0 , we see that R < C is achievable. Thus the achievability of C in theorem 1 is proved.

First we show that for the general (not necessarily degraded) relay channel an upper bound to the capacity C is given by

(42) C ≤ sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}.

Многу е поедноставен доказот во Network Information Theory од El Gamal

If

\mathchoiceR > sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}R > sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}R > sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}R > sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}

Овaa теорема ја дефинира долната граница на брзината на пренос во каналот!!!

then there exists λ > 0 such that P_n(e) > λ for all n. Before proving Theorem 4, we note that this theorem can be specialized to give the converses to Theorems 1, 2, and 3.

For the degraded relay channel

\strikeout off\uuline off\uwave off

C ≤ sup_{p(x₁, x₂)}min{I(X₁, X₂;Y), I(X₁;Y₁|X₂)}

It follows from degradedness assumption 10↑ that

\strikeout off\uuline off\uwave offp(y, y₁|x₁, x₂) = p(y₁|x₁, x₂)⋅p(y|y₁, x₂)

thus rendering the upper bound in Theorem 4 and the bound in Corollary 1 equal.

The reversely degraded relay channel has capacity

C₀ ≤ max_p(x₁)max_x₂{I(X₁;Y|x₂)}

Proof: Reverse degradation 11↑ implies in Theorem 4 that

p(y, y₁|x₁, x₂) = p(y|x₁, x₂)⋅p(y₁|y, x₂),

\strikeout off\uuline off\uwave offX₁ → (X₂, Y) → Y₁

Also, the second term in the brackets is always less than the first:

I(X₁, X₂;Y) ≥ I(X₁;Y|X₂) = I(X₁;Y, Y₁|X₂)

I(X₁, X₂;Y) = I(X₂;Y) + I(X₁;Y|X₂) ≥ I(X₁;Y|X₂)

Finally,

C₀ ≤ sup_{p(x₁, x₂)}I(X₁;Y|X₂) = max_x₂max_p(x₁)I(X₁;Y|x₂)

since I is linear in p(x₂), and p_x₂(.) takes values in a simplex. Thus I is maximized at an extreme point. Q.E.D.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions, a k-simplex is a k-dimensional polytope which is the convex hull of its k + 1 vertices. More formally, suppose the k + 1 points u₀, ..., u_k ∈ ℜ^k are affinely independent, which means, u₁ − u₀, ..., u_k − u₀ are linearly independent. Then, the simplex determined by them is set of points
C = {θ₀u₀ + ... + θ_ku_k|θ ≥ 0, 0 ≤ i ≤ k, ∑^k_i = 0θ_i = 1}
For example, a 2-simplex is a triangle, a 3 simplex is a tetrahedron. A single point may be considered a 0-simplex, and a line segment may be considered, a 1-simplex.
C = {θ₀u₀ + θ₁u₁}

Од Wikipedia categorical distribution.

Мислам дека Cover со горното тврдење сака да каже дека p(X₂) е дискретна дистрибуција и дека вредностите и веројатностите може така да се подредат така што се добива линеарна дистрибуција. Сеедно е дали изводот во Lagrange Multipliers е по p_i или по i.
I(X₁;Y|X₂) = H(Y|X₂) − H(Y|X₁X₂) = ∑_p(x₂)p(x₂)H(Y|X₂ = x₂) + ∑_p(x₂)p(x₂)H(Y|X₁, X₂ = x₂)
Линеарноста потекнува од таму што p(x₂) ги множи ентропиите во горниот израз. Се едно е дали во производот ќе стои p(x₂) или само x₂ кога ќе пресметуваш максимум со лагранжови множители.

Given any (M, n) code fort the relay channel, the probability mass function on the joint ensemble W, X₁, X₂, Y, Y₁ is given by:

(43) p(w, x₁, x₂, y, y₁) = \oversetp(w)(1)/(M)⋅p(x₁|w)⋅ⁿ∏_i = 1p(x_2i|y₁₁, ..., y_1i − 1)⋅p(y_i, y_1i|x_1i, x_2i)

Ова не успеав да го докажам во целост!?

Consider the identity

nR = H(W) = I(W;Y) + H(W|Y)

By Fano’s inequality

(44) H(W|Y) ≤ 1 + P_n(e)nR\overset△ = nδ_n

Thus

(45) nR ≤ I(W;Y) + nδ_n

nR ≤ H(W) = I(W;Y) + H(W|Y) = I(W;Y) + nδ_n

We now upper bound I(W;Y) in a lemma that is essentially similar to Theorem 10.1 in [1].

(46) i) I(W;Y) ≤ ⁿ⎲⎳_i = 1I(X_1i, X_2i;Y_i)

(47) ii) I(W;Y) ≤ ⁿ⎲⎳_i = 1I(X_1i;Y_1i, Y_i|X_2i).

Proof: To simplify notation, we shall use Yⁱ = (Y₁, Y₂, ...Y_i) throughout the rest of this paper. First considering i), we apply the chain rule to obtain.

I(W;Y) = ⁿ⎲⎳_i = 1I(W;Y_i|Y^i − 1) = ⁿ⎲⎳_i = 1(H(Y_i|Y^i − 1) − H(Y_i|Y^i − 1, W)) ≤

(48) ⁿ⎲⎳_i = 1(H(Y_i) − H(Y_i|Y^i − 1, W))\overset(a) ≤ ⁿ⎲⎳_i = 1(H(Y_i) − H(Y_i|X_1iX_2iY^i − 1, W)).

(a) во последното неравенство користи conditioning reduces entropy.

By discrete memorylessness of the channel, Y_i and (W, Y^i − 1) are conditionaly independent given (X_1i, X_2i).

I(W;Y) ≤ ⁿ⎲⎳_i = 1(H(Y_i) − H(Y_i|X_1iX_2i)) = ⁿ⎲⎳_i = 1I(X_1i, X_2i;Y_i)

Considerig ii) we have

I(W;Y) ≤ I(W;Y, Y₁) = I(W;Y) + I(W;Y₁|Y) = ⁿ⎲⎳_i = 1I(W;Y_i, Y_1i|Y^i − 1Y^i − 1₁) = ⁿ⎲⎳_i = 1H(W|Y^i − 1Y^i − 1₁) − H(W|Y_i, Y_1i, Y^i − 1, Y^i − 1₁)

(49) = ⁿ⎲⎳_i = 1H(W|Y^i − 1Y^i − 1₁) − H(W|Yⁱ, Yⁱ₁)

It is easy to see that W and X_2i are conditionally independent given (Y^i − 1, Y^i − 1₁). Претпоставувам се работи за марков ланец т.е. деградиран релеен канал каде W → (Y, Y₁) → X₂ Hence

and continuing the sequence of upper bounds in 49↑, we have

I(W;Y) ≤ ⁿ⎲⎳_i = 1H(W|Y^i − 1Y^i − 1₁, X_2i) − H(W|Yⁱ, Yⁱ₁, X_2i) = ⁿ⎲⎳_i = 1I(W;Y_i, Y_1i|Y^i − 1₁Y^i − 1X_2i) =

Не контам зошто ова во жолтово го менува со X_1i? Можеби заради дефиницијата 43↑?

19.06.2014
(d) следи од следниве неравенсттва
∑ⁿ_i = 1H(Y_i, Y_1i|Y^i − 1₁Y^i − 1X_2i) − H(Y_i, Y_1i|W, Y^i − 1₁Y^i − 1X_2i) ≤ ∑ⁿ_i = 1H(Y_i, Y_1i|Y^i − 1₁Y^i − 1X_2i) − H(Y_i, Y_1i|W, Y^i − 1₁Y^i − 1X_1iX_2i) ≤ (*)

Слично како во 48↑ од фактот дека се работи за дискретен канал без меморија, Y_iY_1i не зависат од Y^i − 1Y^i − 1₁ ниту зависат од W ако се дадени (X_1i, X_2i).

And Lemma 4 is proved.

From 45↑ and Lemma 4 it follows that

R ≤ min⎧⎩(1)/(n)ⁿ⎲⎳_i = 1I(X_1i, X_2i;Y_i), (1)/(n)ⁿ⎲⎳_i = 1I(X_1i;Y_1i, Y_i|X_2i)⎫⎭ + δ_n

19.06.14

Од Лема 4 се гледа дека I(W;Y) е помало и од ∑ⁿ_i = 1I(X_1i, X_2i;Y_i) и од ∑ⁿ_i = 1I(X_1i;Y_1i, Y_i|X_2i) логично дека ако ги ставиш во операција min дека повторно I(W;Y) ќе биде помало од нив. На тој начин ги прави минимумите во теоремите 1, 2 и 3. . Мислам дека ова изведување е убаво и може да влезе во Докторската.

We now eliminate the variable n by simple artifice. Let Z be random variable independent of X₁X₂, Y, Y₁ taking values in the set {1, ...n}with probability:

(51) p(Z = i) = (1)/(n) 1 ≤ i ≤ n.

Set

X₁≜X_1Z, X₂≜X_2Z, Y≜Y_Z Y₁≜Y_1Z

Then

(1)/(n)ⁿ⎲⎳_i = 1I(X_1i, X_2i;Y_i) = I(X₁, X₂;Y|Z) ≤ I(X₁, X₂;Y)

Ова е класичен пристап за time sharing што на пример Cover го користи во Главата 15.3 за multiple access channel. Таму го имам и елеганто докажано.

потсетување за ентропија на disjoint mixture
p(X₁) = {p₁, p₂...p_n} p(X₂) = {q₁, q₂...q_n} θ = f(X) = ⎧⎨⎩ 1 with probability p(X = X₁) = α 2 with probability p(X = X₂) = 1 − α
H(θ, X) = H(θ) + H(X|θ) = H(X) + \cancelto0H(θ|X) ⇒ H(X) = H(θ) + H(X|θ) = H(α) + p(θ = 0)⋅H(X|θ = 0) + p(θ = 1)⋅H(X|θ = 1)
= H(α) + α⋅H(X|θ = 0) + (1 − α)⋅H(X|θ = 1) = H(α) + α⋅H(p) + (1 − α)⋅H(q)
Ова може да се генерализира за повеќе од 2 индекси т.е. disjoint mixtures.
Потсетување на тотална експектација
E- коцката паднала на парен број
E(X|E) = 2⋅(1)/(3) + 4⋅(1)/(3) + 6⋅(1)/(3) = 4
E(X|E) = 1⋅(1)/(3) + 3⋅(1)/(3) + 5⋅(1)/(3) = 3
E(X) = p(E)⋅E(X|E) + p(E)⋅E(X|E) = 4 ⁄ 2 + 3 ⁄ 2 = 7 ⁄ 2
(1 + 2 + 3 + 4 + 5 + 6)/(6) = (7)/(2)

Доказ на изразот:
(1)/(n)∑²_i = 1I(X_1iX_2i;Y_i) = \cancelto(1)/(2)p(Z = 1)⋅I(X₁₁X₂₁;Y₁) + \cancelto(1)/(2)p(Z = 2)⋅I(X₁₂X₂₂;Y₂)
\mathchoiceI(X²₁X²₂;Y²|Z)I(X²₁X²₂;Y²|Z)I(X²₁X²₂;Y²|Z)I(X²₁X²₂;Y²|Z) = H(X₁₁, X₁₂X₂₁, X₂₂|Z) − H(X₁₁X₁₂X₂₁, X₂₂|Y₁Y₂, Z) = p(Z = 1)⋅H(X²₁X²₂|Z = 1) + p(Z = 2)H(X²₁X²₂|Z = 2)
− p(Z = 1)⋅H(X²₁X²₂|Y², Z = 1) − p(Z = 2)⋅H(X²₁X²₂|Y², Z = 2) = p(Z = 1)⋅H(X₁₁X₂₁) + p(Z = 2)⋅H(X₁₂X₂₂)
− p(Z = 1)⋅H(X₁₁X₂₁|Y₁) − p(Z = 2)⋅H(X₁₂X₂₂|Y₂) = p(Z = 1)⋅I(X₁₁X₂₁;Y₁) + p(Z = 2)⋅I(X₁₂, X₂₂;Y₁₂) = \mathchoice(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i) n = 2
Треба да го докажам и со користење на:

\strikeout off\uuline off\uwave offZ → (X₁X₂) → (Y, Y₁)

\strikeout off\uuline off\uwave off = p(Z = 1)⋅H(Y₁) + p(Z = 2)⋅H(Y₂) − p(Z = 1)⋅H(Y₁|X₁₁X₂₁) − p(Z = 2)⋅H(Y₂|X₁₂X₂₂) = \mathchoice(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i)(1)/(n)∑ⁿ_i = 1I(X_1i, X₂₁;Y_i) n = 2

19.06.2014
Мислам дека доказот во EIT Chapter 15.3.4 Notebook-т е поедноставен.

by the Markovian relation \mathchoiceZ → (X₁X₂) → (Y, Y₁)Z → (X₁X₂) → (Y, Y₁)Z → (X₁X₂) → (Y, Y₁)Z → (X₁X₂) → (Y, Y₁) induced by channel and the code. Similarly:

(1)/(n)ⁿ⎲⎳_i = 1I(X_1i;Y_i, Y_1i|X_2i) = I(X₁;Y, Y₁|X₂, Z) ≤ I(X₁;Y, Y₁|X₂)

Thus

\mathchoiceR ≤ min{I(X₁, X₂;Y₁), I(X₁;Y, Y₁|X₂)} + δ_nR ≤ min{I(X₁, X₂;Y₁), I(X₁;Y, Y₁|X₂)} + δ_nR ≤ min{I(X₁, X₂;Y₁), I(X₁;Y, Y₁|X₂)} + δ_nR ≤ min{I(X₁, X₂;Y₁), I(X₁;Y, Y₁|X₂)} + δ_n

and Theorem 4 is proved.

Овој доказ е едноставен и добар. Може да влезе во PhD, без делот за achievability. Логично е зошто за да го определи капацитетот бара од овој израз потоа supremum по p(x₁, x₂). Затоа што капацитетот е супремум од сите достигливи брзини на пренесување.

Suppose a transmitter x₁ with power P₁ sends a signal intended for receiver y. However this signal is also received by a relay y₁ that is perhaps physically closer to x₁ than is to y. Transmissions are corrupted by additive Gaussian noise. How can the relay x₂ make good use of y₁ to send a signal at power P₂ that will add to the signal received by the ultimate receiver y?

First we define the model for discrete time additive white Gaussian noise degraded relay channel as shown in 4↓.

Figure 4 Degraded Gaussian relay channel

Let Z₁ = (Z₁₁, ..., Z_1n) be a sequence of independen identically distributed (i.i.d) normal random variables (r.v.’s) with mean zero and variance N₁, and let Z₂ = (Z₂₁, ..., Z_2n) be i.i.d normal r.v.’s independent of Z₁ with mean zero and variance N₂. Define N = N₁ + N₂. At the i-th transmission the real number x_1i and x_2i are sent and:

\mathchoicey_1i = x_1i + z_1iy_1i = x_1i + z_1iy_1i = x_1i + z_1iy_1i = x_1i + z_1i

\mathchoicey_i = x_2i + y_1i + z_iy_i = x_2i + y_1i + z_iy_i = x_2i + y_1i + z_iy_i = x_2i + y_1i + z_i

are received. Thus the channel is degraded \strikeout off\uuline off\uwave offp(y, y₁|x₁, x₂) = p(y₁|x₁, x₂)⋅p(y|y₁, x₂) сака да каже дека y не зависи од x₁ ако се дадени (y₁, x₂) .

Let the message power constraint on the transmitted power be:

(52) \mathchoice(1)/(n)ⁿ⎲⎳_i = 1x²_1i(w) ≤ P₁ w ∈ {1, 2, ...M}(1)/(n)ⁿ⎲⎳_i = 1x²_1i(w) ≤ P₁ w ∈ {1, 2, ...M}(1)/(n)ⁿ⎲⎳_i = 1x²_1i(w) ≤ P₁ w ∈ {1, 2, ...M}(1)/(n)ⁿ⎲⎳_i = 1x²_1i(w) ≤ P₁ w ∈ {1, 2, ...M}

and

(53) \mathchoice(1)/(n)ⁿ⎲⎳_i = 1x²_2i(y₁₁, y₁₂, ..., y_1i − 1) ≤ P₂ (y₁₁, ...y_1n) ∈ ℜⁿ(1)/(n)ⁿ⎲⎳_i = 1x²_2i(y₁₁, y₁₂, ..., y_1i − 1) ≤ P₂ (y₁₁, ...y_1n) ∈ ℜⁿ(1)/(n)ⁿ⎲⎳_i = 1x²_2i(y₁₁, y₁₂, ..., y_1i − 1) ≤ P₂ (y₁₁, ...y_1n) ∈ ℜⁿ(1)/(n)ⁿ⎲⎳_i = 1x²_2i(y₁₁, y₁₂, ..., y_1i − 1) ≤ P₂ (y₁₁, ...y_1n) ∈ ℜⁿ

for transmitted signal x₁ = (x₁₁, ..., x_1n) and relay signal x₂ = (x₂₁, ..., x_2n) respectively.

The definition of a code for this channel is the same as given in section I with the additional constraints in 52↑.

The capacity C^* of the Gaussian degraded relay channel is given by:

(54) \mathchoiceC^* = max_{0 ≤ α ≤ 1}min⎧⎩C⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠, C⎛⎝(αP₁)/(N₁)⎞⎠⎫⎭C^* = max_{0 ≤ α ≤ 1}min⎧⎩C⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠, C⎛⎝(αP₁)/(N₁)⎞⎠⎫⎭C^* = max_{0 ≤ α ≤ 1}min⎧⎩C⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠, C⎛⎝(αP₁)/(N₁)⎞⎠⎫⎭C^* = max_{0 ≤ α ≤ 1}min⎧⎩C⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠, C⎛⎝(αP₁)/(N₁)⎞⎠⎫⎭

where α = (1 − α) and:

C(X) = (1)/(2)⋅log(1 + x) x ≥ 0

Најдобра анализа од која потоа оваа лесно се конта е онаа за multi-access channel од EIT Chapter 15.3.6

1) If

(P₂)/(N₂) ≥ (P₁)/(N₁)

it can be seen that C^* = C⎛⎝(P₁)/(N₁)⎞⎠(This is achieved by α = 1). The channel appears to be noise free after the relay, an the capacity C⎛⎝(P₁)/(N₁)⎞⎠ from the x₁ to the relay can be achieved. Thus the rate without the relay C⎛⎝(P₁)/(N₁ + N₂)⎞⎠ is increased by the relay to C⎛⎝(P₁)/(N₁)⎞⎠. For large N₂, and for \strikeout off\uuline off\uwave off(P₂)/(N₂) ≥ (P₁)/(N₁) we see that the increment in rate is from C⎛⎝(P₁)/(N₁ + N₂)⎞⎠\thickapprox0 to C⎛⎝(P₁)/(N₁)⎞⎠.

2) For (P₂)/(N₂) < (P₁)/(N₁), it can be seen that the maximizing α = α^* is strictly less that one, and is given by solving for α in:

ln⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠ = ln⎛⎝1 + (αP₁)/(N₁)⎞⎠

yielding C^* = C⎛⎝α^*(P₁)/(N₁)⎞⎠.

\undersetfln⎛⎝1 + (P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠ = \undersetgln⎛⎝1 + (αP₁)/(N₁)⎞⎠
(N₁P₂)/(N₂) < P₁ P₂ < (N₂P₁)/(N₁)
(P₁ + P₂ + 2⋅√(αP₁P₂))/(N) = 1 + (αP₁)/(N) (P₁ + P₂ + 2⋅√(αP₁P₂))/(N) = (P₁ + P₂)/(N₁ + N₂) + (2√((1 − α)P₂P₁))/(N₁ + N₂) < (P₁ + (N₂P₁)/(N₁))/(N₁ + N₂) + (2√((1 − α)P₁(N₂P₁)/(N₁)))/(N₁ + N₂) = ((\cancel(N₁ + N₂)P₁)/(N₁))/(\cancelN₁ + N₂) + (2P₁√((1 − α)(N₂)/(N₁)))/(N₁ + N₂) = (P₁)/(N₁) + (2P₁)/(N₁ + N₂)√((1 − α)(N₂)/(N₁))
|α = 0| ≤ (P₁)/(N₁) + (2P₁)/(N₁ + N₂)√((N₂)/(N₁))
Нешто се мотав ама овде не баш сваќам што сака да каже.
Еве сега при пофторното читањена PhD да го пререшам
ln⎛⎝1 + (P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠ = ln⎛⎝1 + (αP₁)/(N₁)⎞⎠
(P₁ + P₂ + 2⋅√(αP₁P₂))/(N) = 1 + (αP₁)/(N) → Maple → \mathnormal[(P₁ − P₂ − N + 2 √(P₂N))/(P₁),(P₁ − P₂ − N − 2 √(P₂N))/(P₁)], [1-(P₂ + N − 2 √(P₂N))/(P₁),1-(P₂ + N + 2 √(P₂N))/(P₁)]

First we sketch the achievability of C^* and the random code that achieves it. For 0 ≤ α ≤ 1 let \mathchoiceX₂ ~ N(0, P₂)X₂ ~ N(0, P₂)X₂ ~ N(0, P₂)X₂ ~ N(0, P₂), \mathchoiceX₁₀ ~ N(0, αP₁)X₁₀ ~ N(0, αP₁)X₁₀ ~ N(0, αP₁)X₁₀ ~ N(0, αP₁), with X₁₀, X₂ independent, and let

\mathchoiceX₁ = √(α⋅(P₁)/(P₂))X₂ + X₁₀X₁ = √(α⋅(P₁)/(P₂))X₂ + X₁₀X₁ = √(α⋅(P₁)/(P₂))X₂ + X₁₀X₁ = √(α⋅(P₁)/(P₂))X₂ + X₁₀. Then referring to Theorem 1, we evaluate:

I(X₁, X₂;Y) = ln⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠

I(X₁;Y₁|X₂) = (1)/(2)⋅ln⎛⎝1 + (αP₁)/(N)⎞⎠

************************************************************************************************
X₁ = √(α⋅(P₁)/(P₂))X₂ + X₁₀
EX²₁ = αP₁ + αP₁ = P₁
X₂ ~ N(0, P₂), X₁₀ ~ N(0, αP₁)
y_1i = x_1i + z_1i
y_i = x_2i + y_1i + z_i = x_2i + x_1i + z_1i + z_i
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = H(X₂ + Y₁ + Z) − H(X₂ + Y₁ + Z|X₁X₂) =
= H(X₂ + X₁ + Z₁ + Z) − H(X₂ + X₁ + Z₁ + Z|X₁X₂) = (1)/(2)log(P₂ + P₁ + N₁ + N₂) − (1)/(2)log(N₁ + N₂) = (1)/(2)log(P₁ + P₂ + N₁ + N₂)/(N₁ + N₂) =
(1)/(2)log⎛⎝1 + (P₁ + P₂)/(N₁ + N₂)⎞⎠ = C⎛⎝1 + (P₁ + P₂)/(N₁ + N₂)⎞⎠
I(X₁;Y₁|X₂) = H(X₁ + Z₁|X₂) − H(X₁ + Z₁|X₁X₂) =
= H(X₁ + Z₁) − H(Z₁) = (1)/(2)log(P₁ + N₁) − (1)/(2)log(N₁) = (1)/(2)log(P₁ + N₁)/(N₁ + N₂) =
(1)/(2)log⎛⎝1 + (P₁)/(N₁)⎞⎠ = C⎛⎝(P₁)/(N₁)⎞⎠
Ако земеш P₁ = αP₁ следи
I(X₁;Y₁|X₂) = C⎛⎝(αP₁)/(N₁)⎞⎠
***********************************************************************************************
Вака резонирам. Со оглед на тоа што I(X₁;Y₁|X₂) е информацијата што се пренесува во претходниот тајмслот према релето тогаш снагата на X₁ = X₁₀
————————————————————
Потсетување од EIT Chapter 15.3.3
I(X₂;Y|X₁) = H(X₂|X₁) − H(X₂|Y, X₁) = H(X₂) − H(X₂|Y, X₁) = I(X₂;Y, X₁) = I(X₂;Y) + I(X₂;X₁|Y) ≥ I(X₂;Y)
————————————————————–
\mathchoiceI(X₁;Y₁|X₂)I(X₁;Y₁|X₂)I(X₁;Y₁|X₂)I(X₁;Y₁|X₂) = H(X₁ + Z₁|X₂) − H(X₁ + Z₁|X₁X₂) =
= H(X₁₀ + Z₁) − H(Z₁) = (1)/(2)log(αP₁ + N₁) − (1)/(2)log(N₁) = (1)/(2)log(P₁ + N₁)/(N₁) = (1)/(2)log⎛⎝1 + (αP₁)/(N₁)⎞⎠ = \mathchoiceC⎛⎝(αP₁)/(N₁)⎞⎠C⎛⎝(αP₁)/(N₁)⎞⎠C⎛⎝(αP₁)/(N₁)⎞⎠C⎛⎝(αP₁)/(N₁)⎞⎠
I(X₁;Y₁|X₂) + I(X₂;Y) =
I(X₁X₂;Y) = I(X₂;Y) + I(X₁;Y|X₂) = I(X₂;Y) + H(Y|X₂) − H(Y|X₁X₂)
I(X₁;Y|X₂) = H(Y|X₂) − H(Y|X₁X₂) ≤ H(Y|X₂) − H(Y|X₁X₂Y₁) = (*)
H(Y|X₁X₂Y₁) = H(Y|X₂Y₁)
(*) = H(Y|X₂) − H(Y|X₂Y₁) = I(X₂;Y|Y₁) ≤ I(Y₁;Y) + I(X₂;Y|Y₁) = I(X₂Y₁;Y)
For degraded channel we have:
X₁ → (X₂, Y₁) → Y
I(X₁;X₂Y₁) ≥ I(X₁;Y)
\overset0I(X₁;X₂) + I(X₁;Y₁|X₂) ≥ I(X₁;Y) → \mathchoiceI(X₁;Y₁|X₂) ≥ I(X₁;Y)I(X₁;Y₁|X₂) ≥ I(X₁;Y)I(X₁;Y₁|X₂) ≥ I(X₁;Y)I(X₁;Y₁|X₂) ≥ I(X₁;Y)
************************************************************************************************
I(X₁, X₂;Y) = ln⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠
E(X²₂) = P₂((1 − √(α)))/((1 + √(α)))
y_1i = x_1i + z_1i
y_i = x_2i + y_1i + z_i = x_2i + x_1i + z_1i + z_i
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = H(X₂ + Y₁ + Z) − H(X₂ + Y₁ + Z|X₁X₂) =
= H(X₂ + X₁ + Z₁ + Z) − H(X₂ + X₁ + Z₁ + Z|X₁X₂) = (1)/(2)log⎛⎝P₂((1 − √(α)))/((1 + √(α))) + P₁ + N₁ + N₂⎞⎠ − (1)/(2)log(N₁ + N₂) = (1)/(2)log(P₁ + P₂ + N₁ + N₂)/(N₁ + N₂) =
****************************************************************************************************

The assertion that this distribution p(x₁, x₂) actually maximizes min{I(X₁;Y₁|X₂), I(X₁, X₂;Y)} will follow from the proof of the converse.

The random codebook (Section II) associated with this distribution is then given by a random choice of:

X₁̃(w) i.i.d. ~ N_n(0, αP₁I) w ∈ [1, 2^nR]

X₂̃(s) i.i.d. ~ N_n(0, P₂I) w ∈ [1, 2^nR₀]

\mathchoiceR₀ = (1)/(2)log⎛⎝1 + ((√(P₂) + √(αP₁))²)/((αP₁ + N))⎞⎠ − ϵ, R₀ = (1)/(2)log⎛⎝1 + ((√(P₂) + √(αP₁))²)/((αP₁ + N))⎞⎠ − ϵ, R₀ = (1)/(2)log⎛⎝1 + ((√(P₂) + √(αP₁))²)/((αP₁ + N))⎞⎠ − ϵ, R₀ = (1)/(2)log⎛⎝1 + ((√(P₂) + √(αP₁))²)/((αP₁ + N))⎞⎠ − ϵ, and N_n(0, I) denotes the n-variate normal distribution with identity co variance matrix I. The code book is given by

Немам идеја од каде го добива овој израз за R₀. Претпоставувам нешто со пресметка на матрицата на коварианси. Ама како изгледа таа:

x₁(w|s) = x₁̃(w) + √((αP₁)/(P₂))x₂(s)

x₂(s), w ∈ [1, 2^nR] s ∈ [1, 2^nR₀].

The codewords so generated (1 − ϵ)-satisfy the power constraints with high probability, and thus the overall average probability of error can be shown to be small.

Ова се неуспешните обиди да го најдам R₀. Решението е во наредниот box.
I(X₁, X₂;Y) = ln⎛⎝(P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠

\strikeout off\uuline off\uwave offR₀ = (1)/(2)log⎛⎝1 + ((√(P₂) + √(αP₁))²)/((αP₁ + N))⎞⎠ − ϵ

\strikeout off\uuline off\uwave offX₁ = √(α⋅(P₁)/(P₂))⋅X₂ + X₁₀

R₀ ≤ I(X₂;Y) = H(X₂) − H(X₂|Y)
R₀ ≤ (1)/(2)log(2πe)⋅(σ²_x₂ + σ²_Z₂) − (1)/(2)log(2πe)⋅(σ²_Z₂) = (1)/(2)log(2πe)⋅(1 + (σ²_x₂)/(σ²_Z₂))
X₂ = √((P₂)/(αP₁))(X₁ − X₁₀) E(X²₂) = (P₂)/(αP₁)⋅E((X₁ − X₁₀)²) ≤ P₂
********************************************************************************
20.06.14
E((X₁ − X₁₀)²) = E(X²₁) − 2E(X₁X₁₀) + E(X²₀) = P²₁ − 2P₁αP₁ + α²P²₁
(P₂)/(αP₁)(P₁ − 2√(P₁)√(αP₁) + αP₁) = ⎛⎝(P₂)/(1 − α) − (2√(α))/((1 − α))P₂ + (α)/((1 − α))⋅P₂⎞⎠ = (P₂ − 2√(α)P₂ + αP₁)/((1 − α)) = (P₂ − 2√(α)P₂ + αP₂)/((1 − α)) = P₂((1 − √(α))²)/(1 − α) = P₂((1 − √(α))^\cancel2)/(\cancel(1 − √(α))(1 + √(α))) = P₂((1 − √(α)))/((1 + √(α)))
E(X²₁) = E(√(α⋅(P₁)/(P₂))⋅X₂ + X₁₀)² = P₁ + 2√(α⋅(P₁)/(\cancelP₂))√(\cancelP₂)√(αP1) + αP₁ = P₁ + 2√(ααP₁P₁) + αP₁
Y = X₁̂ + X₂ E(X₁̂²) = αP₁
I(X₁, X₂;Y) = H(Y) − H(Y|X₁X₂) = H(X₂ + X₁ + Z) − H(X₂ + X₁ + Z|X₁X₂) =
= H(X₂ + X₁ + Z₁ + Z) − H(Z₁ + Z|X₁X₂) = (1)/(2)log(E(X₁ + X₂)² + N₁ + N₂) − (1)/(2)log(N₁ + N₂) = (*)
E(X₁ + X₂)² = αP₁ + 2√(P₁αP₂) + P₂
(*) = (1)/(2)log⎛⎝1 + (αP₁ + 2√(P₁αP₂) + P₂)/(N₁ + N₂)⎞⎠
**********************************************************************************
08.10.2014 (Овде више ги сменив ознаките во докторатот и се прилагодив на ознаките во NIT на El Gammal
Y₃ = X₂ + Y₂ + Z₃ = X₂ + X₁ + Z₂ + Z₃
R₀ = I(X₂;Y₃) = (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]) − (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]|X₂) = (1)/(2)⋅log(P₂ + E(Y²₂) + N₃) − (1)/(2)⋅log(E(Y²₂) + N₃)
Изгледа зема Y₂ ~ X₁₀ ~ N(0, αP₁) и претпоставува дека X₂ е корелирано со Y₂
R₀ = I(X₂;Y₃) = (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]) − (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]|X₂) = (1)/(2)⋅log(Var[X₂ + X₁₀ + Z₂] + N₃) − (1)/(2)⋅log(Var[αP₁ + Z₂ + Z₃]) =
= (1)/(2)⋅log(Var[X₂ + X₁₀] + N₂ + N₃) − (1)/(2)⋅log(Var[X₁₀] + N₂ + N₃) = (1)/(2)⋅log(Var[X₂ + X₁₀] + N) − (1)/(2)⋅log(Var[X₁₀] + N) =
X₁ = √(α⋅(P₁)/(P₂))⋅X₂ + X₁₀ → X₁₀ = X₁ − √(α⋅(P₁)/(P₂))⋅X₂ → X₂ = √((P₂)/(αP₁))⋅(X₁ − X₁₀)
E[X²₁] = (√(α⋅(P₁)/(P₂)))²⋅E[X²₂] + αP₁ = α⋅(P₁)/(P₂)⋅P₂ + αP₁ = α⋅P₁⋅ + αP₁ = P₁

Var[X₂ + X₁] = Var[X₂ + √(α⋅(P₁)/(P₂))⋅X₂ + X₁₀] = P₂ + (1 − α)P₁ + αP₁ = P₂ + P₁
Var[X₂ + X₁] = P₂ + 2⋅E[X₁X₂] + P₁ = P₂ + 2⋅E[(√(α⋅(P₁)/(P₂))⋅X₂ + X₁₀)X₂] + P₁ = P₂ + 2⋅E[√(α⋅(P₁)/(P₂))⋅X²₂ + X₁₀X₂] + P₁ = P₂ + 2⋅P₂ + 2⋅E[X₁₀X₂] + P₁ =
= P₂ + 2⋅P₂ + 2⋅αP₁P₂ + P₁ = P₂ + 2⋅P₂ + 2⋅(1 − α)P₁P₂ + P₁
(√(P₂) + √(αP₁))² = P₂ + 2√(αP₁P₂) + αP₁

Var[X₂ + X₁₀] = P₂ + 2⋅E[X₁₀X₂] + P₁ = P₂ + 2E[(X₁ − √(α⋅(P₁)/(P₂))⋅X₂)⋅X₂] + P₁ = P₂ + 2⋅E[X₁X₂ − √(α⋅(P₁)/(P₂))⋅X₂⋅X₂] + P₁ = P₂ + 2√(P₁)√(P₂) − (1 − α)P₁ + P₁ = P₂ + 2P₁P₂ + αP₁

= P₂ + 2P₁P₂ + (1 − α)P₁ = P₂ + 2P₁P₂ + P₁ − αP₁ + αP₁ − αP₁ = αP₁ + P₂ + 2P₁P₂ + P₁ − \cancelαP₁ − (1 − \cancelα)P₁

(1)/(2)⋅log(Var[X₂ + X₁₀] + N) − (1)/(2)⋅log(Var[X₁₀] + N) = (1)/(2)⋅log(Var[X₂] + Var[X₁₀] + N) − (1)/(2)⋅log(Var[X₁₀] + N) = (1)/(2)⋅log⎛⎝(Var[X₂])/(Var[X₁₀] + N) + 1⎞⎠ =

= (1)/(2)⋅log⎛⎝(Var[X₂])/(αP₁ + N) + 1⎞⎠ X₂ = √((P₂)/(αP₁))⋅(X₁ − X₁₀) Var[X₂] = (P₂)/(αP₁)⋅(P₁ − 2⋅E[X₁₀X₁] + αP₁) = (P₂)/(αP₁)⋅(P₁ − 2⋅E[α⋅X₁X₁] + αP₁) = (P₂)/(αP₁)⋅(P₁ − 2⋅α⋅P₁ + αP₁) = P₂

Y₃ = X₂ + Y₂ + Z₃ = X₂ + X₁ + Z₂ + Z₃
X₁ = √(α⋅(P₁)/(P₂))⋅X₂ + X₁₀ → X₁₀ = X₁ − √(α⋅(P₁)/(P₂))⋅X₂ → X₂ = √((P₂)/(αP₁))⋅(X₁ − X₁₀)
R₀ = I(X₂;Y₃) = (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]) − (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]|X₂) = (1)/(2)⋅log(Var[X₂ + X₁₀ + Z₂] + N₃) − (1)/(2)⋅log(Var[αP₁ + Z₂ + Z₃]) =
= (1)/(2)⋅log(Var[X₂ + X₁₀] + N₂ + N₃) − (1)/(2)⋅log(Var[X₁₀] + N₂ + N₃) = (1)/(2)⋅log(Var[X₂ + X₁₀] + N) − (1)/(2)⋅log(αP₁ + N) =
Кога не би биле корелирани
R₀ = (1)/(2)⋅log(P₂ + αP₁ + N) − (1)/(2)⋅log(αP₁ + N) = (1)/(2)⋅log⎛⎝(P₂)/((αP₁ + N)) + 1⎞⎠
Ако се корелирани (а во чланакот велат дека не се) се добива:

Var[X₂ + X₁₀] = P₂ + 2⋅E[X₁₀X₂] + P₁ = P₂ + 2E[(X₁ − √(α⋅(P₁)/(P₂))⋅X₂)⋅X₂] + P₁ = P₂ + 2⋅E[X₁X₂ − √(α⋅(P₁)/(P₂))⋅X₂⋅X₂] + P₁ = P₂ + 2√(P₁)√(P₂) − (1 − α)P₁ + P₁ = P₂ + 2√(P₁)√(P₂) + αP₁

R₀ = (1)/(2)⋅log(P₂ + 2√(P₁)√(P₂) + αP₁ + N) − (1)/(2)⋅log(αP₁ + N) = (1)/(2)⋅log⎛⎝(P₂ + 2√(P₁)√(P₂))/((αP₁ + N)) + 1⎞⎠

X₁ = √(α⋅(P₁)/(P₂))⋅X₂ + X₁₀ → X₁₀ = X₁ − √(α⋅(P₁)/(P₂))⋅X₂ → X₂ = √((P₂)/(αP₁))⋅(X₁ − X₁₀)

R₀ = I(X₂;Y₃) = (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]) − (1)/(2)⋅log(Var[X₂ + Y₂ + Z₃]|X₂) = (1)/(2)⋅log(Var[X₂ + X₁ + Z₂ + Z₃]) − (1)/(2)⋅log(Var[X₁ + Z₂ + Z₃]|X₂) =

= (1)/(2)⋅log(Var[X₂ + X₁] + N) − (1)/(2)⋅log(E_x₂{Var[X₁|X₂]} + N)

\mathchoiceE_x₂{Var[X₁|X₂]}E_x₂{Var[X₁|X₂]}E_x₂{Var[X₁|X₂]}E_x₂{Var[X₁|X₂]} = E[X²₁] − (E[X₁X₂])/(E[X²₂]) = P₁ − (E²[(√(α⋅(P₁)/(P₂))⋅X₂ + X₁₀)X₂])/(P₂) = P₁ − (E²[√(α⋅(P₁)/(P₂))⋅X²₂] + \cancelto0E[X₁₀X₂])/(P₂) = P₁ − (α(P₁)/(P₂)⋅P²₂)/(P₂) = P₁ − (αP₁⋅P₂)/(P₂) = P₁ − αP₁ = \mathchoiceαP₁αP₁αP₁αP₁

Гледаш сега од каде излегува αP₁!!!

R₀ = (1)/(2)⋅log(Var[X₂ + X₁] + N) − (1)/(2)⋅log(αP₁ + N) = (1)/(2)⋅log((Var[X₂ + X₁] + N))/(αP₁ + N)

Var[X₂ + X₁] = P₂ + 2⋅E[X₁X₂] + P₁ = P₂ + 2⋅E[(√(α⋅(P₁)/(P₂))⋅X₂ + X₁₀)X₂] + P₁ = P₂ + 2⋅E[√(α⋅(P₁)/(P₂))⋅X²₂ + X₁₀X₂] + P₁ = P₂ + 2⋅√(α⋅(P₁)/(P₂))⋅P₂ + 2⋅\cancelto0E[X₁₀X₂] + P₁ =

P₂ + 2⋅√(α⋅P₁P₂) + P₁ = P₂ + 2⋅√(α⋅P₁P₂) + αP₁ + αP₁

R₀ = (1)/(2)⋅log((P₂ + 2⋅√(α⋅P₁P₂) + αP₁ + αP₁ + N))/(αP₁ + N) = (1)/(2)⋅log⎛⎝1 + ((P₂ + 2⋅√(α⋅P₁P₂) + αP₁))/(αP₁ + N)⎞⎠ = (1)/(2)⋅log⎛⎝1 + ((√(P₂) + √(αP₁))²)/(αP₁ + N)⎞⎠

(√(P₂) + √(αP₁))² = P₂ + 2√(αP₁P₂) + αP₁

Q.E.D!!!

Now the converse. Any code for the channel specifies a joint probability distribution W, X₁, X₂, Y₁, Y.

nR ≤ ⁿ⎲⎳_i = 1I(X_1i;Y_1i, Y_i|X_2i) + nδ_n = ⁿ⎲⎳_i = 1I(X_1i;Y_1i|X_2i) + nδ_n

From corollary 1:I(X₁;Y, Y₁|X₂) = I(X₁;Y₁|X₂)

by degradedness. Thus

nR ≤ ⁿ⎲⎳_i = 1[H(Y_1i|X_2i) − H(Y_1i|X_2i, X_1i)] + nδ_n = ⁿ⎲⎳_i = 1[H(Y_1i|X_2i) − H(X_1i + Z_1i|X_2i, X_1i)] + nδ_n

= ⁿ⎲⎳_i = 1[H(Y_1i|X_2i) − ⁿ⎲⎳_j = 1p(X_1i = x_1j)H(x_1j + Z_1i|X_2i, X_1i = x_1j)] + nδ_n = ⁿ⎲⎳_i = 1[H(Y_1i|X_2i) − H(Z_1i|X_2i)] + nδ_n =

Now for any i:

(56) H(Y_1i|X_2i) = E[H(Y_1i|x_2i] ≤ E⎡⎣(1)/(2)log(var(Y_1i|x_2i))⎤⎦ ≤ (1)/(2)log(E[var(Y_1i|x_2i)])

Y_1i = X_1i + Z_1i then

where E[var(X_1i|X_2i)] = A_i, i = 1..n . Substituting in 55↑ we have:

(57) R ≤ (1)/(n)ⁿ⎲⎳_i = 1(1)/(2)log2πe(A_i + N₁) − (1)/(2)⋅log((2πe)N₁) + δ_n = (1)/(2)⋅(1)/(n)ⁿ⎲⎳_i = 1log⎛⎝(A_i)/(N₁) + 1⎞⎠ ≤ (1)/(2)⋅log⎛⎝1 + (\mathchoice(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i)/(N₁)⎞⎠ + δ_n

again by Jensen’s inequality. However

\mathchoice(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i(1)/(n)ⁿ⎲⎳_i = 1A_i = (1)/(n)ⁿ⎲⎳_i = 1(E(X²_1i) − E(E²(X₁|X_2i))) ≤ P₁ − \mathchoice(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)

A_i = E_x₂[var(X_1i|X_2i)] = E_X₂(E_X₁(X²_1i|X_2i) − E²_X₁(X_1i|X_2i)) = E_X₁(X²_1i) − E_X₂E²_X₁(X_1i|X_2i)
Ова следи од total Expectation theorem.

by the power constraint on the code book.

Define:

(58) αP₁ = \mathchoice(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i)(1)/(n)ⁿ⎲⎳_i = 1EE²(X_1i|X_2i), α ∈ [0, 1]

Thus 57↑ becomes

R ≤ (1)/(2)⋅ln2πe⎛⎝1 + (P₁ − αP1)/(N₁)⎞⎠ + δ_n = (1)/(2)⋅ln2πe⎛⎝1 + (P₁ − (1 − α)P₁)/(N₁)⎞⎠ + δ_n = (1)/(2)⋅ln2πe⎛⎝1 + (αP₁)/(N₁)⎞⎠ + δ_n.

Многу убави и елегантни работи има во овој доказ! Би рекол дека се работи за суштински изведувања!!!

\strikeout off\uuline off\uwave off

y_1i = x_1i + z_1i

y_i = x_2i + y_1i + z_i

nR ≤ ⁿ⎲⎳_i = 1I(X_1i, X_2i;Y_i) + nδ_n ≤ ⁿ⎲⎳_i = 1[H(Y_i) − H(Y_i|X_1iX_2i)] + nδ_n = ⁿ⎲⎳_i = 1[H(X_2i + Y_1i + Z_i) − H(X_2i + Y_1i + Z_i|X_1iX_2i)] + nδ_n =

ⁿ⎲⎳_i = 1[H(X_2i + Y_1i + Z_i) − H(X_2i + X_1i + Z_1i + Z_i|X_1iX_2i)] + nδ_n = ⁿ⎲⎳_i = 1[H(X_2i + Y_1i + Z_i) − H(Z_1i + Z_i)] + nδ_n =

ⁿ⎲⎳_i = 1⎡⎣H(X_2i + Y_1i + Z_i) − (1)/(2)log(2πe)\oversetN(N₁ + N₂)⎤⎦ + nδ_n = ⁿ⎲⎳_i = 1⎡⎣H(X_2i + X_1i + Z_1i + Z_i) − (1)/(2)log(2πe)N⎤⎦ + nδ_n =

for any i,

(59) H(X_2i + X_1i + Z_1i + Z_i) ≤ (1)/(2)ln(E(X_1i + X_2i)² + N)

Hence

\mathchoiceRRRR ≤ (1)/(n)⋅ⁿ⎲⎳_i = 1(1)/(2)ln2πe(E(X_1i + X_2i)² + N) − (1)/(2)log(2πe)N = (1)/(n)⋅ⁿ⎲⎳_i = 1(1)/(2)ln⎛⎝1 + (E(X_1i + X_2i)²)/(N)⎞⎠ + δ_n ≤

≤ (1)/(2)ln⎛⎝1 + (\mathchoice(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²)/(N)⎞⎠ + δ_n.

Now:

(60) (1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)² = (1)/(n)ⁿ⎲⎳_i = 1E(X²_1i) + (2)/(n)ⁿ⎲⎳_i = 1E(X_1iX_2i) + (1)/(n)ⁿ⎲⎳_i = 1E(X²_2i) ≤ P₁ + P₂ + (2)/(n)ⁿ⎲⎳_i = 1E[X_2i⋅E[X_1i|X_2i]]

E_X₁X₂(X₁X₂) = |p(x₁x₂) = p(x₂)⋅p(x₁|x₂)| = ∫^∞_− ∞∫^∞_− ∞x₁x₂p(x₂)⋅p(x₁|x₂)dx₁dx₂ = ∫^∞_− ∞x₂p(x₂)(\oversetE_X₁[X₁|X₂]∫^∞_− ∞x₁⋅p(x₁|x₂)dx₁)dx₂
= E_X₂[X₂⋅E_X₁[X₁|X₂]] = E[X₂⋅E[X₁|X₂]] ≤
√(∫^∞_− ∞\mathchoicex²₂x²₂x²₂x²₂⋅p(x₂)dx₂⋅∫^∞_− ∞\mathchoice(∫^∞_− ∞x₁p(x₁|x₂)dx₁)²(∫^∞_− ∞x₁p(x₁|x₂)dx₁)²(∫^∞_− ∞x₁p(x₁|x₂)dx₁)²(∫^∞_− ∞x₁p(x₁|x₂)dx₁)²p(x₂)dx₂) = √(E[X²₂]⋅E{E²[X_1i|X_2i]})
|∫_ℜⁿf(x)⋅g(x)dx|² ≤ ∫_Rⁿ\mathchoice|f(x)|²|f(x)|²|f(x)|²|f(x)|²dx⋅∫_Rⁿ\mathchoice|g(x)|²|g(x)|²|g(x)|²|g(x)|²dx

Applying the Cauchy Schwartz inequality to each term in the sum in 60↑, we obtain

The Cauchy-Schwattz inequality states that for all vectors x and y of an inner product space it is true that
|⟨x, y⟩|² ≤ ⟨x, x⟩⋅⟨y, y⟩ |⟨x, y⟩| ≤ ∥x∥⋅∥y∥;
In Euclidean space ℜⁿ with the standard inner product the Cauchy-Schwartz inequality is:
(∑ⁿ_i = 1x_iy_i)² ≤ (∑ⁿ_i = 1x²_i)⋅(∑ⁿ_i = 1y²_i)
(⟨⟨a, b⟩, ⟨c, d⟩⟩²) = = (ac + bd)² = a²c² + 2acbd + b²d² ≤ (a² + b²)⋅(c² + d²) = a²c² + a²d² + b²c² + b²d²
For the inner product space of square-integrable compex-valued functions, one has
|∫_ℜⁿf(x)⋅g(x)dx|² ≤ ∫_Rⁿ|f(x)|²dx⋅∫_Rⁿ|g(x)|²dx
-Апликација на шварцовото неравенство во теорија на веројатност:
In fact we can define an inner product on the set of random variables using the expectation of their product:
\mathchoice⟨X, Y⟩≜E(XY)⟨X, Y⟩≜E(XY)⟨X, Y⟩≜E(XY)⟨X, Y⟩≜E(XY)
And so the cauchy-Schwartz inequality,
|E(XY)|² ≤ E(X²)E(Y²)
Moreover, if μ = E(X) and ν = E(Y), then
|Cov(X, Y)|² = |E((X − μ)(Y − ν))|² = |⟨X-μ, Y − ν⟩|² ≤ ⟨X-μ, X − ν⟩⟨X-μ, Y − ν⟩ = E((X − μ)²)E((Y − ν)²) = Var(X)⋅Var(Y)
Значи коваријансата е помала од производот на поединечните варијанси на случајните променливи.
\mathchoice|Cov(X, Y)|² ≤ Var(X)⋅Var(Y)|Cov(X, Y)|² ≤ Var(X)⋅Var(Y)|Cov(X, Y)|² ≤ Var(X)⋅Var(Y)|Cov(X, Y)|² ≤ Var(X)⋅Var(Y)

\mathchoice(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)²(1)/(n)⋅ⁿ⎲⎳_i = 1E(X_1i + X_2i)² ≤ P₁ + P₂ + \mathchoice(2)/(n)ⁿ⎲⎳_i = 1√(E[X²_2i]⋅E{E²[X_1i|X_2i]})(2)/(n)ⁿ⎲⎳_i = 1√(E[X²_2i]⋅E{E²[X_1i|X_2i]})(2)/(n)ⁿ⎲⎳_i = 1√(E[X²_2i]⋅E{E²[X_1i|X_2i]})(2)/(n)ⁿ⎲⎳_i = 1√(E[X²_2i]⋅E{E²[X_1i|X_2i]})

From 58↑ and the power constraints we know that

ⁿ⎲⎳_i = 1EE²(X_1i|X_2i) = αP₁ (1)/(n)ⁿ⎲⎳_i = 1E[X²_2i] ≤ P₂

Again applying the Cauchy-Schwartz inequality, we have

\mathchoice2ⁿ⎲⎳_i = 1⎛⎝(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2 ≤ √((αP₁)P₂)2ⁿ⎲⎳_i = 1⎛⎝(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2 ≤ √((αP₁)P₂)2ⁿ⎲⎳_i = 1⎛⎝(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2 ≤ √((αP₁)P₂)2ⁿ⎲⎳_i = 1⎛⎝(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2 ≤ √((αP₁)P₂)

Во овој случај се користи класичното Шварцово неравенство:
(∑ⁿ_i = 1x_iy_i)² ≤ (∑ⁿ_i = 1x²_i)⋅(∑ⁿ_i = 1y²_i)²
⎛⎝∑ⁿ_i = 1⎛⎝2⋅(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝2⋅(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2⎞⎠² ≤ ∑ⁿ_i = 1⎛⎝2⋅(E[X²_2i])/(n)⎞⎠∑ⁿ_i = 1⎛⎝2⋅(E{E²[X_1i|X_2i]})/(n)⎞⎠
⎛⎝∑ⁿ_i = 1⎛⎝2⋅(E[X²_2i])/(n)⎞⎠^1 ⁄ 2⎛⎝2⋅(E{E²[X_1i|X_2i]})/(n)⎞⎠^1 ⁄ 2⎞⎠ ≤ √(∑ⁿ_i = 1⎛⎝2⋅(E[X²_2i])/(n)⎞⎠⋅∑ⁿ_i = 1⎛⎝2⋅(E{E²[X_1i|X_2i]})/(n)⎞⎠) = 2⋅√((1)/(n)∑ⁿ_i = 1E[X²_2i]⋅(1)/(n)∑ⁿ_i = 1E{E²[X_1i|X_2i]}) = 2⋅√(P₂(αP₁))

Where the maximum occurs when \strikeout off\uuline off\uwave offE{E²[X_1i|X_2i]} = αP₁ and E[X²_2i] = P₂ for all i. Therefore

(61) R ≤ (1)/(2)⋅ln⎛⎝1 + (P₁ + P₂ + 2⋅√(αP₁P₂))/(N)⎞⎠ + δ_n

Converse follows directly form 58↑ and 61↑.

Suppose we have a relay channel (X₁xX₂, p(y, y₁|x₁x₂), Y₁ Y₂). No degradedness relation between y and y₁ will be assumed. Let there be feedback from (y, y₁) to x₁ and to x₂ as shown in 5↓.

Figure 5 Relay Channel with feedback

to be precise the encoding functions in 2↑ and 3↑ now become

x_1i(w, y₁, y₂..., y_i − 1, y₁₁y₁₂..., y_1i − 1)

(62) x_2i(y₁, y₂, ...y_i − 1, y₁₁, y₁₂, ..., y_1i − 1).

Placing a distribution on w ∈ [1, 2^nR] thus induces the joint probability mass function.

(63) p(w, x₁, x₂, y, y₁) = p(w)ⁿ∏_i = 1p(x_1i|w, y^i − 1, y^i − 1₁)⋅p(x_2i|y^i − 1y^i − 1₁)⋅p(y_i, y_1i|x_1ix_2i)

where y^k = (y₁, y₂, ..., y_k). Theorem 3 states that the capacity C_FB of this channel is:

(64) \mathchoiceC_FB = max_{p(x₁, x₂)}{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}C_FB = max_{p(x₁, x₂)}{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}C_FB = max_{p(x₁, x₂)}{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}C_FB = max_{p(x₁, x₂)}{I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}

The relay channel with feedback is ordinary degraded relay channel under the substitution of (Y, Y₁) for Y₁. Thus the code and proof of the forward part of Theorem 1 apply, yielding the ϵ-achievability of C_FB. For this converse, inspection of the proof of Theorem 4 reveals that all the steps apply to the feedback channel - the crucial step being 50↑. Thus the proof of Theorem 3 is complete.

The code used in Theorem 1 will suffice for the feedback channel. However, this code can be simplified by eliminating the random partitions S, because the relay knows the y sequence through the feedback link. An enumeration encoding for the relay can be used instead[6].

If the channel (X₁xX₂, p(y, y₁|x₁x₂), YxY₁) is degraded or reversely degraded then feedback does not increase the capacity.

If the channel is degraded, then

I(X₁;Y, Y₁|X₂) = I(X₁;Y₁|X₂)

Thus C_FB = C. If the channel is reversely degraded, then

I(X₁;Y, Y₁|X₂) = I(X₁;Y|X₂)

Thus C_FB = C.

We are now in a position to discuss the nature of the capacity region for the general relay channel. First, if we have feedback we know the capacity. Next, we note that the general relay channel will involve the idea of cooperation (for the degraded relay channel) and facilitation (for the reversely degraded relay channel). If y₁ is better than the y, then the relay cooperates to send x₁; if y₁ is worse than y, then the relay facilitates the transmission of x₁ by sending the best x₂. Yet another consideration will undoubtedly be necessary - the idea of sending alternative information. This alternative information about x₁ is not zero, thus precluding simple facilitation, and is not perfect, thus precluding pure cooperation.

Finally, we note that the converse (Theorem 4) yields:

C_general ≤ max_p(x₁x₂){I(X₁, X₂;Y), I(X₁;Y, Y₁|X₂)}

For the general channel. Moreover, the code construction for Theorem 1 shows that

C_general ≥ max_p(x₁x₂){I(X₁, X₂;Y), I(X₁;Y₁|X₂)}

Also, from Theorem 2, we see

C_general ≥ max_p(x₁)max_x₂I(X₁;Y|x₂).

If the relay channel is not degraded, cooperation may not be possible and facilitation can be improved upon. As an example consider the general Gaussian relay channel shown in Fig. 5.

If we assume that \mathchoiceN₁ > NN₁ > NN₁ > NN₁ > N, then cooperation in the sense of Section II cannot be realized, since every (2^nR, n, ϵ) code for y₁ will be a (2^nR, n, ϵ) code for y. However, the relay sequence Y₁ is an „observation” of X₁ that is independent of Y. Thus sending Y₁ to y will decrease the effective noise in the y observation of x₁. If the relay power P₁ is finite, and therefore we cannot sent Y₁ to y precisely, then we send an estimate Ŷ₁ of Y₁.

Мене не ми изгледа дека се испраќа нешто од релето. Можеби треба приемникот да го претпостави Y₁ без релето воопшто да испраќа нешто до приемникот. Дефинитивно е вака. Види го параграфот decoding подолу. Тоа е и во солгасност со номенклатурата на променливите. Во претходната елаборација една „капа” подразбираше приемник, а две „капи” подразбираше реле.

21.06.14
Ŷ₁ ми личи на дефиницијата на естимација во Rate Distortion.

The choice of the estimate Ŷ₁ will be clear in Theorem 6 for the discrete memoryless relay channel. Then in Theorem 7, we shall combine Theorem 1 and 6.

figure General Gaussian relay channel.png

Figure 6 General Gaussian relay channel

Let (X₁xX₂, p(y, y₁|x₁x₂), YxY₁) be any discrete memoryless relay channel. Then the rate R^*₁ is achievable, where

(65) \mathchoiceR^*₁ = supI(X₁;Y, Y₁̂|X₂)R^*₁ = supI(X₁;Y, Y₁̂|X₂)R^*₁ = supI(X₁;Y, Y₁̂|X₂)R^*₁ = supI(X₁;Y, Y₁̂|X₂)

subject to constraint

(66) I(X₂;Y) ≥ I(Y₁;Ŷ₁|X₂, Y)

where the supremum is taken over all joint distributions on (X₁xX₂xYxY₁xŶ₁) of the form:

(67) p(x₁, x₂, y, y₁, ŷ₁) = p(x₁)p(x₂)p(y, y₁|x₁x₂)p(ŷ₁|y₁x₂)

and Ŷ₁ has a finite range.

A block Markov encoding is used. At the end of any block i, the x₂ information is used to resolve the uncertainty of the receiver about w_i − 1.

1) Chose 2^nR₁ i.i.d. \mathnormalx₁ each with probability p(x₁) = ∏ⁿ_i = 1p(x_1i). Label these x₁(w), w ∈ [1, 2^nR₁].

2) Chose 2^nR₀ i.i.d x₂ each with probability p(x₂) = ∏ⁿ_i = 1p(x_2i). Label these x₂(s), s ∈ [1, 2^nR₀].

3) Chose, for each x₂(s), \mathchoice2^nR̂ i.i.d. Ŷ₁2^nR̂ i.i.d. Ŷ₁2^nR̂ i.i.d. Ŷ₁2^nR̂ i.i.d. Ŷ₁ each with probability p(ŷ₁| x₂(s)) = ∏ⁿ_i = 1p(ŷ_1i|x_2i(s)), where, for x₂ ∈ X₂, ŷ₁ ∈ \mathnormalŶ₁, we define

(68) p(ŷ₁|x₂) = ⎲⎳_{x₁, y, y₁}p(x₁)p(y, y₁|x₁x₂)p(ŷ₁|y₁x₂)

\strikeout off\uuline off\uwave off∑_{x₁, y, y₁}p(x₁)p(y, y₁|x₁x₂)p(ŷ₁|y₁x₂) = ∑_y, y₁p(y, y₁|x₂)p(ŷ₁|y₁x₂) = ∑_y, y₁p(y₁|x₂)p(y|y₁x₂)p(ŷ₁|y₁x₂) = ∑_yp(y|y₁x₂)p(ŷ₁|x₂) =

Label these \mathchoiceŷ₁(z|s), s ∈ [1, 2^nR₀], z ∈ [1, 2^nR̂]ŷ₁(z|s), s ∈ [1, 2^nR₀], z ∈ [1, 2^nR̂]ŷ₁(z|s), s ∈ [1, 2^nR₀], z ∈ [1, 2^nR̂]ŷ₁(z|s), s ∈ [1, 2^nR₀], z ∈ [1, 2^nR̂].

z е аналогно на w во Секција II. Јас би рекол дека R̂ е брзината на каналот од изворот до релето!?

4) Randomly partition the set {1, 2, ..., 2^nR̂} into 2^nR₀ cells S_s, s ∈ [1, 2^nR₀].

Let w_i be the message to be sent in block i, and assume that (Ŷ₁(z_i − 1|s_i − 1), Y₁(i − 1), x₂(s_i − 1)) are jointly ϵ-typical, and that Z_i − 1 ∈ S_{s_i}. Then the codeword pair (x₁(w_i), x₂(s_i)) will be transmitted in block i.

At the end of the block i we have the following.

i) The receiver estimates s_i by ŝ_i by looking for the unique typical x₂(s_i) with y(i). If \mathchoiceR₀ ≤ I(X₂;Y)R₀ ≤ I(X₂;Y)R₀ ≤ I(X₂;Y)R₀ ≤ I(X₂;Y) and n is sufficiently large, then this decoding operation will incur small probability of error.

ii) The receiver calculates a set L(y(i − 1)) of z such that z ∈ L(y(i − 1)) if (ŷ₁(z_i − 1|s_i − 1), x₂(s_i − 1), y(i − 1)) are jointly ϵ-typical. The receiver then declares that z_i − 1 was sent in block i − 1 if

ẑ_i − 1 ∈ S_{ŝ_i}∩L(y(i − 1)).

But, from an argument similar to that in Lemma 3, we see that ẑ_i − 1 = z_i − 1 with arbitrarily high probability provided n is sufficiently large and

(69) \mathchoiceR̂ < I(Ŷ₁;Y|X₂) + R₀R̂ < I(Ŷ₁;Y|X₂) + R₀R̂ < I(Ŷ₁;Y|X₂) + R₀R̂ < I(Ŷ₁;Y|X₂) + R₀.

Во овој израз Ŷ₁ многу личи на X₁!?

figure Relationship of auxilary variables.png

Figure 7 Relationship of auxiliary variables

iii) Using both ŷ₁(ẑ_i − 1|ŝ_i − 1) and y(i − 1) the receiver finally declares that ŵ_i − 1 was sent in block i − 1 if (x₁(ŵ_i − 1), ŷ₁(ẑ_i − 1|s_i − 1), y(i − 1), x₂(ŝ_i − 1)) are jointly ϵ-typical. Thus ŵ_i − 1 = w_i − 1 with high probability if

(70) \mathchoiceR₁ < I(X₁;Y, Ŷ₁|X₂)R₁ < I(X₁;Y, Ŷ₁|X₂)R₁ < I(X₁;Y, Ŷ₁|X₂)R₁ < I(X₁;Y, Ŷ₁|X₂)

and sufficiently large n. Овој израз ми е аналоген на оној за degraded channel ако го замислиш (Y, Ŷ₁) дека e всушнос Y₁

iv) The relay, upon receiving y₁(i) decides that z is „received” if (ŷ₁(z|s_i), y₁(i), x₂(x_i)) are jointly ϵ-typical. There will exist such a z with high probability if:

(71) R̂ > I(Ŷ₁;Y₁|X₂)

and n is sufficiently large. (See [10] [11] [12] and especially the proof of Lemma 2.1.3 in [12]).

The decoding error calculations for steps i)-iii) are similar to those in Section II. The decoding error in step iv) follows from the theory of side information in [10] and [11]. Let

R₀ = I(X₂;Y) − ϵ

R̂ = I(Ŷ₁;Y₁|X₂) + ϵ

This together with the constraint in 69↑ collapses to yield

\strikeout off\uuline off\uwave off

I(X₂;Y) ≥ I(Ŷ₁;Y₁|X₂, Y)

\strikeout off\uuline off\uwave off

\strikeout off\uuline off\uwave offR̂ < I(Ŷ₁;Y|X₂) + R₀

Thus we see that the rate R^*₁ given in 65↑ is achievable.

Затоа што поаѓајќи од изразите за брзините на каналот стигаш до ограничувањето 66↑

1) Small values of I(X₂;Y) will constrain Ŷ₁ to be a highly degraded version of Y₁ in order that 66↑ is satisfied. Ова произлегува од I(X₂;Y) ≥ I(Ŷ₁;Y₁|X₂, Y). Ако е мало I(X₂;Y) тогаш \strikeout off\uuline off\uwave offI(Ŷ₁;Y₁|X₂, Y)\uuline default\uwave default е уште помало. Ако е многу мало тогаш Ŷ₁ нема да има врска со Y₁ т.е. ќе биде многу деградирана верзија на Y₁.

2) The reversely degraded relay capacity C₀ is always less than or equal to the achievable rate R^*₁ given in 65↑.

We have seen in Section II that the rate of the channel from X₁ to Y can be increased through cooperation. Alternatively we have claimed in theorem 6 that by transmitting an estimate Ŷ₁ of Y Претпоставувам Y₁ сака да каже!? , the rate can also be increased. The obvious generalization of Theorems 1 and 6 is to superimpose the cooperation and the transmission of Ŷ₁.

Consider the probability structure of 7↑ on VxUxX₁xX₂xYxY₁xŶ₁ where V, U, and ,Ŷ₁ are arbitrary sets. The auxiliary random variables have the following interpretations:

i) V will facilitate cooperation to resolve the residual uncertainty about U.

ii) U will be understood by Y₁ but not by Y. (Informally, U plays the role of X₁ in Theorem 1).

iii) Ŷ₁ is the estimate of Y₁ used in Theorem 6. Ова ми личи на source coding with side information Chapter 15.8.

iv) X₂ is used to resolve Y uncertainty about Y₁.

Finally it can be shown that the following rate is achievable for any relay channel.

For any relay channel (X₁xX₂, p(y, y₁|x₁x₂), YxY₁) the rate R^* is achievable, where

(72) R^* = sup_P{min{I(X₁;Y, Ŷ₁|X₂, U) + I(U;Y₁|X₂, V), I(X₁, X₂;Y) − I(Ŷ₁;Y₁|X₂, X₁, U, Y)}}

where the supremum is taken over all joint probability mass functions of the form

(73) p(u, v, x₁, x₂, y, y₁, ŷ₁) = p(v)p(u|v)p(x₁|u)⋅p(x₂|v)p(y, y₁|x₁x₂)p(ŷ₁|x₂, y₁, u)

subject to constraint

(74) I(Ŷ₁;Y₁|Y, X₂, U) ≤ I(X₂;Y|V)

The forward parts of Theorem 1, 2, and 6 are special cases of R^* in Theorem 7, as the following substitutions show:

1) (Degraded channel, Theorem 1) R^* ≥ C . Chose V ≡ X₂, U ≡ X₁, , and Ŷ₁ ≡ φ

2) (Reversely degraded channel, Theorem 2) R^* ≥ C. Chose V ≡ ∅, U ≡ ∅ , and Ŷ₁ ≡ ∅.

3) (Theorem 6) R^* ≥ R^*₁. Chose V ≡ ∅, U ≡ ∅.

R^* = sup_P{min{I(X₁;Y, Ŷ₁|X₂, U) + I(U;Y₁|X₂, V), I(X₁, X₂;Y) − I(Ŷ₁;Y₁|X₂, X₁, U, Y)}}

1. Chose V ≡ X₂, U ≡ X₁, , and Ŷ₁ ≡ φ

R^* = sup_P{min{I(X₁;Y, Ŷ₁|X₂, X₁) + I(X₁;Y₁|X₂), I(X₁, X₂;Y) − I(∅;Y₁|X₂, X₁, Y)}}
\mathchoiceI(X;Y = ∅) = H(X) − H(X|Y) = H(X) − H(X|∅) = H(X) − H(X) = 0I(X;Y = ∅) = H(X) − H(X|Y) = H(X) − H(X|∅) = H(X) − H(X) = 0I(X;Y = ∅) = H(X) − H(X|Y) = H(X) − H(X|∅) = H(X) − H(X) = 0I(X;Y = ∅) = H(X) − H(X|Y) = H(X) − H(X|∅) = H(X) − H(X) = 0

\strikeout off\uuline off\uwave offI(X₁;Y, Ŷ₁|X₂, X₁) = \cancelto0H(X₁|X₁, X₂) − \cancelto0H(X₁|X₁, X₂, Y, Ŷ₁) = 0

R^* = sup_P{min{I(X₁;Y₁|X₂), I(X₁, X₂;Y)}} навистина ова е Теорема 1

2. Chose V ≡ ∅, U ≡ ∅ , and Ŷ₁ ≡ ∅.

\strikeout off\uuline off\uwave offR^* = sup_P{min{I(X₁;Y|X₂), I(X₁, X₂;Y)}}

3. Chose V ≡ ∅, U ≡ ∅.
R^* = sup_P{min{I(X₁;Y, Ŷ₁|X₂), I(X₁, X₂;Y) − I(Ŷ₁;Y₁|X₂, X₁, Y)}}

As in Theorems 1 and 6, a block Markov encoding scheme is used. At the end of block i, v is used to resolve the uncertainty of y about the past u, and x₂ is used to resolve the y uncertainty about Ŷ₁, thus enabling y to decode w_i − 1.

1) Generate 2^{n(I(V;Y) − ϵ)} i.i.d. v, each with probability p(v) = ∏ⁿ_i = 1p(v_i). Label these v(m), m ∈ [1, 2^{n(I(V, Y) − ϵ)}].

2) For every v(m), generate 2^{n(I(X₂;Y|V) − ϵ)} i.i.d x₂, each with probability

p(x₂|v(m)) = ⁿ∏_i = 1p(x_2i|v_i(m))

Label these x₂(s|m), s ∈ [1, 2^{n(I(X₂;Y|V) − ϵ)}].

3) For every v(m) generate 2^nR₁ i.i.d u each with probability: Како во рандом binning. Големината на кодната азбука ќе биде 2^{n(I(V;Y) − ϵ)}x2^nR₁

p(u|v(m)) = ⁿ∏_i = 1p(u_i|v_i(m)).

Label these \mathchoiceu(w^’|m), w’ ∈ [1, 2^nR₁] u(w^’|m), w’ ∈ [1, 2^nR₁] u(w^’|m), w’ ∈ [1, 2^nR₁] u(w^’|m), w’ ∈ [1, 2^nR₁].

4) For every u(w’|m) generate 2^nR₂ i.i.d. x₁ each with probability

p(x₁|u(w’|m)) = ⁿ∏_i = 1p(x_1i|u_i(w^’|m)).

Label these \mathchoicex₁(w^’’|m, w’), w^’’ ∈ [1, 2^nR₂]x₁(w^’’|m, w’), w^’’ ∈ [1, 2^nR₂]x₁(w^’’|m, w’), w^’’ ∈ [1, 2^nR₂]x₁(w^’’|m, w’), w^’’ ∈ [1, 2^nR₂].

5) For every (x₂(s|m), u(w’|m)), generate 2^{n((Ŷ₁;Y₁|X₂U) + ϵ)} i.i.d. ŷ₁ each with probability

p(ŷ₁|x₂(s|m), u(w’|m)) = ⁿ∏_i = 1p(ŷ_1i|x_2i(s|m), u_i(w’|m))

where, for every x₂ ∈ X₂, u ∈ U , we define

(75) p(ŷ₁|x₂, u) = (⎲⎳_{v, x₁y, y₁}p(v, u, x₁, x₂, y, y₁, ŷ₁))/(⎲⎳_{v, x₁, y, y₁, ŷ₁}p(v, u, x₁, x₂, y, y₁, ŷ₁))

\strikeout off\uuline off\uwave offp(ŷ₁|x₂, u) = (p(u, x₂, ŷ₁))/(p(x₂, u))

and p(v, u, x₁, x₂, y, y₁, ŷ₁) is defined in 73↑. Label these ŷ₁(z|w’, s, m), z ∈ [1, 2^{n(I(Ŷ₁;Y₁|X₂, U) + ϵ)}].

1) Randomly partition the set {1, 2, ..., 2^nR₁} into 2^{n(I(V;Y) − ϵ)} cells S_1m.

2) Randomly partition the set {1, 2, ..., 2^{n(I(Ŷ₁;Y₁|X₂U) + ϵ)}} into \strikeout off\uuline off\uwave off2^{n(I(X₂;Y|V) − ϵ)} cells S_2s.

Let w_i = (w_i’, w_i’’) be the message to be sent in block i, and assume that

(ŷ₁(z_i − 1|w’_i − 1, s_i − 1, m_i − 1), y₁(i − 1), u(w_i − 1’|m_i − 1), x₂(s_i − 1|m_i − 1))

are jointly ϵ-typical and that w_i − 1’ ∈ S_{1m_i} and z_i − 1 ∈ S_{2s_i}. Then the codeword pair (x₁(w_i’’|m_i, w_i’), x₂(s_i|m_i)) will be transmitted in block i.

At the end of block i we have the following.

i) The receiver estimates m_i and s_i, by first looking for the unique ϵ-typical v(m_i) with y(i), then for the unique ϵ-typical x₂(s_i|m_i) with (y(i), v(m_i)). For sufficiently large n this decoding step can be done with arbitrarily small probability of error. Let the estimates of s_i and m_i be ŝ_i, m̂_i respectively.

ii) The receiver calculates a set L₁(y(i − 1)) of w’ such that w’ ∈ L₁(y(i − 1)) if (y(w’|m_i − 1), y(i − 1)) are jointly ϵ-typical. The receiver then declares that ŵ_i − 1 was sent in block i − 1 if:

(76) ŵ_i − 1 ∈ S₁∩L₁(y(i − 1))

From Lemma 3, we see that ŵ_i − 1 = w_i − 1’ with arbitrarily high probability provided n is sufficiently large and:

(77) \mathchoiceR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵ

Не контам од каде го вади овој израз!?
21.06.2013
Треба калсичен доказ на achievability да направиш за да го добиеш. Немам време инаку мислам дека може да се изведе.

Треба да се докаже:

\strikeout off\uuline off\uwave offR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵ

——————————————————————————–——————————————

\strikeout off\uuline off\uwave offp(u, v, x₁, x₂, y, y₁, ŷ₁) = p(v)p(u|v)p(x₁|u)⋅p(x₂|v)p(y, y₁|x₁x₂)p(ŷ₁|x₂, y₁, u)

from 77↑ : R₁ < I(V;Y) + I(U;Y|X₂, V)

R₁ < I(X₁;Y, Ŷ₁|X₂) < I(U;Y, Ŷ₁|X₂) = I(U;Y₁) + I(U;Y|X₂, Y₁)
Потсети се на чланакот на van der Meulen!!!

I(U, X;Y) = I(U;Y) + \cancelto0I(X;Y|U) = I(X;Y) + I(U;Y|X) → \mathchoiceI(U;Y) ≥ I(X;Y)I(U;Y) ≥ I(X;Y)I(U;Y) ≥ I(X;Y)I(U;Y) ≥ I(X;Y) во случај на идеален канал p(x|y)!!!
H(U, f(U) = H(U) + H(f(U)|U) = H(U)
Можеби треба да се оди со претпоставка дека важат маркови ланци!! На пример X₁ не зависи од V ако е даден U.

iii) The receiver calculates a set L₂(y(i − 1)) of z such that z ∈ L₂(y(i − 1)) if (ŷ₁(z|ŵ_i − 1, ŝ_i − 1, m̂_i − 1), x₂(ŝ_i − 1|m̂_i − 1), y(i − 1)) are jointly ϵ-typical. The receiver declares that ẑ_i − 1 was sent in block i − 1 if:

(78) ẑ_i − 1 ∈ S_{2s_i}∩L₂(y(i − 1)).

From [12] we see that ẑ_i − 1 = z_i − 1 with arbitrarily small probability of error if n is sufficiently large and

I(Ŷ₁;Y₁|X₂, U) + ϵ < I(Ŷ₁;Y|X₂, U) + I(X₂;Y|V) − ϵ

(79) I(X₂;Y|V) > I(Ŷ₁;Y₁|X₂, U) − I(Ŷ₁;Y|X₂, U) + 2ϵ.

But since

I(Ŷ₁;Y₁, Y|X₂, U) = I(Ŷ₁;Y₁|X₂, U)

\strikeout off\uuline off\uwave offВеројатно нема неизвесност да го знаеш Ŷ₁ ако го знаеш Y₁.

Then condition 79↑ becomes

I(X₂;Y|V) > I(Ŷ₁;Y₁|Y, X₂, U) + 2ϵ

which as ϵ → 0 gives condition 74↑ in Theorem 7.

iv) Using both ŷ₁(ẑ_i − 1|ŵ_i − 1’, ŝ_i − 1, m̂_i − 1) and y(i − 1), the receiver finally declares that ŵ_i − 1’’ was sent in block i − 1 if \strikeout off\uuline off\uwave off(x₁(ŵ_i − 1’’|ŵ_i − 1’, m̂_i − 1), ŷ₁(ẑ_i − 1|ŵ_i − 1’, ŝ_i − 1, m̂_i − 1), y(i − 1)) are jointly ϵ-typical. ŵ_i − 1’’ = w_i − 1’’ with high probability if

(80) \mathchoiceR₂ = I(X₁;Y, Ŷ₁|X₂, U) − ϵR₂ = I(X₁;Y, Ŷ₁|X₂, U) − ϵR₂ = I(X₁;Y, Ŷ₁|X₂, U) − ϵR₂ = I(X₁;Y, Ŷ₁|X₂, U) − ϵ

\strikeout off\uuline off\uwave offR₁ < I(X₁;Y, Ŷ₁|X₂)

\strikeout off\uuline off\uwave offR₁ < I(V;Y) + I(U;Y|X₂, V) − ϵ

and n is sufficiently large.

figure Fig7 Single sender sinlge receiver network.png

Figure 8 Single sender single receiver network

v) The relay upon receiving y₁(i) declares that w’̂ was received if (u(w’̂|m_i), y₁(i), x₂(s_i|m_i)) are jointly ϵ-typical. w_i’ = ŵ’ with high probability if:

(81) \mathchoiceR₁ < I(U;Y₁|X₂, V)R₁ < I(U;Y₁|X₂, V)R₁ < I(U;Y₁|X₂, V)R₁ < I(U;Y₁|X₂, V)

and n is sufficiently large. Thus, the relay knows that w_i’ ∈ S_{1m_i + 1}.

vi) The relay also estimates z_i such that (ŷ₁(z_i|w_i’, s_i, m_i), y₁(i), x₂(s_i|m_i)) are jointly ϵ-typical. Such a z_i will exist with high probability for large n, therefore the relay knows that z_i ∈ S_{2s_i + 1}.

From 77↑ 78↑ and 81↑, we obtain

R₁ < I(V;Y) + I(U;Y|X₂, V) − ϵ

R₁ < I(U;Y₁|X₂, V)

R₂ = I(X₁;Y, Ŷ₁|X₂, U) − ϵ

.

therefore, the rate of transmission from X₁ to Y is bounded by:

R < I(U;Y₁|X₂, V) + I(X₁;Y, Ŷ₁|X₂, V) − ϵ

ова е првиот член од минимумот во 72↑

Ова е вториот член од минимумот во 72↑

Ова ми изгледа како да зема R = R₁ + R₂;

Substituting from 79↑ we obtain

\strikeout off\uuline off\uwave offI(X₂;Y|V) > I(Ŷ₁;Y₁|X₂, U) − I(Ŷ₁;Y|X₂, U) + 2ϵ

\strikeout off\uuline off\uwave off(a) I(X₂;Y|V) > I(Ŷ₁;Y₁|Y, X₂, U) + 2ϵ

\strikeout off\uuline off\uwave off(b) I(Ŷ₁;Y₁, Y|X₂, U) = I(Ŷ₁;Y₁|X₂, U)

\strikeout off\uuline off\uwave offI(Ŷ₁;Y₁|X₂, U) + ϵ < I(Ŷ₁;Y|X₂, U) + I(X₂;Y|V) − ϵ

\strikeout off\uuline off\uwave offR < I(V;Y) + I(U;Y|X₂, V) + I(X₁;Y, Ŷ₁|X₂, U) − 2ϵ

Во 82↑ имаш \strikeout off\uuline off\uwave offR < I(V;Y) + I(U;Y|X₂, V) + I(X₁;Y, Ŷ₁|X₂, U) − 2ϵ

\strikeout off\uuline off\uwave offR < I(X₂, V;Y) − I(X₁;Ŷ₁|X₂, U, Y) − I(Y₁;Ŷ₁|X₁X₂U, Y) + I(U;Y|X₂, V) + I(X₁;Y, Ŷ₁|X₂, U) − 4ϵ =

\strikeout off\uuline off\uwave offI(X₂, V;Y) + I(U;Y|X₂, V) = I(U, X₂, V;Y)

\strikeout off\uuline off\uwave off = \cancelI(U, X₂;Y) + I(V;Y|U, X₂) + I(X₁, X₂, U;Y) − \cancelI(X₂U;Y) − I(Y₁;Ŷ₁|X₁X₂U, Y) − 4ϵ =

= \cancelto0I(V;Y|U, X₂) + I(U;Y|X₁X₂) + I(X₁, X₂;Y) − I(Y₁;Ŷ₁|X₁, X₂, U, Y) − 4ϵ = I(X₁, X₂;Y) − I(Y₁;Ŷ₁|X₁, X₂, U, Y) − 4ϵ докажано!!!

which establishes Theorem 7.

Theorem 1,2 and 3 establish capacity for degraded, reversely degraded, and feedback relay channels. The full understanding of the relay channel may yield the capacity of the single sender single receiver network in 8↑. This will be the information theoretic generalization of the well known maximum flow-minimum cut theorem [9].

0. Потсети се на achievability of rate од EIT (done)

1. Треба да го поминам [6] за block markovian dependence (не знам дали ова има врска со block markov encoding)

2. Треба да го поминам [7] за random binning proof.
3. Види го доказот на Lemma 2 во [14]

4. Enumeration encoding for the relay [6]

5. Maximum-flow minimum cut theorem [9] (done)

6. G. Kramer, I. Maric and R. D. Yates, Cooperative Communications
7. Откри како го добива R₀ за деградиран Гаусов канал.

Paper- T.Cover, Capacity theorem for the Relay Channels

1 Introduction

2 Achievability of C in Theorems 1,2,3

3 Converse

4 The Gaussian DEGRADED Relay Channel(current)

5 The capacity of the General Relay Channel with Feedback (current)

6 An achievable Rate for the General Relay Channel

7 Concluding Remarks

References

Nomenclature